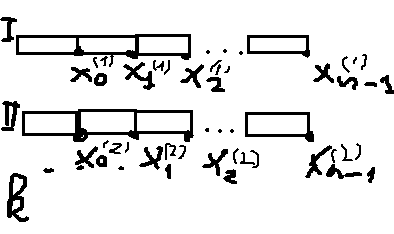
I предприятие II предприятие

ax1+bx₂≤c; gх₃ + hх₄≤k;

dx1+ex₂≤f; lx₃ + mх₄≤n;

ox1 + px₂≤s/2; qх₃ + rx4≤s/2;

tx1 + uх₂ ≤z/2; vx₃ + wх₄≤z/2:

X1>= 0; х₂> =0; xз> 0; x₄> 0;

L1 = (П1x1+ П2x2) max; L2 = (П3хз + П4x₄) max;

3. Эти сведения передаются в объединение, где формируется его план, как механическая сумма планов секторов (предприя­тий), и проверяется оптимальность этого плана.

Необходимонайти такое распределение ресурсов, при котором сумма секторных функционалов будет равна истинному оптимуму. Для этого достаточно, чтобы двойственные оценки одноименного обще­го ресурса в различных секторах были равны между собой.

Оценка 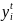показывает приращение прибыли t-й секторной задачи при увеличении количества i-го общего ресурса, выделяемого данному сектору, на 1 ед. (т). Следовательно, секторные оценки общих ресурсов характеризуют эффективность их распределения между пред­приятиями.

• При равенстве оценок эффект от использова­ния ресурсов во всех секторах одинаков и перераспределять их не нужно, т.е. план оптимален.

• Если нет, то распределение ресурсов не оптимально и его можно улучшить перераспределением ресурсов.

Надо перераспределить ресурсы не поровну, а оптимальным способом.

4. Для этого решается новая задача (центральная задача, задача верхнего уровня)

Ищем вектора 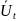(это лимит ресурсов, выделенных предприятию для объединения). Ограничения вектор (вектор лимитов общих ресурсов).

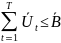
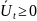
- вектор оценок ресурсов объединения в t- секторе (двойственные оценки!)

Вопрос 12. Индекс Гиттинса последовательности доходов: стохастическая модель со случайными доходами. Экономическая интерпретация.

1. Есть проект, разделенный на несколько этапов:

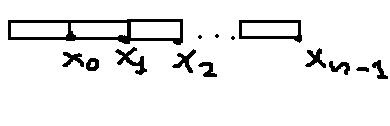Хо – прибыль после выполнения 1го этапа, Х1 – после выполнения 2го этапа, – после выполнения n-го этапа.

Запишем их так – { }

Этапы нельзя менять местами.

2. Есть портфель из проектов.

Задача: в каком порядке выполнять проекты по этапам?

Обозн.

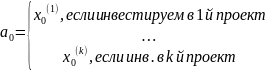
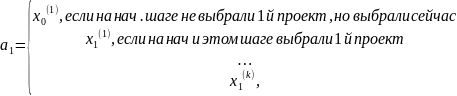
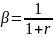, r – ставка %

Тогда критерий эфф-сти:

Или:

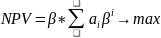
Индекс Гиттинса:

Число проектов конечно тогда

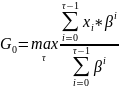
То есть мы максимизируем выручку по 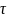после каждого этапа, не забывая о временной стоимости денег.

При = 1 мы получаем X₀.

При = 2 мы получаем .

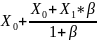При = 3 получим .

И так далее. Мы находим максимальное значение. На каждом шаге надо выполнять тот этап проекта, у к-го максимален индекс.

Экономическая интерпретация – Индекс Гиттинса показывает, сколько денег мы получим, если вы полним этапов (т.е. если равно 1, то 1 этап и т.д.)

Важно вовремя остановиться, поэтому, после нахождения максимального значения мы получаем то максимальное количество денег, которое мы можем получить на проекте, если вовремя остановимся. Если найденный этап не был последний, повторяем все сначала, но за первый теперь берем этап следующий после найденного.

Вопрос 13.Модель компенсированного бюджета. Предпосылки построения. Общий вид модели. Функция Лагранжа. Экономическое содержание множителей Лагранжа.

Модель относится к разделу микроэкономики, описывающему поведение потребителя.

Рассм ситуацию, когда в результате неблагоприятного изменения условий рыночной конъюнктуры, повлекших повышениецен на одно или несколько благ, потребителю необходимо определить денежнуюкомпенсацию к первоначальному бюджетус целью сохранения достигнутого за предыдущие интервалы времени уровня потребительской полезности.

Предполагается, что потребитель полностью осведомлен о состоянии своих потребительских предпочтений и выборов, осуществленных на предыдущих временных интервалах.

Основные предпосылки модели.

1. Потребительский рынок является рынком совершенной конкуренции, т.е. индивидуальный потребитель не может диктовать цены закупаемых благ.

2. Каждый потребитель идентифицируется следующими факторами: - величиной бюджета М, это означает, что, мы рассматриваем потребителя в процессе единомоментного акта потребления товаров, т.е. бюджет расходуется полностью. (Пр.: если, на следующий, день этот же потребитель приходит с другим кошельком (другой суммой денег), то он уже идентифицируется как новый потребитель, тем не менее субъективные отношения сохраняются).

3. Рынок потребительских благ является конечным

• - СФПП (субъективная функция порядковой полезности),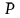

•  вектор рыночных цен на приобретаемые блага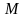

• - размер бюджета потребителя.

• Тогда 

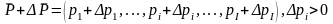
новый вектор цен, соответствующий изменившимся рыночным условиям.

Задача: необходимо определить min размер дополнительной компенсации , на величину которой требуется увеличить первоначальный бюджет потребителя M с целью сохранения его достигнутой ранее потребительской полезности, соответствующей изокванте

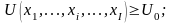
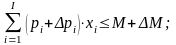
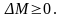
функция Лагранжа:

.

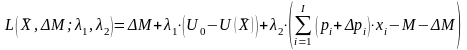Используем условия оптимальности теоремы Куна-Таккера:

;

;

,

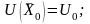
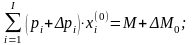
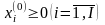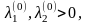где  решение системы уравнений

Условия оптимальности позволяют установить экономическое содержание множителей Лагранжа и .

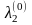• - двойственная оценка 2го ограничения, показывает величину, на которую снизится объем компенсации потребителю в случае, если его первоначальный бюджет увеличится на одну денежную ед. С социально-экономической т.з. этот множитель Лагранжа – есть социальная норма дисконта, т.е. то количество денег, которое гос-во вкладывает в социальную сферу. Это обусловлено тем, что именно государство компенсирует бюджет потребителя при изменении цен.

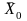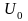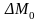• (двойственная оценка 1го ограничения в точке ) характеризует рыночную цену набора благ, приходящуюся на ед. его предельной полезности.Является постоянной для всех благ из набора . Более того, увеличение минимальной общей полезности на одну ед. ведет к увеличению объема дополнительно привлекаемых потребителем бюджетных средств на величину двойственной оценки .