
- •1) Понятие группы, подгруппы, примеры групп.
- •6) Коммутант группы. Критерий коммутативности фактор-группы.
- •7)Нильпотентность конечной р-группы.
- •8)Абелевы группы. Полные абелевы группы.
- •14). Симметрическая группа. Знакопеременная группа.
- •15) Группа невырожденных матриц n-ого порядка и ее подгруппы
- •16) Понятия кольца и поля.
- •17) Алгебра кватернионов
- •19) Круговые многочлены.
- •22) Лемма об отсутствии алгебр с делением размерности 3 над полем вещественных чисел
- •25)Трансцендентные и алгебраические расширения полей
- •26) Теорема о примитивном элементе.
- •27) Булевы алгебры
- •0) Идеалы булевых алгебр и гомоморфизмы
1) Понятие группы, подгруппы, примеры групп.
Пусть
задано некоторое мн-во А,
содержащее особый элемент е,
и на А
задана операция (А, *,е,=), х,у А
А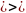 х*у
А
, это мн-во наз-ся группой если: 1)
х*у
А
, это мн-во наз-ся группой если: 1)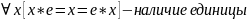 2)
2)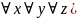
 .
Если в группе вып-ся коммутативность
.
Если в группе вып-ся коммутативность
 ,
то группа наз-ся абелевой. Пусть G-группа,
Н-наз-ся подгруппой группы G(H
,
то группа наз-ся абелевой. Пусть G-группа,
Н-наз-ся подгруппой группы G(H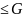 ),
если:
),
если:
1)a 2)
2) .
Если
H
.
Если
H .
Док-во: в силу 2) условия
.
Док-во: в силу 2) условия
 ,
в силу 1) условия a*
,
в силу 1) условия a* ,
a*
,
a* =e
=
=e
= ,
ассоциативность вып-ся из 1) условия
,
ассоциативность вып-ся из 1) условия
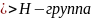 .
Примеры:1)
Gl(2,Q)={
.
Примеры:1)
Gl(2,Q)={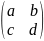 |a,b,c,d
|a,b,c,d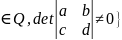 (Gl(2,Q),*,E,=) A*E=A=E*A, (A*B)*C=A*(B*C), detE=1
(Gl(2,Q),*,E,=) A*E=A=E*A, (A*B)*C=A*(B*C), detE=1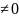 ,
A*
,
A* 2)
2) |A*B|=|A|*|B|=1*1=1 ? |
|A*B|=|A|*|B|=1*1=1 ? | |=1/|A|=1/1=1
3) , 4)(S(4),*,
|=1/|A|=1/1=1
3) , 4)(S(4),*, ,=).
4)
R
-
группа действительных чисел с операцией
сложения. (аддитивная группа действительных
чисел),5)C
- аддитивная
группа комплексных чисел. Подгруппа
<а
>
порожденная одним эл-ом а
наз-ся циклической. Она состоит из
всевозможных степеней порождающего
эл-та. <а >={
,=).
4)
R
-
группа действительных чисел с операцией
сложения. (аддитивная группа действительных
чисел),5)C
- аддитивная
группа комплексных чисел. Подгруппа
<а
>
порожденная одним эл-ом а
наз-ся циклической. Она состоит из
всевозможных степеней порождающего
эл-та. <а >={ }
}
2)
Смежные классы по подгруппе
С каждой подгруппы Н
группы G
можно связать множества:
gH=
{gh|h
H},
g
G,
которые наз-ся левыми смежными классами
группы G
по подгруппе Н. Hg=
{hg|h
H},
g
G,
которые наз-ся правыми смежными классами
группы G
по подгруппе Н. aH=bH
*b
H.
Док-во:
().
Пусть
 ,
,
 H.
a
= b
.
a
=
b
.
=
b
=>
b
H. ().
Пусть
b
H.
Тогда
b
=
(Найдутся такие
и
).
a
b
=a
=> b
=a
=> aH=bH.
Мощность множества левых и правых
смежных классов группы G
по подгруппе Н наз-ся индексом подгруппы
Н в группе G
и обозначаются
|
G:H|
Теорема
Лагранжа:
Если
H
≤G,
то |G|=|H|*|G:H|.
Число
элементов в группе равно числу элементов
подгруппы умноженное на индекс подгруппы
в группе.
Док-во:Поймем,что
левые смежные классы либо не пересекаются,
либо совпадают .
aH
H.
a
= b
.
a
=
b
.
=
b
=>
b
H. ().
Пусть
b
H.
Тогда
b
=
(Найдутся такие
и
).
a
b
=a
=> b
=a
=> aH=bH.
Мощность множества левых и правых
смежных классов группы G
по подгруппе Н наз-ся индексом подгруппы
Н в группе G
и обозначаются
|
G:H|
Теорема
Лагранжа:
Если
H
≤G,
то |G|=|H|*|G:H|.
Число
элементов в группе равно числу элементов
подгруппы умноженное на индекс подгруппы
в группе.
Док-во:Поймем,что
левые смежные классы либо не пересекаются,
либо совпадают .
aH
 bH
bH
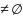 =>
=>
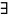 c
aH
bH.
c=a
, c=b
.
a
= b
.
a=
b
c
aH
bH.
c=a
, c=b
.
a
= b
.
a=
b
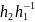 ,
H => a
bH => aH
,
H => a
bH => aH
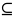 bH.
b=
b
bH.
b=
b
 ,
H => b
bH => bH
aH.
(aH
bH) & (bH
aH)
aH=bH.
Далее,
пусть
a
aH.
A=a*e
, e
H.
|H|=|aH|.
Строим
f:H
-> aH.
F(x)=ax,
где x
H.
Это
биекция.Док-во:
Пусть
,
H => b
bH => bH
aH.
(aH
bH) & (bH
aH)
aH=bH.
Далее,
пусть
a
aH.
A=a*e
, e
H.
|H|=|aH|.
Строим
f:H
-> aH.
F(x)=ax,
где x
H.
Это
биекция.Док-во:
Пусть
 тогда
тогда
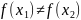 .Предположим,
что
.Предположим,
что
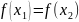 , тогда a
, тогда a , противоречие (Инъекция доказана).
Обратное
существует: Если f(x)=y=ax
то x=
y,
(сюръекция доказана).
Элементов
в Н столько же сколько в aH
, противоречие (Инъекция доказана).
Обратное
существует: Если f(x)=y=ax
то x=
y,
(сюръекция доказана).
Элементов
в Н столько же сколько в aH
H |
|
|
……………………………… |
|

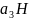
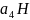
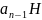
(чтд)
3)Классы сопряженности в группе. Централизаторы и нормализаторы. Элемент а сопряжен с элементом у в группе G, если найдется такой x из G,что x-1ax=y. a G aG={ay,y G}→мн-во сопр. эл. с эл-том
a={y-1ay|y G}. x≈y⟺xG=yG. ≈ – отношение экв-ти.
Теорема. Порядки сопряженных элементов равны.
Док-во: пусть x-1ax=b.Предположим что |a|=n, |b|=m, n˂m.Тогда (x-1ax)n=an=e, но bn≠e. Полученное противоречие док-т теорему. Сопряжение – отношен. экв-ти. Т.е. для сопр. выполняются 3 св-ва:
1)Рефлективность: x≈x xG=xG.
2)Симметрия: x≈y то y≈x. xG=yG⇒ yG=xG⇒ y≈x
3)Транзитивность: xG≈yG,yG=zG⇒xG=zG⇒x≈z.
1G=1G y-11y=1. zt=z⇒t-1zt=z⇒zt=tz. Из центра группы класс сопр. единичный.
Вообще, разл-е классы могут иметь разные мощ-и. Инстр-м измерения мощ-и класса служит нормализатор.
Теорема. Класс сопр-ти эл-та по мощности совпадает с индексом этого эл-та.
|aG|=G:C(a)|. a Z(G)⇒C(a)=G.
Док-во:
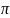 :aG
:aG
 {xC(a)|x
G}.
(ax)=xC(a).
{xC(a)|x
G}.
(ax)=xC(a).
Пусть
 ≠
≠ ⇒
⇒ ax1≠
ax1≠ a
a
Допустим x1(a)=x2C(a). x1C(a)= x2C()⇒ x2 C(a).
x1-1x2a=a x2⇒x2a=x1a x2
x2ax2-1=x1ax1-1 a( )=a( )
≠ |
x2-1x1C(a)=C(a). x2-1x1a=ax2-1x1.
Нормализатор подгруппы:
H≤G. N(H)={a G|a-1Ha=HG}. A-1Ha={aha|h=H}.
Лемма N(H) подгруппа G; H≤N(H)≤G
Док-во:N(H) подгруппа G: a,b N(H)⇒ ab N(H). h H. (ab)-1h(ab)=b-1a-1hab=
=b-1h 1b H⇒ab N(H). a N(H)⇒ a-1 N(H).
h H. (a-1)-1h(a-1)=aha-1=(a-1h-1a)-1 H⇒a-1 N(H). N(H) подгр. G. h H⇒h N(H).
h-1(n)h H⇒h N(H).
Централизатор подгруппы.
Пусть G группа.x G.
C(x)-центр-р. Предложение: Центр-р подмнож. яв-ся подгруппой в G.
Док-во:1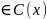 ,
C(x)≠0.
a,b
C(x).
,
C(x)≠0.
a,b
C(x).
Проверим, что ab C(x). Возьмем любой x X
(ab)x=abx=axb=x(ab)⇒ ab C(x).a ⇒a-1 C(x).
Пусть x X. ax=xa⇒ x=a-1xa⇒ xa-1=a-1x⇒ a-1 C(x).
C(x)={a G|ax=xa}
C(x)=
G=S(4). x=(1,2).
C(x)={a S(4)|ax=xa}
{,(1,2),(3,4),(1,2),(3,4)}
(1,2)(3,4)x=x(1,2)(3,4).
![]() 4
4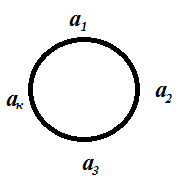 )Нормальные
подгруппы. Гомоморфизмы групп.
Нормальные
подгруппы.
Пусть
G=(s;∗)-группа,а
H=(T;∗),
T⊆S
,- ее
подгр.
Подгр. H
наз-тся
нормальной подгр.группы G,
если
для каждого эл-та aS
его
левые и правые смежные классы совпадают,
т.е.
если ∀aS
aH=Ha.
Сл-но,яв-ся
нормальной подгр.Заметим, что каждая
подгр. абелевой группы нормальна.
Если
подгр. Н нормальна в группе G,
то
левостороннее и правостороннее раложения
группы G
по
подгруппе совпадают.
Th.Подгр.
H=(T;∗)
яв-ся
нормальной подгр.группы G=(S;∗)
тогда
и только тогда, когда для каждого эл-та
S
для
любого элемента hH
верно,
что
a’∗h∗aH,
где
эл-т a’
симметричен
эл-ту a
в
группе G.Док-во.
⟹
Если
для каждого эл-та aS
верно
aH=Ha,
то для любого эл-та hH
найдется
такой эл-т
h1H,
что a∗h1=h∗a.
Откуда
a’∗(a∗h1)=a’∗(h∗a).Т.е.
а’∗h∗aH.
⟸.
Если
для каждого эл-та aS
для
любого эл-та hH
верно
a’∗h∗aH
, то a’∗h∗a=h1H.
Откуда
a∗(a’∗h∗a)=a∗h1
, h∗a=a∗h1
. Т.е.
Ha⊆aH.
Включение
aH⊆Ha
доказывается аналогично, рассамтривая
произведение (a’)’
∗h∗a’,
a’S.
Поэтому,
aH=Ha.
∎
Пример.
SL(n,k)⊲GL(n,k)
A∈SL(n,k)
detA=1
Det(B-1AB)=detB-1*detA*detB=detA=1
Пример.
G – абелева группа
H<G=>H⊲G
a-1ha=a-1ha=h∈H
Пример.
Докажем, что группа Н вращений правильного
треугольника в плоскости является
нормальной подгруппой группы S3.
S3={e=(1,2,3),(1)(23),(12)(3),(13)(2),(123),(132)},
И
подгруппа Н:
H={(1)(2)(3),(123),(132)}.Тогда
eH=h={(1)(2)(3),(123),!32)}=He,
И
(1)(23)H={(1)(23),(12)(3),(13)(2)}=H(1)(23).
Т.е.
подгруппа
Н – нормальная подгруппа группы S3.
Гомоморфизмы
групп.Пусть
)Нормальные
подгруппы. Гомоморфизмы групп.
Нормальные
подгруппы.
Пусть
G=(s;∗)-группа,а
H=(T;∗),
T⊆S
,- ее
подгр.
Подгр. H
наз-тся
нормальной подгр.группы G,
если
для каждого эл-та aS
его
левые и правые смежные классы совпадают,
т.е.
если ∀aS
aH=Ha.
Сл-но,яв-ся
нормальной подгр.Заметим, что каждая
подгр. абелевой группы нормальна.
Если
подгр. Н нормальна в группе G,
то
левостороннее и правостороннее раложения
группы G
по
подгруппе совпадают.
Th.Подгр.
H=(T;∗)
яв-ся
нормальной подгр.группы G=(S;∗)
тогда
и только тогда, когда для каждого эл-та
S
для
любого элемента hH
верно,
что
a’∗h∗aH,
где
эл-т a’
симметричен
эл-ту a
в
группе G.Док-во.
⟹
Если
для каждого эл-та aS
верно
aH=Ha,
то для любого эл-та hH
найдется
такой эл-т
h1H,
что a∗h1=h∗a.
Откуда
a’∗(a∗h1)=a’∗(h∗a).Т.е.
а’∗h∗aH.
⟸.
Если
для каждого эл-та aS
для
любого эл-та hH
верно
a’∗h∗aH
, то a’∗h∗a=h1H.
Откуда
a∗(a’∗h∗a)=a∗h1
, h∗a=a∗h1
. Т.е.
Ha⊆aH.
Включение
aH⊆Ha
доказывается аналогично, рассамтривая
произведение (a’)’
∗h∗a’,
a’S.
Поэтому,
aH=Ha.
∎
Пример.
SL(n,k)⊲GL(n,k)
A∈SL(n,k)
detA=1
Det(B-1AB)=detB-1*detA*detB=detA=1
Пример.
G – абелева группа
H<G=>H⊲G
a-1ha=a-1ha=h∈H
Пример.
Докажем, что группа Н вращений правильного
треугольника в плоскости является
нормальной подгруппой группы S3.
S3={e=(1,2,3),(1)(23),(12)(3),(13)(2),(123),(132)},
И
подгруппа Н:
H={(1)(2)(3),(123),(132)}.Тогда
eH=h={(1)(2)(3),(123),!32)}=He,
И
(1)(23)H={(1)(23),(12)(3),(13)(2)}=H(1)(23).
Т.е.
подгруппа
Н – нормальная подгруппа группы S3.
Гомоморфизмы
групп.Пусть
 Если
Если
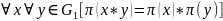 Пример:
Пример: .
Если
.
Если
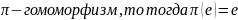 .
.
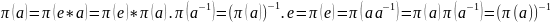 .
1)Если
.
1)Если
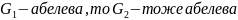 .
Если
.
Если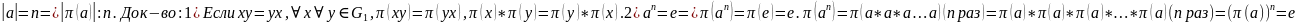
5)
Теорема о гомоморфизмах
Th.Если
:G1→G2
–гомоморфизм,
то: 1)Ker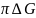 2)
Если Н
2)
Если Н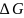 1,
то сущ-ет группа G2=
G1/H
и канонический гомоморфизм
1:
G1→G2
такой, что Ker
=Н
.
Док-во.
1)Пусть
x
1,
то сущ-ет группа G2=
G1/H
и канонический гомоморфизм
1:
G1→G2
такой, что Ker
=Н
.
Док-во.
1)Пусть
x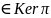 ,
y
,
y .
Xy=y-1xy.
.
Xy=y-1xy.
 2)Считаем
G2={aHǀa
G1}-
факторгруппа G1
по
Н . Зададим на G2
операцию хН*уН↔хуН . (хН*уН)*zH=xyH*zH=(xy)zH
. xH*(yH*zH)=xH*yzH=x(yz)H
. xH*x-1H=xx-1H=eH=H
. (xH)-1=x-1H
,e(1)=eH=H
. Строим
1(х)=xH.
(xy)=xyH=xH*yH=
(x)*
(y)
, сл-но
-
гомоморфизм . Ker
=
{x
G1ǀ
(x)=H}={x
G1ǀ
xH=H}={H}
2)Считаем
G2={aHǀa
G1}-
факторгруппа G1
по
Н . Зададим на G2
операцию хН*уН↔хуН . (хН*уН)*zH=xyH*zH=(xy)zH
. xH*(yH*zH)=xH*yzH=x(yz)H
. xH*x-1H=xx-1H=eH=H
. (xH)-1=x-1H
,e(1)=eH=H
. Строим
1(х)=xH.
(xy)=xyH=xH*yH=
(x)*
(y)
, сл-но
-
гомоморфизм . Ker
=
{x
G1ǀ
(x)=H}={x
G1ǀ
xH=H}={H}
