6 Синтез дискретной спр с регулятором скорости, обеспечивающим конечную длительность переходного процесса

Структурная схема дискретной системы управления представлена на рисунке 6.1.

Рисунок 6.1 – Упрощенная структурная схема системы подчиненного управления электроприводом с цифровым регулятором скорости

Определяем приведенную передаточную функцию непрерывной части с учетом экстраполятора:

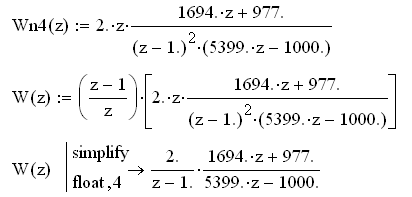
(6.1)

Выполняем факторизацию полиномов:

Q^*(z)= Q_-^*(z)Q₊^*(z); (6.2)

Q_-*(z)=(z – 1); n_q-=1; (6.3)

Q₊^*(z)=(z – 0,1852); n_q+=1; (6.4)

Определяем порядок желаемого полинома: G_ж(z)=z²_.

Определяем полиномы регулятора:

P^*(z)M₁^*(z)+ Q_-^*(z)N^*(z)=z². (6.5)

Порядок полинома M₁^*(z) n_M1=n_q- – 1 =0 и в общем виде полином имеет вид: M₁^*(z)=a₀.

Порядок полинома знамена теля совпадает с полиномом для регулятора: n_N = n_P = 1; N^*(z)=b₀+b₁z.

Подставим P^*(z), M₁^*(z), Q_-^*(z), N^*(z) в уравнение синтеза:

0,4536(z+0,5767)a₀+(z – 1)(b₀+b₁z)= z². (6.6)

Группируем:

b₁z²+b₀z – b₁z +0,4536a₀z – b₀ + 0,2616a₀=z²_. (6.7)

Приравняв коэффициенты в левой и правой части уравнения при одинаковых степенях z, получаем:

Искомые полиномы регулятора:

M₁^*(z)=a₀=1,398.

N^*(z)=b₀+b₁z= z + 0,366.

Определяем передаточную функцию регулятора:

(6.8)

7 АНАЛИЗ ДИСКРЕТНОЙ СПР С ПЕРЕХОДНЫМ ПРОЦЕССОМ КОНЕЧНОЙ ДЛИННЫ Переходной процесс может быть получен по следующей передаточной функции:

(6.9)

Реакция на ступенчатое воздействие:

(6.10)

Строим переходной процесс h^*(z) при реакции системы на единичное ступенчатое воздействие:

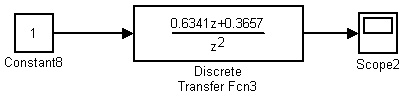
Рисунок 6.2 – Структурная схема исследуемой системы в среде MATLAB Simulink

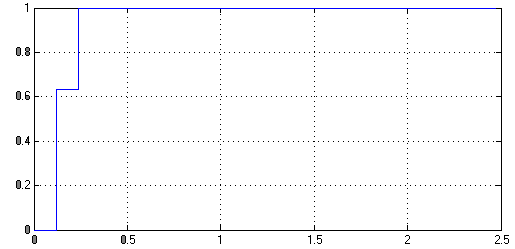
Рисунок 6.3 – Переходной процесс при реакции системы на единичное ступенчатое воздействие в среде MATLAB Simulink

8 Программная реализация регулятора, обеспечивающего конечную длительность переходного процесса дискретной спр

8.1 Листинг программы

Передаточную функцию регулятора представим в виде разностного уравнения:

Программа на языке Delphi:

unit Unit1;

interface

uses

Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms, Dialogs, StdCtrls, Buttons, TeEngine, Series, ExtCtrls, TeeProcs, Chart;

type

TForm1 = class(TForm)

Chart1: TChart;

BitBtn1: TBitBtn;

Series1: TLineSeries;

Edit1: TEdit;

Label1: TLabel;

Edit2: TEdit;

Label2: TLabel;

Edit3: TEdit;

Label3: TLabel;

Edit4: TEdit;

Label5: TLabel;

Edit7: TEdit;

Edit6: TEdit;

Label6: TLabel;

Edit8: TEdit;

Label7: TLabel;

Label8: TLabel;

Label4: TLabel;

Edit9: TEdit;

Label9: TLabel;

Label11: TLabel;

procedure BitBtn1Click(Sender: TObject);

procedure Edit1Exit(Sender: TObject);

procedure Edit6Exit(Sender: TObject);

procedure Edit2Exit(Sender: TObject);

procedure Edit7Exit(Sender: TObject);

procedure Edit3Exit(Sender: TObject);

procedure Edit8Exit(Sender: TObject);

procedure Edit4Exit(Sender: TObject);

procedure Edit9Exit(Sender: TObject);

private

{ Private declarations }

public

{ Public declarations }

end;

{Задаем массив}

type a=array[1..1000] of real;

var

Form1: TForm1;

implementation

{$R *.dfm}

procedure TForm1.BitBtn1Click(Sender: TObject);

var T,xinp,xout:real; n,i:integer;

x_inp,x_out:array[0..10000] of real;

ni_,no_:array[0..3] of real;

begin

ni_[0]:=StrToFloat(Edit1.Text);

ni_[1]:=StrToFloat(Edit2.Text);

ni_[2]:=StrToFloat(Edit3.Text);

ni_[3]:=StrToFloat(Edit4.Text);

no_[0]:=0;

no_[1]:=StrToFloat(Edit6.Text);

no_[2]:=StrToFloat(Edit7.Text);

no_[3]:=StrToFloat(Edit8.Text);

n:=StrToInt(Edit9.Text);

for i:=0 to n do

begin

x_inp[i]:=1;

xinp:=ni_[0]*x_inp[i]+ni_[1]*x_inp[i-1]+ni_[2]*x_inp[i-2]+

ni_[3]*x_inp[i-3];

xout:=no_[1]*x_out[i-1]+no_[2]*x_out[i-2]+no_[3]*x_out[i-3];

x_out[i]:=xinp+xout;

end;

Chart1.SeriesList.Series[0].Clear;

for i:=1 to n do

begin

Chart1.SeriesList.Series[0].AddXY(i-1,x_out[i]);

Chart1.SeriesList.Series[0].AddXY(i,x_out[i]);

end;

end;

procedure TForm1.Edit1Exit(Sender: TObject);

begin

if Edit1.Text<>'' then

try

StrToFloat(Edit1.Text);

except

on EConvertError do

begin

Edit1.SetFocus;

end;

end;

end;

procedure TForm1.Edit6Exit(Sender: TObject);

begin

if Edit6.Text<>'' then

try

StrToFloat(Edit6.Text);

except

on EConvertError do

begin

Edit6.SetFocus;

end;

end;

end;

procedure TForm1.Edit2Exit(Sender: TObject);

begin

if Edit2.Text<>'' then

try

StrToFloat(Edit2.Text);

except

on EConvertError do

begin

Edit2.SetFocus;

end;

end;

end;

procedure TForm1.Edit7Exit(Sender: TObject);

begin

if Edit7.Text<>'' then

try

StrToFloat(Edit7.Text);

except

on EConvertError do

begin

Edit7.SetFocus;

end;

end;

end;

procedure TForm1.Edit3Exit(Sender: TObject);

begin

if Edit3.Text<>'' then

try

StrToFloat(Edit3.Text);

except

on EConvertError do

begin

Edit3.SetFocus;

end;

end;

end;

procedure TForm1.Edit8Exit(Sender: TObject);

begin

if Edit8.Text<>'' then

try

StrToFloat(Edit8.Text);

except

on EConvertError do

begin

Edit8.SetFocus;

end;

end;

end;

procedure TForm1.Edit4Exit(Sender: TObject);

begin

if Edit4.Text<'' then

try

StrToFloat(Edit4.Text);

except

on EConvertError do

begin

Edit4.SetFocus;

end;

end;

end;

procedure TForm1.Edit9Exit(Sender: TObject);

begin

if Edit9.Text<>'' then

try

StrToFloat(Edit9.Text);

except

on EConvertError do

begin

Edit9.SetFocus;

end;

end;

end;

end.

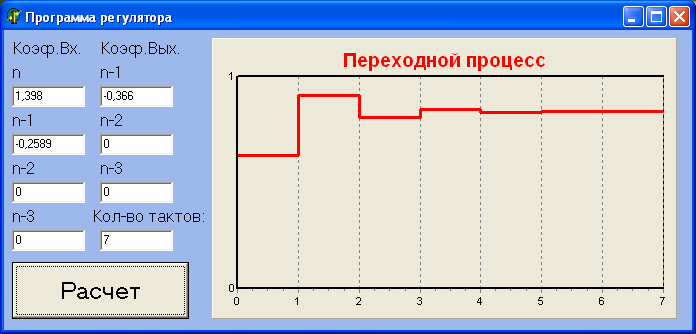
Рисунок 8.1 – Оболочка приложения