4 Определение периода квантования дискретной системы по критерию джури

Критерий Джури основывается на частотной характеристике непрерывной части системы, в качестве тестового сигнала для определения наибольшего допустимого периода квантования выбирается синусоидальное единичное воздействие.

. (4.1)

Произведем расчет в пакете Mathcad:

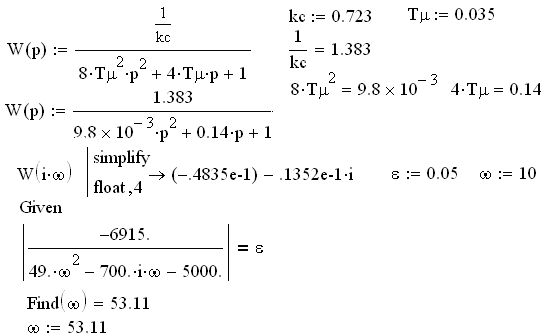
Рисунок 4.1 – Определение периода квантования дискретной системы по критерию Джури в пакете Mathcad

О

20

тсюда имеем: ω_к=53,11 с^-1.

Период квантования находим по формуле:

, (4.2) с.

5 Анализ дискретной системы с аналоговым регулятором момента и цифровым регулятором скорости

5.1 Определение передаточной функции дискретной СПР

Произведем z-преобразования передаточных функций элементов системы:

Экстраполятор:

. (5.1)

Непрерывная часть:

,где (5.2)

.

Произведём обратное преобразование Лапласа:

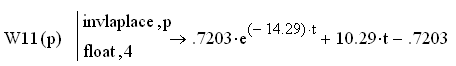
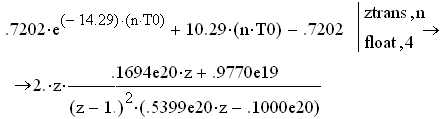
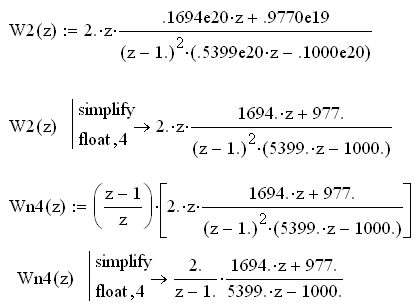
Определим передаточную функцию замкнутой системы в z-форме:

,

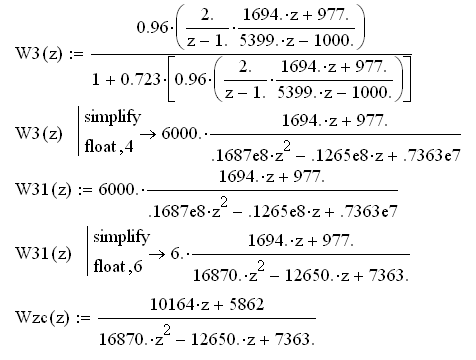
Передаточная функция замкнутой системы в z-форме:

.

5.2 Проверка устойчивости дискретной СПР по корням характеристического уравнения в плоскостях “z” и “w”

Проверим устойчивость дискретной СПР в среде Mathcad:

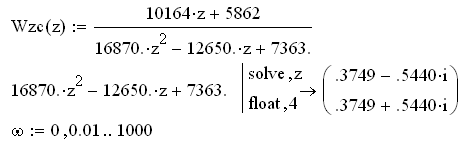
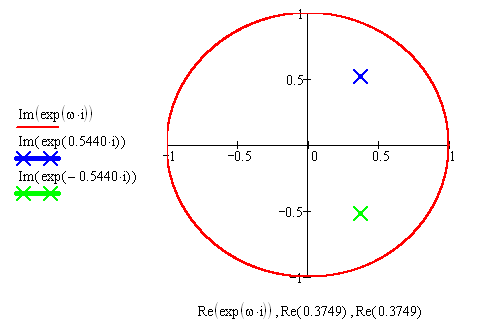
Рисунок 5.1 – Область устойчивости системы в плоскости «z»

Так как корни дискретной системы входят в область устойчивости в плоскости «z» (попадают в окружность единичного радиуса), то система устойчива.

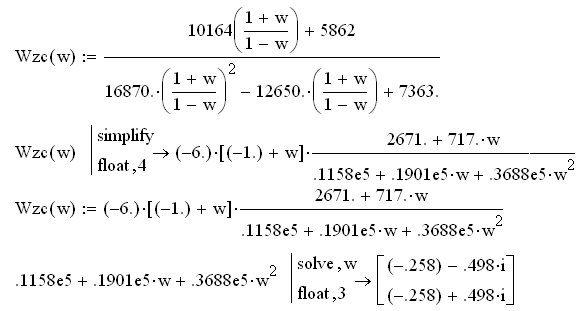
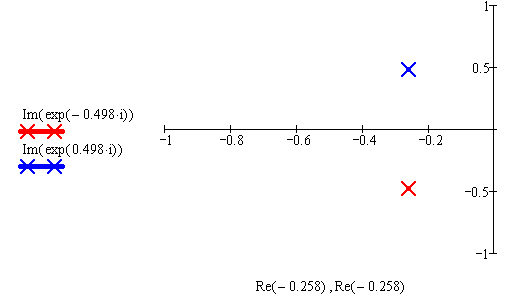
Рисунок 5.2 – Область устойчивости системы в плоскости «w»

Т.к. корни дискретной системы входят в область устойчивости в плоскости «w» (находятся в левой полуплоскости), то система устойчива.

5.3 Нахождение уравнения переходного процесса и показателей качества при реакции дискретной СПР на единичное ступенчатое воздействие

Если r(t) – единичное ступенчатое воздействие, то Z-преобразование для него:

(5.3)

Выходная координата:

(5.4)

(5.5)

Разделяем переменные:

(5.6)

Получаем разностное уравнение:

(5.7)

Перейдем от абсолютного времени к относительному:

(5.8)

Р

26

асчет параметров разностного уравнения с помощью таблиц Excel приведен в таблице 5.1.

Таблица 5.1 – Расчет параметров разностного уравнения

k	1.7498* *С[k-1]	-1.1863* *С[k-2]	0.43645* *С[k-3]	0.60248* *R[k-1]	0.34748* *R[k-2]	С[k]
0	0	0	0	0	0	0
1	0	0	0	0,60248	0	0,60248
2	1,05421	0	0	0	0,34748	1,40169
3	2,45269	-0,714722	0	0	0	1,73797
4	3,04110	-1,662836	0,262952	0	0	1,64121
5	2,87180	-2,061755	0,611771	0	0	1,42182
6	2,48790	-1,946978	0,758537	0	0	1,29946
7	2,27379	-1,686706	0,716310	0	0	1,30340
8	2,28069	-1,541552	0,620553	0	0	1,35969
9	2,37919	-1,546226	0,567150	0	0	1,40011
10	2,44992	-1,613007	0,568870	0	0	1,40579
11	2,45985	-1,660961	0,593439	0	0	1,39233
12	2,43630	-1,667690	0,611082	0	0	1,37969
13	2,41418	-1,651723	0,613557	0	0	1,37602
14	2,40776	-1,636731	0,607683	0	0	1,37871
15	2,41247	-1,632376	0,602167	0	0	1,38227
16	2,41869	-1,635572	0,600565	0	0	1,38369
17	2,42118	-1,639787	0,601741	0	0	1,38313
18	2,42020	-1,641472	0,603292	0	0	1,38202
19	2,41827	-1,640812	0,603911	0	0	1,38137
20	2,41712	-1,639501	0,603669	0	0	1,38129
21	2,41699	-1,638723	0,603186	0	0	1,38145
22	2,41726	-1,638631	0,602900	0	0	1,38153
23	2,41741	-1,638819	0,602866	0	0	1,38146
24	2,41728	-1,638918	0,602935	0	0	1,38130
25	2,41699	-1,638829	0,602972	0	0	1,38114
26	2,41672	-1,638636	0,602939	0	0	1,38102
27	2,41651	-1,638449	0,602868	0	0	1,38093
28	2,41636	-1,638311	0,602799	0	0	1,38085
29	2,41621	-1,638207	0,602748	0	0	1,38076
30	2,41605	-1,638108	0,602710	0	0	1,38065

График переходного процесса полученный с помощью пакета прикладных программ , приведен на рисунке 5.3.

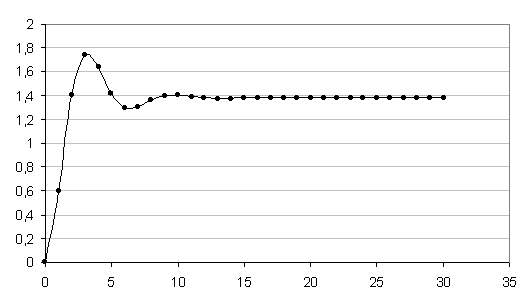
Рисунок 5.3 – График переходного процесса в дискретной САУ

Схема структурной модели цифровой САУ в пакете прикладных программ MATLAB Simulink приведена на рисунке 5.4.

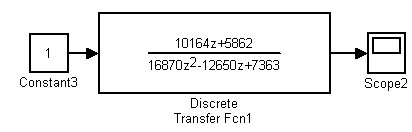
Рисунок 5.4 – Схемы структурной модели цифровой САУ

в пакете прикладных программ MATLAB Simulink

График переходного процесса в цифровой САУ, полученный с помощью пакета прикладных программ MATLAB Simulink, приведен на рисунке 5.5.

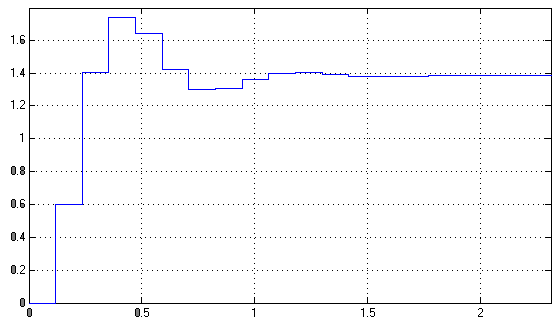
Рисунок 5.5 – График переходного процесса в цифровой САУ, полученный с помощью пакета прикладных программ MATLAB Simulink

Определим показатели качества из графика переходного процесса:

• перерегулирование:

;

• колебательность переходного процесса: ,6;

• длительность переходного процесса: с.