1 Синтез регуляторов скорости и момента при настройке контуров спр на модульный оптимум

Дана структурная схема системы подчиненного регулирования скорости ТПН-АД, состоящая из регулятора скорости, регулятора момента, тиристорного преобразователя напряжения, асинхронного двигателя и датчиков (рис.1.1).

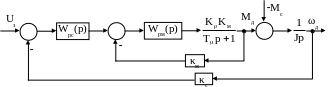
Рисунок 1.1 – Система подчиненного регулирования скорости ТПН-АД

На рисунке 1.1 приняты следующие обозначения:

κ_ρκ_м – коэффициент усиления тиристорного преобразователя напряжения;

Т_μ – постоянная времени тиристорного преобразователя;

J – момент инерции двигателя;

κ_м – коэффициент передачи датчика момента;

κ_с – коэффициент передачи датчика скорости.

Произведем синтез регуляторов скорости и момента при настройке контуров СПР на модульный оптимум.

Передаточная функция объекта контура момента в разомкнутом состоянии:

. (1.1)

Регулятор компенсирует ту часть объекта, которая не содержит Т_μ:

. (1.2)

Передаточная функция регулятора контура момента:

, (1.3)

.

Передаточная функция замкнутого контура момента:

(1.4) .

Передаточная функция объекта контура скорости:

. (1.5)

Регулятор компенсирует малую постоянную времени:

. (1.6)

Передаточная функция замкнутого контура скорости:

(1.7)

Передаточная функция регулятора скорости:

, (1.8)

.

2 Анализ непрерывной модели спр, настроенной на модульный оптимум

2.1 Определение передаточной функции СПР

Определим передаточную функцию контура момента:

(2.1)

Определим передаточную функцию замкнутой СПР:

. (2.2)

Характеристическое уравнение системы имеет вид:

. (2.3)

2.2 Проверка устойчивости СПР по корням характеристического уравнения в плоскости “р”

Произведем расчет корней характеристического уравнения (2.3) для настройки САУ на модульный оптимум в пакете прикладных программ Mathcad:

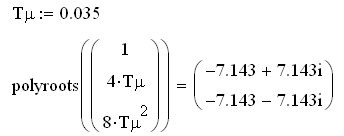
Р

16

исунок 2.1 – Расчет корней характеристического уравнения в среде пакета Mathcad

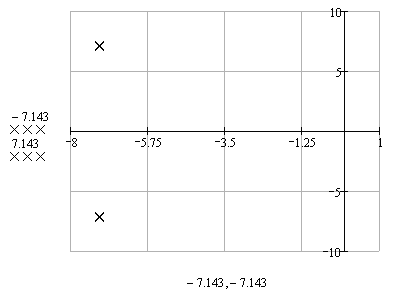
Рисунок 2.2 – Расположение корней характеристического уравнения

2.3 Нахождение уравнения переходного процесса и показателей качества при реакции СПР на единичное ступенчатое воздействие

Выполним построение переходного процесса с помощью пакета прикладных программ Mathcad:

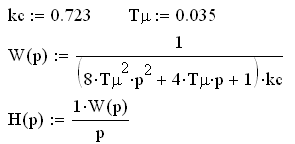
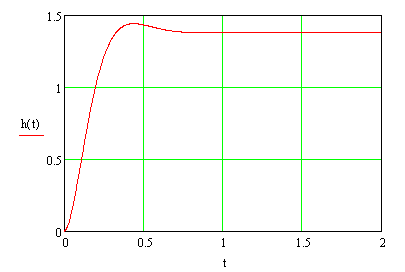
Рисунок 2.3 – Расчет и построение переходного процесса в среде пакета Mathcad при настройке САУ на модульный оптимум

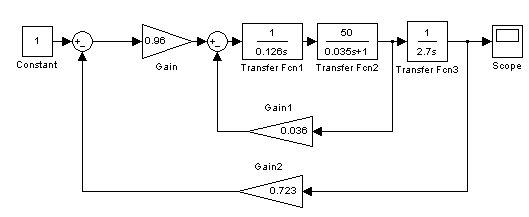
Рисунок 2.4 – Математическая модель аналоговой СПР в MatLab Simulink

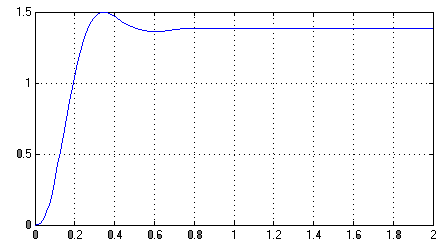
Рисунок 2.5 – График переходного процесса СПР при реакции на единичное ступенчатое воздействие в MatLab Simulink

Определим показатели качества из графика переходного процесса:

• перерегулирование:

;

• колебательность переходного процесса: ;

• длительность переходного процесса: 175 с.

3 Разработка структурной схемы дискретной спр

Для построения цифровой системы управления (ЦСУ) нам необходим вычислительный блок (регулятор скорости), квантователь (АЦП) и преобразователь кода в аналоговый сигнал (ЦАП). В состав аналоговой части входит объект управления.

Рисунок 3.1 – Упрощенная структурная схема системы подчиненного управления электроприводом с цифровым регулятором скорости

Передаточные функции элементов системы имеют следующий вид:

1. Передаточная функция дискретного регулятора скорости:

(3.1)

2. В качестве цифро-аналогового преобразователя будем использовать экстраполятор нулевого порядка с коэффициентом усиления, равным единице. Передаточная функция экстраполятор нулевого порядка в Z-форме:

. (3.2)

3. Передаточная функция непрерывной части:

(3.3)

4. Коэффициент обратной связи по скорости:

К_с=0,723. (3.4)