2.2. Пример решения задания № 2

Данные о доходе банка от операций с ценными бумагами за 2005–2009 гг. приведены в табл. 2.3.

Таблица 2.3 Доход банка от операций с ценными бумагами

за 2005–2009 гг.

Показатель	2005	2006	2007	2008	2009
Доход банка, млн руб.	92,0	105,0	129,0	157,0	175,0

Составить интервальный прогноз ожидаемого дохода банка от операций с ценными бумагами на 2011 год, гарантируя результат с заданной вероятностью 95 %.

Решение. Предполагаем, что доход банка от операций с ценными бумагами изменяется во времени по прямой . Для определения параметров и необходимо составить и решить систему нормальных уравнений (2.2):

Так как количество уровней в нашем ряду динамики нечетное, то отсчет времени (t) ведем от середины ряда (2007 год), согласно табл. 2.3.

В табл. 2.4 рассчитаны необходимые для решения системы суммы: , , .

Таблица 2.4. Расчетная таблица для определения

Параметров уравнения тренда

Год	Доход банка , млн руб.	t	t2
1	2	3	4	5	6	7	8
2005	92,0	–2	4	–184	88,0	4,0	16,0
2006	105,0	–1	1	–105	109,8	–4,8	23,04
2007	129,0	0	0	0	131,6	–2,6	6,76
2008	157,0	1	1	157	153,4	3,6	12,96
2009	175,0	2	4	350	175,2	–0,2	0,04
Итого	658,0	–	10	218	658,0	–	58,8

1. По итоговым данным (табл. 2.4) определяем параметры уравнения по формулам (2.5)

;

Получили уравнение основной тенденции дохода банка от операций с ценными бумагами за 2005–2009 годы:

(2.10)

Подставляя в полученное уравнение (2.10) соответствующие значения t, рассчитаем выровненные теоретические значения дохода банка от операций с ценными бумагами:

2005 год – млн руб.,

2006 год – млн руб.,

2007 год – млн руб.,

2008 год – млн руб.,

2009 год – млн руб.

Полученные значения записываем в графу 6 табл. 2.4 и подсчитываем сумму. При этом сумма выровненных значений должна равняться сумме исходных данных ряда динамики (658,0), если это не так, то параметры уравнения тренда определены неверно.

2. Для оценки точности замены ряда динамики уравнением тренда определим оценку погрешности по формуле (2.6).

В нашем примере доход банка от операций с ценными бумагами предоставлен за 5 лет, поэтому n = 5. Уравнение тренда мы выбрали в виде уравнения прямой линии, следовательно, m = 2.

Среднее значение уровня ряда равно параметру .

Вычисляем квадрат разности между исходными уровнями динамического ряда и выровненными значениями – . Полученные значения записываем в графу 8 табл. 2.4 и подсчитываем сумму – .

3. На основе полученного уравнения тренда можно строить прогнозные значения дохода банка от операций с ценными бумагами для разных периодов времени путем подстановки в уравнение значений временной компоненты. Для 2010 года величина t = 3, а для 2011 года t = 4 и т. д.

Следовательно, для 2011 года мы получим следующую ожидаемую величину дохода банка от операций с ценными бумагами:

млн руб.

4. Для составления интервального прогноза ожидаемого дохода банка от операций с ценными бумагами по формуле (2.8) определим среднее квадратическое отклонение от тренда, скорректированное по числу степеней свободы:

млн руб.

Для заданной вероятности Ф(t) = 95 % определяем уровень значимости .

Для числа степеней  = 5 – 2 = 3 и при уровне значимости определяем по табл. 2.5 коэффициент доверия .

Таблица 2.5. Значения коэффициента доверия

по распределению Стьюдента

Число степеней свободы 	Уровень значимости 
	0,05	0,01
1	12,706	63,657
2	4,303	9,925
3	3,182	5,841
4	2,776	4,604
5	2,571	4,032
6	2,447	3,707
7	2,365	3,499
8	2,306	3,355

Вероятностные границы интервала прогнозируемого дохода банка от операций с ценными бумагами вычисляем по формуле (2.9)

.

Подставив все значения, получим

Следовательно, с вероятностью, равной 95 %, можно утверждать, что доход банка от операций с ценными бумагами в 2011 году не менее чем 204,71 млн руб., но не более чем 232,89 млн руб.

5. Строим график динамики дохода банка от операций с ценными бумагами за период с 2005 по 2009 гг. (рис. 2.1).

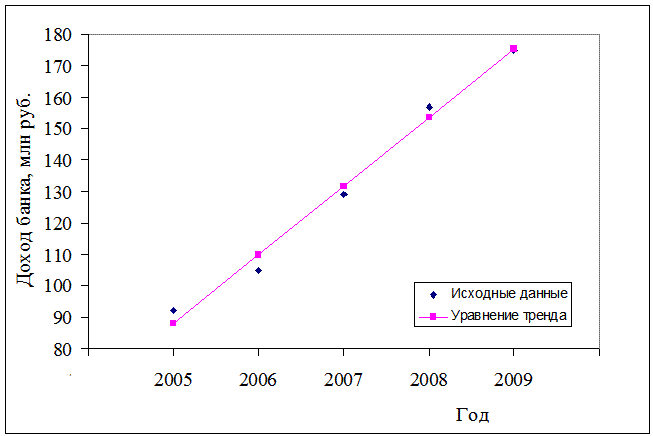
Рис. 2.1. Динамика доходов банка от операций с ценными бумагами

за 2005–2009 годы

3. ЗАДАНИЕ № 3

С помощью коэффициента ассоциации, коэффициента контингенции, коэффициентов взаимной сопряженности Пирсона и Чупрова, коэффициентов корреляции рангов Спирмэна и Кендэла необходимо исследовать взаимосвязь между явлениями и оценить тесноту этой связи.

3.1. Краткая теория

3.1.1. Статистические методы изучения взаимосвязей

социально-экономических явлений

При исследовании социально-экономических явлений часто приходится иметь дело с взаимосвязанными показателями.

Связи между социально-экономическими явлениями – это причинно-следственные отношения. Различают факторные и результативные признаки.

Признаки, характеризующие следствие, называются результативными, признаки, характеризующие причину, – факторными.

Особое место в изучении взаимосвязи занимает исследование особенностей распределения единиц совокупности по двум признакам в таблицах взаимосопряженности размерностью . По характеру распределения можно судить, случайно оно или нет, т. е. есть ли зависимость между признаками, положенными в основу группировки, или нет.

Простейшая форма таблицы взаимной сопряженности – таблица «четырех полей», которая имеет следующий вид:

a	b	a + b
c	d	c + d
a + c	b + d	a + b + c + d

В ней по каждому признаку выделяются только две группы, чаще всего по альтернативному признаку («да – нет», «хорошо – плохо»).

Для измерения тесноты связи между группировочными признаками в таблицах взаимной сопряженности могут быть использованы такие показатели, как коэффициент ассоциации, коэффициент контингенции, коэффициенты взаимной сопряженности Пирсона и Чупрова.

Коэффициент ассоциации, коэффициент контингенции могут применяться лишь для исследования взаимосвязи между двумя качественными альтернативными признаками.

Коэффициент ассоциации выражается следующей формулой (применительно к таблице «четырех полей», частоты которых обозначены через a, b, c, d):

. (3.1)

Коэффициент контингенции:

. (3.2)

Оба коэффициента изменяются от –1 до +1. Коэффициент контингенции всегда оказывается меньше коэффициента ассоциации, он дает более «осторожную» оценку взаимосвязи признаков. Связь считается существенной, если > 0,5 и > 0,3.

Коэффициенты взаимной сопряженности Пирсона и Чупрова применяются для определения взаимосвязи двух качественных признаков, если они состоят более чем их двух групп, т. е. не являются альтернативными.

Коэффициент взаимной сопряженности Пирсона определяется по формуле

, (3.3)

где – показатель взаимной сопряженности; рассчитывается как

, (3.4)

здесь k – число групп признака х ; m – число групп признака y ; – количество единиц, одновременно относящихся к i-й группе признака х и к j-й группе признака y; – количество единиц -й группы; – количество единиц -й группы

Коэффициент взаимной сопряженности Чупрова рассчитывается по формуле

= . (3.5)

Коэффициенты взаимной сопряженности Пирсона и Чупрова изменяются от 0 до 1, но уже при значении 0,3 можно говорить о тесной связи между вариацией изучаемых признаков.