1.1.3. Структурные средние величины

Структурные средние – мода и медиана – характеризуют величину варианта, занимающего определенное положение в ранжированном ряду.

Мода – наиболее часто встречающееся значение признака в данном ряду распределения, т. е. имеющее наибольшую численность в ряду распределения.

В дискретном ряду мода определяется визуально, т.е. отыскивается просмотром численностей, которые имеют варианты признака. Значение признака, имеющее наибольшую численность (в абсолютном или относительном выражении), и есть мода. Если несколько значений признака имеют одинаковую, наибольшую по сравнению с другими численность, то, следовательно, в ряду не одна, а несколько мод, например две. Ряд с двумя модами называется двумодальным.

Мода для интервального ряда распределения с равными интервалами определяется по формуле

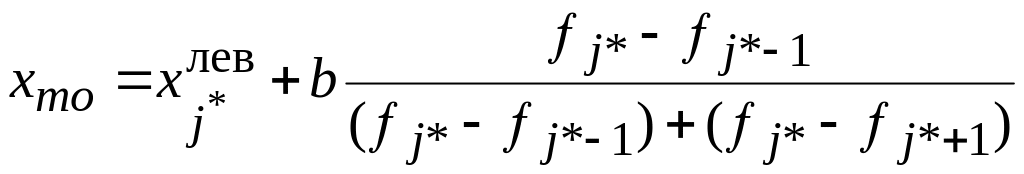, (1.5)

где – левая граница модального интервала; b – величина модального интервала; – частота модального интервала; – частота интервала, предшествующего модальному; – частота интервала, следующего за модальным.

Медиана – это значение признака, приходящееся на середину ранжированного ряда, т. е. это вариант, который делит ряд распределения на две равные по объему части. При нормальном распределении статистической величины мода и медиана совпадают со средним значением этой величины: .

Для определения медианы сначала определяют ее место в ранжированном ряду, используя формулу

, (1.6)

где п – число членов ряда.

Если совокупность содержит четное число значений варьирующего признака (п = 2 k, k = n/2), то в этом случае за медиану условно принимают значение

,

так как в ряду нет члена, который делил бы совокупность на две равные по объему группы.

В дискретном ряду распределения медиана определяется непосредственно по накопленной частоте, соответствующей номеру медианы.

В интервальном ряду распределения сначала указывают интервал, в котором находится медиана.

Медианным является первый интервал, в котором сумма накопленных частот превысит половину общего числа наблюдений.

Медиана для интервального ряда распределения с равными интервалами определяется по формуле

, (1.7)

где – нижняя граница медианного интервала; – накопленная частота интервала, предшествующего медианному, – частота медианного интервала.

1.1.4. Показатели вариации

Вариация – изменения значения признака в пределах совокупности.

Показатели вариации делятся на две группы: абсолютные и относительные.

К абсолютным показателям вариации относятся: размах колебаний, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение.

1. Размах колебаний, или размах вариации, представляет собой разность между максимальным и минимальным значениями признака в изучаемой совокупности.

Размах вариации определяется по формуле

. (1.8)

Безусловным достоинством этого показателя является простота расчета. Однако размах вариации зависит от величины только крайних значений признака, поэтому область его применения ограничена достаточно однородными совокупностями. В частности, на практике он находит применение в предупредительном контроле качества продукции.

2. Среднее линейное отклонение d и среднее квадратическое отклонение  показывают, на сколько в среднем отличаются индивидуальные значения признака от среднего его значения.

Среднее линейное отклонение определяется по формуле

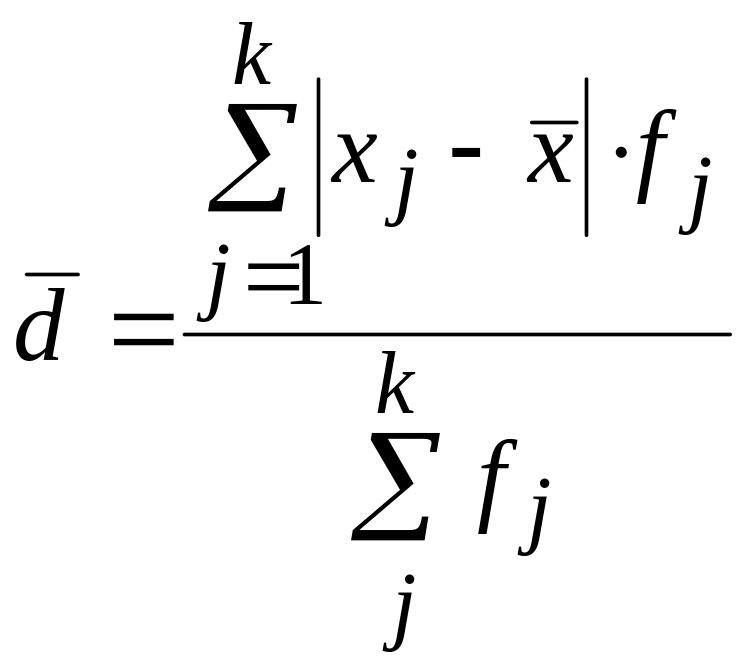. (1.9)

Среднее линейное отклонение имеет ту же размерность, что и признак, для которого оно вычисляется.

3. Дисперсия представляет собой средний квадрат отклонений вариантов признака от средней величины и определяется по формуле

. (1.10)

Дисперсию можно определить и как разность между средним квадратом вариантов признака и квадратом их средней величины, т. е.

где

4. Среднее квадратическое отклонение  – корень второй степени из дисперсии и определяется по формуле

. (1.11)

Для характеристики степени однородности совокупности, типичности, устойчивости средней, а также и для других статистических оценок используются относительные показатели вариации. Они вычисляются как отношение абсолютных показателей вариации к средней арифметической (или медиане) и чаще всего выражаются в процентах.

Формулы расчета относительных показателей вариации следующие:

коэффициент осцилляции 100 %, (1.12)

относительное линейное отклонение 100 %, (1.13)

коэффициент вариации 100 %. (1.14)

Наиболее часто применяется коэффициент вариации. Его используют не только для сравнительной оценки вариации, но и для характеристики однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33 % (для распределений, близких к нормальному).