Раздел 4

4-1.1 Двумерная плотность вероятности случайного процесса равна вероятности того, что:

Ответ: Все приведенные выше ответы ошибочны

4-1.2 Двумерная функция распределения вероятности случайного процесса равна вероятности того, что:

Ответ: Все приведенные выше ответы являются ошибочны

4-1.3 Совместная плотность вероятностей (2+2)-порядка двух случайных процессов и равна вероятности того, что:

Ответ: Все приведенные выше ответы являются ошибочными

4-2.1 Случайный процесс является стационарным, если:

Ответ: Все приведенные выше ответы являются ошибочными

4.2-2 Если случайный процесс является стационарным в широком смысле, то:

Ответ:

4-2.3 Если случайный процесс является эргодическим, то:

Ответы: для любых выполняется равенство

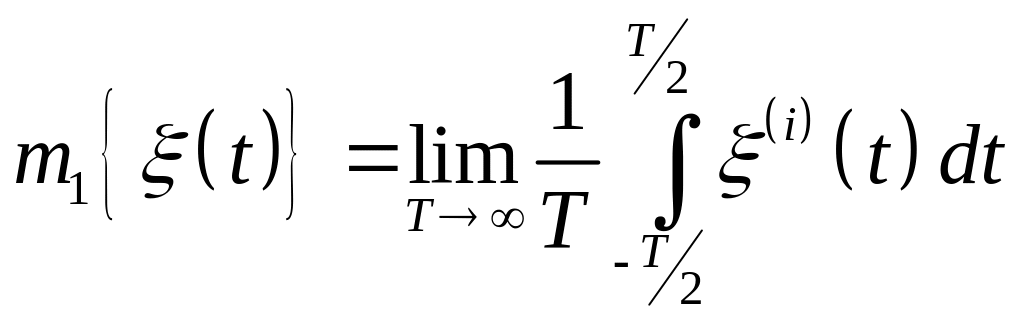для любой i-ой реализации

4-3.1 процесс , где А – случайная величина, не зависящая от времени, является

Ответ:все приведенные ответы ошибочны

4-3.2 процесс , где фи – не зависящая от времени случайна величина, является

Ответ: стационарным и эргодическим, если фи распределена равномерно в пределах [0, 2*pi]

4-3.3 процесс , где А и фи не зависящие от времени случайные величины, является

Ответ: все приведенные выше ответы являются ошибочными

4-4.1 корреляционная функция стационарного случайного процесса обладает свойствами

Ответ: все приведенные ответы ошибочны (ответ - )

4-4.2 коэффициент корреляции стационарного случайного процесса равен

Ответ:

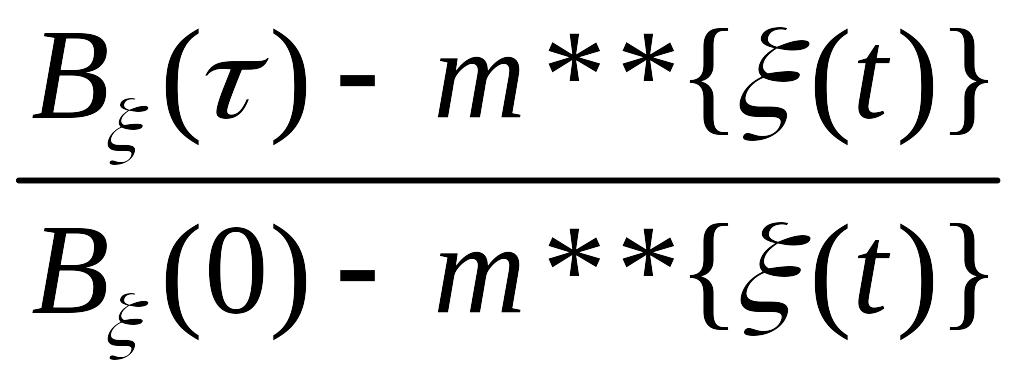
4-4.3 корреляционная функция отклонения случайного процесса равна

Ответ:

4-4.4 случайные процессы и являются стационарно связанными, если

Ответ:

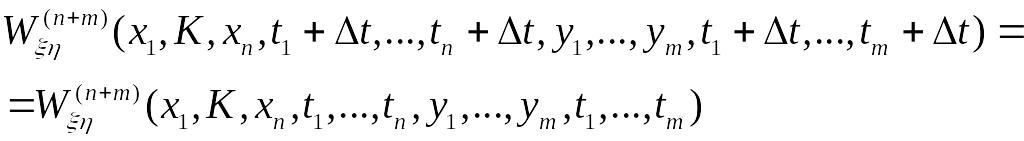
4.5.1. энергетический спектр стационарного случайного процесса представляет собой

Ответ: спектральную плотность средней мощности процесса

4.5.2 энергетический спектр стационарного случайного процесса связан с корреляционной функцией этого процесса соотношением

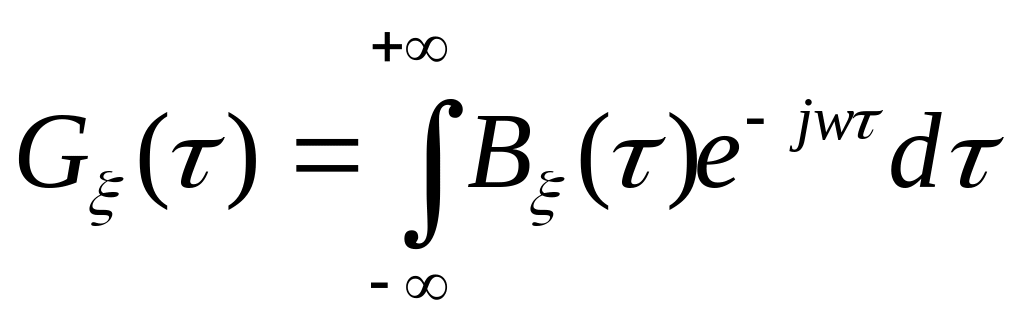
Ответы:

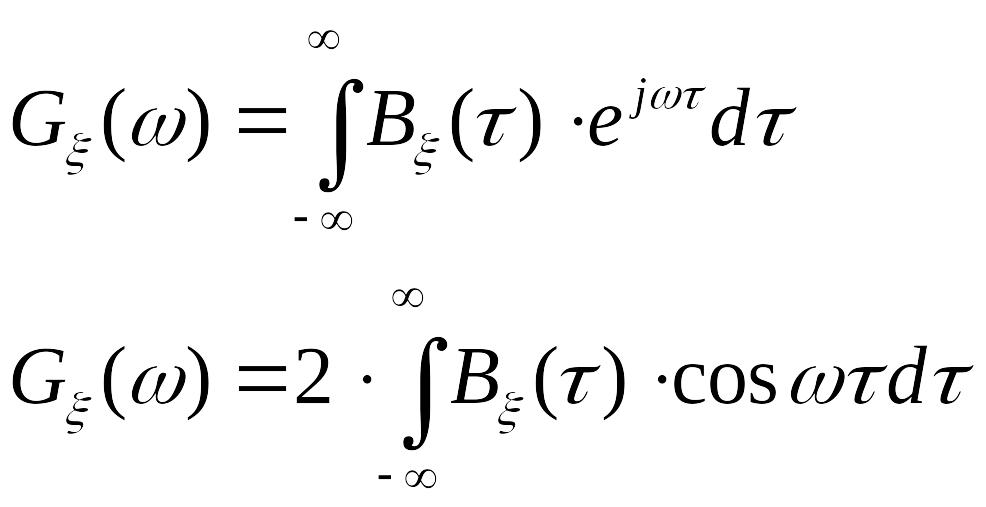
4.5.3 энергетический спектр стационарного случайного процесса может быть представлен в форме

Ответы: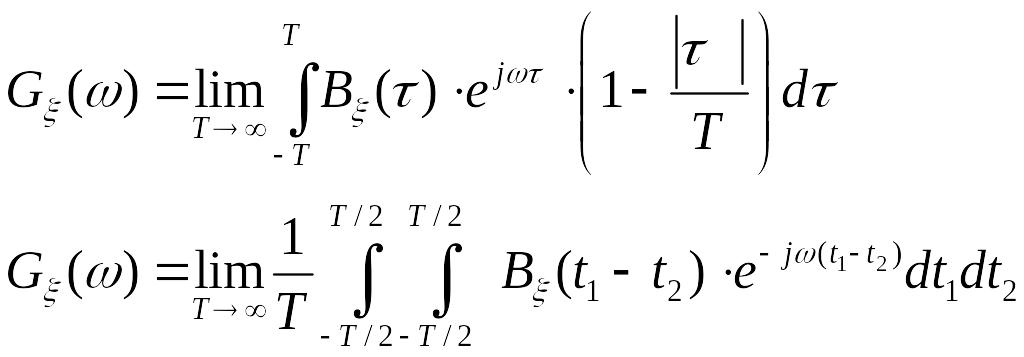

4-6.1-2 средняя мощность стационарного случайного процесса равна

Ответы: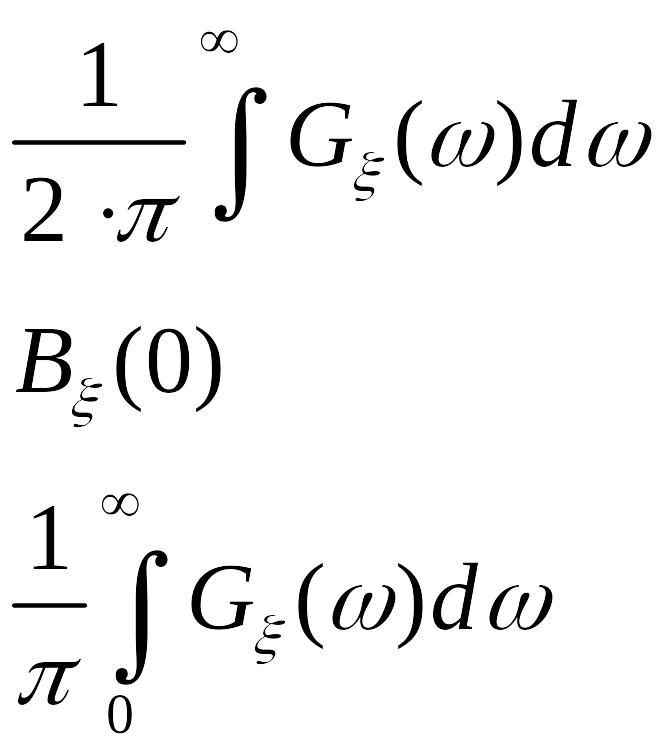

4-6.3 средняя мощность стационарного случайного процесса равна

Ответ: все приведенные ответы ошибочны

4-7.1. ширина полосы частот, занимаемой широкополосным случайным процессом , энергетический спектр которого включает нулевую частоту, может быть представлена в форме решения уравнения

Ответ: все приведенные ответы ошибочны

4-7.2. ширина полосы частот, занимаемой относительно узкополосным процессом с энергетическим спектром (с центральной частотой ), может быть представлена в форме решения уравнения

Ответы: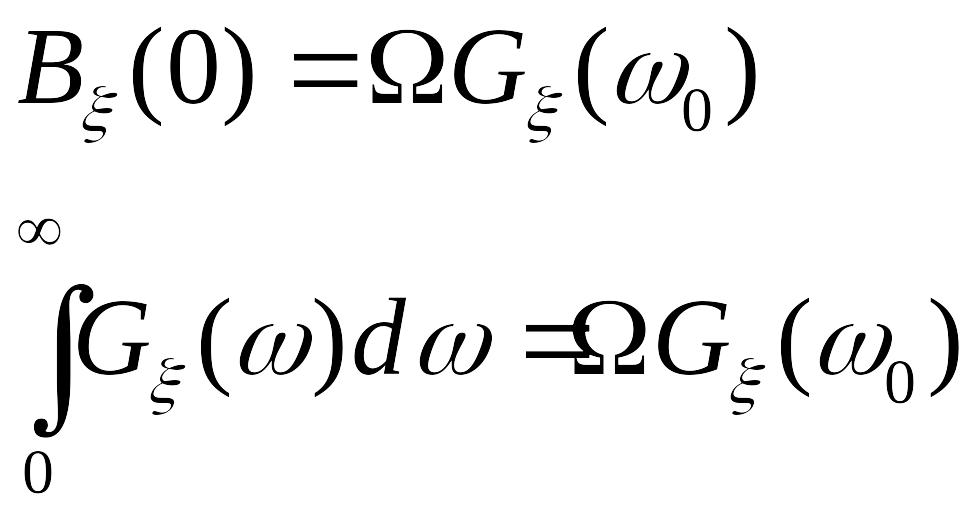

4-7.3 ширина интервала корреляции стационарного процесса может быть представлена в форме

Ответ: все приведенные ответы ошибочны

4-7.4 ширина интервала корреляции стационарного случайного процесса может быть представлена в форме

Ответ: все приведенные ответы ошибочны

4-8.1 Энергетический спектр стационарного случайного процесса отличен от нуля в

области и равен Тогда функция автокорреляции этого процесса равна:

Ответ:

4-8.2 Энергетический спектр стационарного случайного процесса отличен от нуля в

области и равен Тогда функция автокорреляции этого процесса равна:

Ответ:

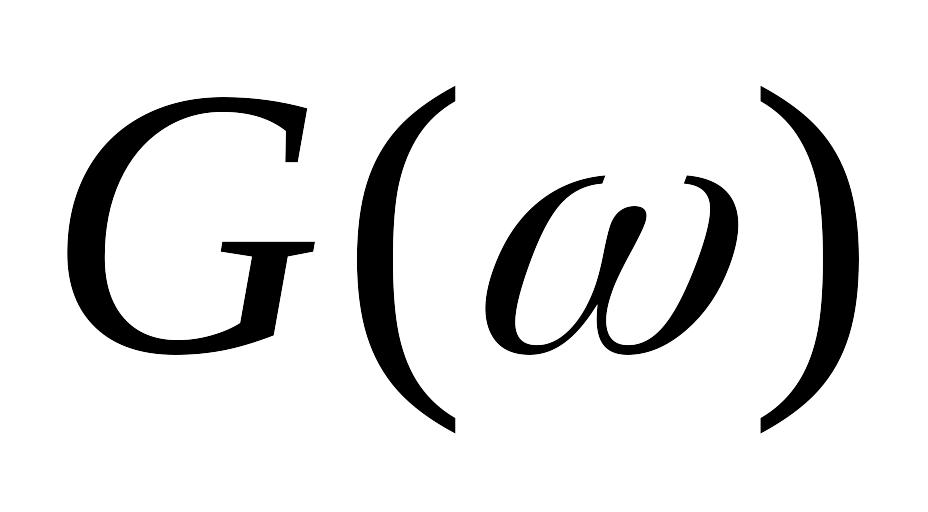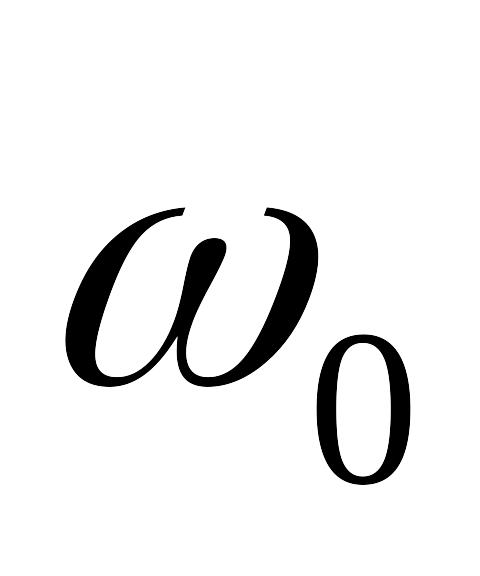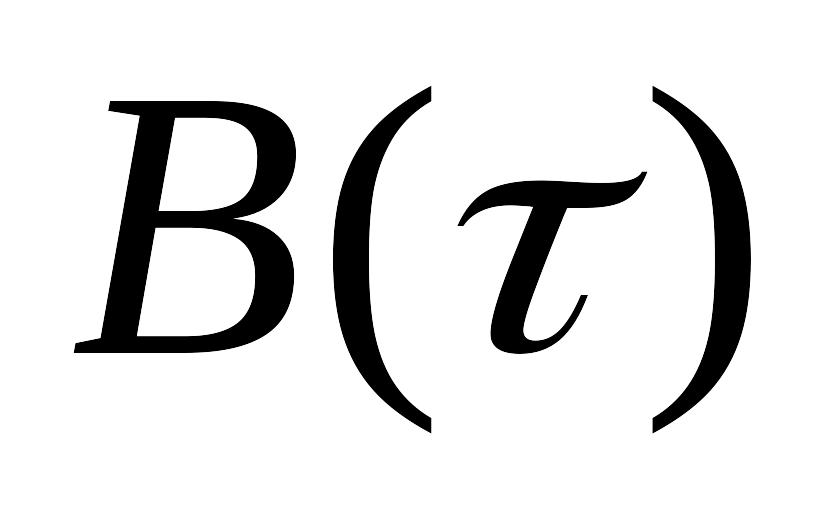3. Энергетический спектр узкополосного стационарного случайного процесса симметричен относительно частоты в области . Тогда функция автокорреляции этого процесса связана с функцией автокорреляции эквивалентного низкочастотного процесса соотношением:

Ответ:

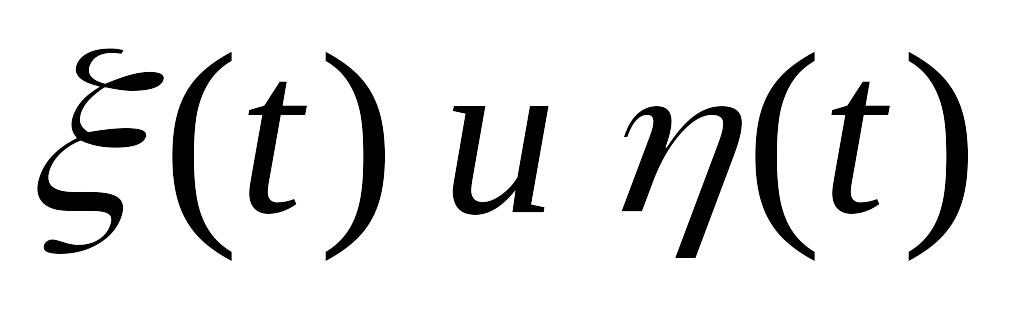1. Взаимная корреляционная функция стационарных и стационарно связанных случайных процессов обладает свойством:

Ответ:

2. Взаимный энергетический спектр стационарных и стационарно связанных

случайных процессов связан с взаимной корреляционной функцией этих процессов соотношением: Ответ:

3. Взаимный энергетический спектр стационарных и стационарно связанных случайных процессов обладает свойством:

Ответ:

4-10.1 Низкочастотные квадратурные компоненты узкополосного гауссовского

случайного процесса представляют собой случайные процессы с одномерным распределением:

Ответ:Гаусса

2. Огибающая узкополосного гауссовского случайного процесса имеет одномерное

распределение:

Ответ:Релея-Райса

2. Фаза узкополосного гауссовского случайного процесса, представляющего смесь полезного сигнала и шума, имеет одномерное распределение:

Ответ:Все приведенные ответы ошибочны

2. Для определения многомерной плотности вероятности марковского случайного

процесса любого порядка достаточно задать:

Ответ:Двумерную плотность вероятности

4-10.5 Каноническое разложение случайного процесса предполагает представление

процесса в виде ряда, коэффициенты которого:

Ответы:Статически независимы

Некоррелированы