Раздел 1

1. Интегральная и дифференциальная функции распределения случайной величины ξ равны соответственно и . При этом вероятность :

Ответ: Все приведённые ответы ошибочны

2. Дискретная часть плотности вероятности смешанной случайной величины ξ равна: 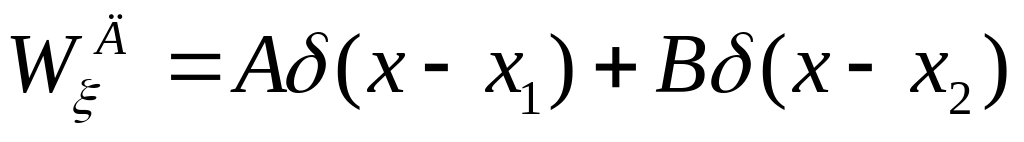. Тогда вероятность равна:

Ответ: Все приведённые ответы не правильны

3. Плотность вероятности смешанной случайной величины ξ равна: , где -непрерывная часть плотности и .

Вероятность того, что значение величины ξ не превосходит , равны:

Ответ:

1. Характеристики безынерционного преобразователя имеет вид:

На входе преобразователя имеется непрерывный случайный процесс ξ(t). Тогда плотность вероятности процесса η(t) на выходе такого преобразователя равна:

Ответ:

2. Характеристики безынерционного преобразователя имеет вид:

На входе преобразователя имеется непрерывный случайный процесс ξ(t). Тогда одномерная

плотность вероятности процесса η(t) на выходе такого преобразователя равна:

Ответ:Все приведённые ответы не правильны

1. Случайные величины и имеют ковариацию . Отсюда следует, что их совместная

плотность вероятностей удовлетворяет условию:

Ответ:Все приведённые ответы не правильны

2. Случайные величины и имеют ковариацию . Отсюда следует, что их совместная

плотность вероятностей удовлетворяет условию:

Ответ:Все приведённые ответы не правильны

3. Случайные величины и имеют ковариацию . Отсюда следует, что их совместная

плотность вероятностей удовлетворяет условию:

Ответ:Все приведённые ответы не правильны

4. Случайные величины и статистически независимы. Отсюда следует, что их ковариация удовлетворяет условию:

Ответ:

5. Совместное распределение случайных величин и имеют вид:

Их ковариация равна:

Ответ:r

6. Совместное распределение случайных величин и имеют вид:

Их коэффициент корреляции равен:

Ответ: r

1-4 Случайная последовательность импульсов единичной амплитуды положительной и отрицательной

полярности, поступающих на суммирующее устройство, описывается биноминальным распределением

вероятностей, причём р – вероятность появления положительного импульса. Вероятность того, что

сумма n последовательно поступивших импульсов окажется равной величине m , описывается

выражением:

Ответ:

1. Распределение Пуассона описывает:

Ответ:Вероятность того, что некоторое редкое событие произойдёт ровно k-раз на заданном инт. вр

2. Распределение Пуассона справедливо для потока редких событий, удовлетворяющего условию ординарности. Это означает, что:

Ответ:Все приведённые ответы не правильны

3. Распределение Пуассона справедливо для потока редких событий, удовлетворяющего условию стационарности. Это означает, что:

Ответ: Все приведённые ответы не правильны

4. Распределение Пуассона справедливо для потока редких событий, удовлетворяющего условию отсутствия последействия. Это означает, что:

Ответ:Все приведённые ответы не правильны

1. Статистика интервалов времени τ между соседними событиями описывается функцией распределений .При этом величина λ имеет смысл:

Ответ:среднего числа событий в единицу времени

2. Статистика интервалов времени τ между соседними событиями описывается функцией распределений .При этом вероятность того, что за время τ не произойдёт ни одного события,равна:

Ответ:Все приведённые ответы не правильны

3. Статистика интервалов времени τ между соседними событиями описывается функцией распределений . Тогда вероятность того, что за время Т не произошло ни одного события, равна:

Ответ:

1. Плотность вероятности значений случайной величины ξ описывается законом Рэлея. Это значит, что:

Ответ:Все приведённые ответы не правильны

2. Плотность вероятности значений случайной величины ξ описывается законом Рэлея. Дисперсия ξ равна . Это значит,что :

Ответ:

3. Плотность вероятности значений случайной величины ξ описывается законом Рэлея с дисперсией . Тогда вероятностьтого, что значение ξ превосходит некую величину , равна:

Ответ:

4. Значения случайной величины ξ равновероятны в пределах . Тогда интегральная функция распределения в пределах имеет вид:

Ответ:

5. Шум квантования описывается равномерно распределённой (в пределах ) случайной величиной. Вероятность того, что ошибка квантования примет положительное значение, равна:

Ответ:Все приведённые ответы не правильны

1. Условная функция распределения случайной величины η, зависящей от случайной величины ξ, может быть представлена в виде:

Ответ:Все приведённые ответы не правильны

2. Безусловная функция распределения случайной величины η, зависящей от случайной величины ξ, может быть представлена в виде:

Ответ:Все приведённые ответы не правильны

3. Условная плотность вероятности случайной величины η, зависящей от случайной величины ξ, может быть представлена в виде:

Ответ:

4. Совместная плотность вероятностей двух случайных величин ξ и η может быть представлена в виде:

Ответы:

5. Какие из приведённых ниже соотношений являются ошибочными ?

Ответы:

6. Какие из приведённых ниже соотношений являются ошибочными ?

Ответ:Все приведённые ответы верны

7. Условное математическое ожидание величины η , зависящей от ξ, может быть представлено:

Ответ:

8. Условная дисперсия величины η , зависящей от ξ, может быть представлена в виде:

Ответ:Все приведённые ответы не правильны

1. Случайная величина ξ равна сумме двух независимых случайных величин η и ν. В качестве оценки у значения случайной величины η по результату x измерения случайной величины ξ выбирается значение y, соответствующее максимуму апостериорного распределения величины η. Это означает,

что y соответствует максимуму функции:

Ответ:

2. Случайная величина η равна сумме двух независимых случайных величин ξ и ν. Величина ξ имеет равномерное распределение в интервале . Величина ν имеет центрированное нормированное нормальное распределение. В качестве оценки х значения случайной величины ξ по результату у измерения величины η выбирается оценка по максимуму апостериорного распределения величины. Тогда:

Ответ:Все приведённые ответы ошибочны

1-9.3 Случайная величина равна сумме двух независимых случайных величин Величина имеет распределение вида: . Величина имеет центрированное нормальное распределение с дисперсией . В качестве оценки x значений случайной величины по результату y измерения величины выбирается оценка по максимуму апостериорного распределения . Тогда:

Ответ:

Ответ не дан