31.Уравнение состояния идеального газа. Изопроцессы. Адиабатический процесс. Политропический процесс.

Идеальный газ можно рассматривать как совокупность беспорядочно движущихся молекул-шариков, имеющих пренебрежимо малый собственный объем и не взаимодействующих друг с другом на расстоянии.

Законы, описывающие поведение идеальных газов.

1. Процесс, происходящий при постоянной температуре, называется изотермическим:

Для данной массы газа m при постоянной температуре T произведение давления p на объем V есть величина постоянная: pV=const при T=const и m=const.

Кривая, изображающая зависимость между p и V , характеризующая свойства вещества при постоянной температуре, называется изотермой. Изотермы — гиперболы, расположенные на графике тем выше, чем выше температура происходящего процесса

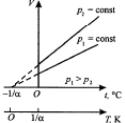
2. Процесс, происходящий при постоянном давлении, называется изобарным:

Для данной массы газа m при постоянном давлении p отношение объема V к температуре T есть величина постоянная.

V/T=const при p=const и m=const.

Кривая (Рис.2, нижний график), изображающая зависимость между V и T, характеризующая свойства вещества при постоянном давлении, называется изобарой. Если использовать температуру по шкале Цельсия, то закон можно записать в следующей форме V=V_o(1+t), где =1/273 ^oC^-1, V_o – объем при 0^oC.

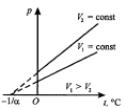
3. Процесс, происходящий при постоянном объеме, называется изохорным:

Для данной массы газа m при постоянном объеме V отношение давления p к температуре T есть величина постоянная.

p/T=const при V=const и m=const.

Кривая (Рис.2, верхний график), изображающая зависимость между p и T, характеризующая свойства вещества при постоянном объеме, называется изохорой. Если использовать температуру по шкале Цельсия, то закон можно записать в следующей форме p=p_o(1+t), где =1/273 ^oC^-1, а p_o – давление при 0^oC.

Уравнением состояния термодинамической системы называется уравнение, которое связывает давление p , объем V и температуру T термодинамической системы, находящейся в состоянии термодинамического равновесия: f(p,V,T)=0, где каждая из переменных является функцией двух других.

Уравнение состояния идеального газа:

По закону Авогадро, при одинаковых p и T один моль любого газа занимает одинаковый молярный объем V_m.

Уравнение состояния для одного моля идеального газа:

, где константа R=8,31 Дж/(моль·К) - называется универсальной газовой постоянной.

Уравнение Менделеева-Клапейрона — уравнение состояния для массы m идеального газа (т.е =m/ молей, где  – молярная масса):

Если использовать постоянную Больцмана: k=1,38 10^-23 Дж/К и R=k*N_A (N_A – число Авагадро), то уравнение состояния примет вид: , где n — концентрация молекул — число молекул в единице объема.

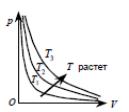
Адиабатический процесс - это процесс, происходящий без теплообмена с внешней средой. Такие процессы происходят в теплоизолированных системах. К адиабатическим процессам можно отнести все быстропротекающие процессы в не теплоизолированных системах (теплообмен не успевает совершиться). Несмотря на то, что в пределах большого объема состояние газа в этом случае не является равновесным, поведение газа в пределах достаточно малых объемов вполне можно описать уравнением адиабаты.

Найдем уравнение, связывающее параметры состояния идеального газа для адиабатического процесса.

Для этого запишем первое начало термодинамики для адиабатического процесса (4) с учетом того, что равно нулю, то:

следовательно (15).

Воспользуемся уравнением Менделеева - Клапейрона:

.

Подставим (16) в уравнение (15). Получим:

или .

Уравнение (13) преобразуем как ,

из чего следует, что

.

Или . Учитывая, что , можно записать

.

Заменив Т на , получаем соотношение

,

т.е. уравнение состояния для адиабатического процесса, называемое уравнением Пуассона.

Поскольку >1, то очевидно, что адиабата идет круче изотермы, уравнение которой pV=const

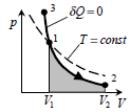
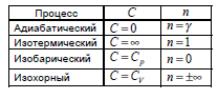
Политропический процесс – это процесс, при котором теплоемкость газа остается постоянной. pVⁿ=const При этом показатель политропы n равен

,

Рассмотренные выше изохорный, изотермический, изобарный и адиабатический процессы — это частные случаи политропного процесса.

Значения теплоемкости и показателя политропы для разных процессов приведены в таблице. Теплоемкость при изотермическом процессе бесконечно велика, поскольку dT=0.

Теплоемкость при адиабатическом процессе равна нулю, поскольку =0.