1.5 Расчет ширины спектра сигнала

Под шириной спектра понимают эффективную область частот, в пределах которой сосредоточена основная энергия сигнала.

Для ограничения спектра сигнала необходимо задаться пороговым

критерием. Из соображений, приведенных выше, порог определим как

десятую часть максимальной амплитуды гармоники. В нашем случае – это вторая гармоника.

Рисунок 1.10– Определение ширины спектра аналогового сигнала

Проанализировав график, видим, что сигнал можно восстановить по 26 гармоникам ( ₎, так как далее амплитуда не превышают десятую часть максимальной гармоники.

1.6. Восстановление сигнала усеченным рядом фурье

Восстановление сигнала определяется следующей формулой:

, где

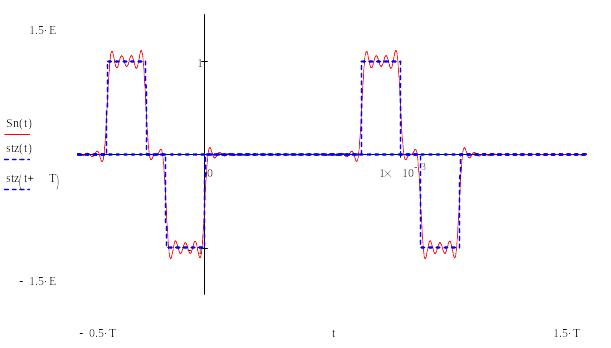
Рисунок 1.11– Восстановление аналогового сигнала усеченным рядом Фурье

Восстановленный сигнал имеет периодический, пульсирующий характер. Периодизация сигнала произошла из-за дискретизации спектральной плотности в частотной области, а пульсирует восстановленный сигнал из-за ограниченной двадцатью шестью гармониками ширины спектра сигнала.

Если восстанавливать по большему числу гармоник, то получим сигнал более похожий на исходный (рисунок 1.12).

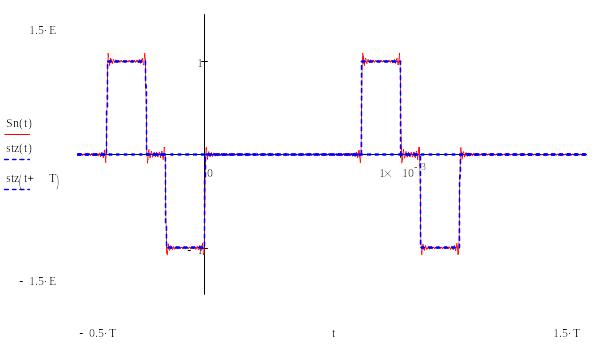
Рисунок 1.12 - Восстановление сигнала усеченным рядом Фурье по 100 гармоническим колебаниям

1.7 Расчет и построение погрешности представления аналогового периодического сигнала усеченным рядом фурье

Погрешность мощности аппроксимации оценим, как отношение разности мощностей исходного и полученного сигналов к мощности сигнала

,

Оценим мощности сигнала аппроксимированного конечным числом гармоник, как сумму мощностей каждой составляющей. Получим:

Средняя мощность сигнала равна отношению энергии периодического сигнала к периоду:

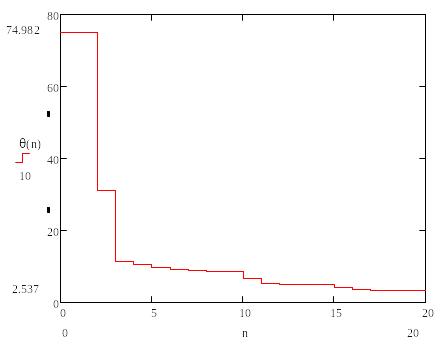
Рисунок 1.13 – Погрешность представления аналогового периодического сигнала усечённым рядом Фурье

Среднеквадратическая погрешность представления аналогового периодического сигнала усечённым рядом Фурье равна:

2. Анализ аналоговой линейной электрической цепи

1. Исходные данные

Табличное представление исходных данных:

№ варианта	№ бригады	Z1	Z2	Z3	Z4	Z5	Z6	Z7	Z8	№схемы
76	3 (26)	0	pL	R	0	pL	R	R	R	1

Рисунок 2.1 – Исходная схема аналогового фильтра

2.2 Расчет и построение частотных характеристик аналогового фильтра

Передаточной функцией называется отношение изображения выходного воздействия Y(р) к изображению входного X(р) при нулевых начальных условиях.

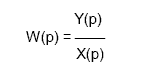
Передаточная функция является дробно-рациональной функцией комплексной переменной:

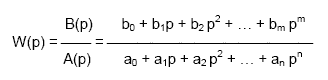
Расчет передаточной функции цепи:

1. Расчет тока I:

Представим схему в виде последовательных сопротивлений:

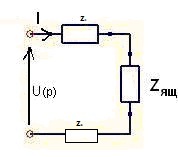
Рисунок 2.2 – Схема цепи упрощенной модели

,

Тогда выражение для тока I будет иметь следующий вид:

2. Расчет напряжения :

3. Расчет тока I₂ в ветке

4. Расчет выходного напряжения:

5. Расчет передаточной функции цепи:

6. В полученную формулу K(p) подставим свои значения:

7. Заменив , получим:

8. От операторного изображения коэффициента передачи исследуемой цепи перейдём к комплексному коэффициенту передачи , заменив в полученном выражении операторную переменную на множитель :

9. Осуществим нормировку :

Найдём выражения модуля и фазы коэффициента передачи:

Построим зависимости модуля коэффициента передачи и его фазы от частоты для аналогового фильтра-прототипа.

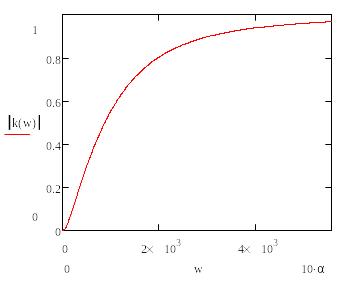
Рисунок 2.3 – Амплитудно-частотная характеристика

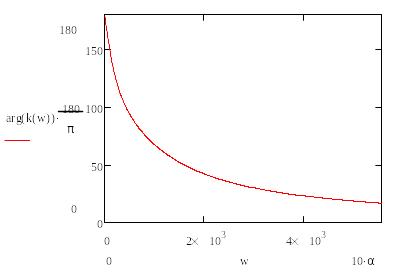
Рисунок 2.4 Фазочастотная характеристика