18.Өтпелі кезеңді есептеудің лаплас түрлендіруі.

Классикалық әдіспен есептеу кезінде функцияның бастапқы мәндерін және туындыларын табу үшін көптеген теңдеулер жүйесін шешуді қажет етеді. Осы жағдай бұл әдіспен өтпелі процесті шешуді қиындатады. Сондықтан өтпелі процесті Лаплас түрлендіруін қолданып шешу тиімді. Бұл операторлық әдіс деп аталады.

Операторлық әдістің мәні мынада: оригинал деп аталатын бірмәнді шектеулі нақты айнымалысы бар (мысалы t) f(t) функциясы берілген болсын, осы функцияға ақырғы уақыт аралығында Дирихле шартын қанағаттандыратын немесе t <0 кезінде 0-ге тең , p=s+jω кешенді айнымалының F(t) функциясы сәйкестендіріледі. Бұл функция бейне деп аталады. Бұл сәйкестендіру

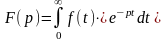
формуласы бойынша жүргізіледі және f(t) функциясы үшін Лапластың тура түрлендіруі деп аталады, былай белгіленеді:

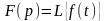
мұндағы F(t) - f(t) функциясының Лапластық бейнесі деп аталады.

Керісінше: егер берілген F(t) бейнесі арқылы f(t) оригиналын табу керек болса, онда мұны Лапластың кері түрлендіруі (Бронвич интегралы) арқылы табуға болады.

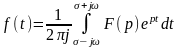
Бұл түрлендіру белгісіз f(t) функциясына салыстырмалы интегралдық теңдеудің шешімі болып табылады.

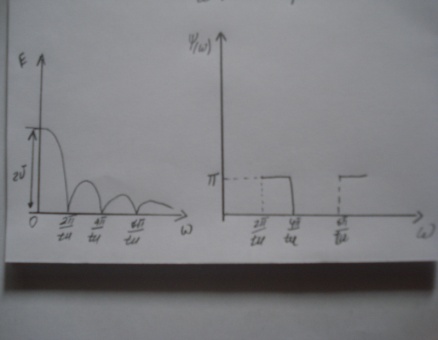
19.Периодикалық емес ф.ң спекторы. Фурьиенің тікелей түрленуін қолдану арқылы кіріс әсерлерінің спектірлерін анықтауға болады.Тікбұрышты бейнеимпульс U амплитуда және Tu ұзындығымен *1.1 сурет* тікбұрышты бейнеимпульстің спектірлік тығыздығын анықтаймыз.

*1,1*

АЖС және ФЖС *1,2*-*1,3* суретте корсетіліп келтірілген.

Периодты емес әсер етулердегі сызықты электор тізбекткрін анықтаудың спектірлік әдісі. Спектірлік әдіс кіріс сигналдарының спектірлік тығыздығын анықтауға және әсерлесу спектірлік тығыздықтың тізбек реакциасының спектірлік тығыздығын есептеуге қолданылыды.

RLC үшін бастапқы нөлдік емес шарттағы жиілікті спектірле үшін Ом заңының тізбегіне p=jw кезіндегі операторлық формадағы Ом заңынан алуға болады.

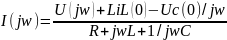
Мұнда U(jw) әсерлесу спектірлік тығыздығы.

Қатынастың бөлімі Z(jw)=R+jwL+1/jwc орнатылған гармоникалық кезеңдерді есеп/ге қолд/н тіз/ң RLC комплексті кедергісін көрсетеді.

Спектірлік әдіспен өтпелі кезеңдерді есептеудің негізгі деңгейлері.

1. F1(jw) кіріс әсерінің спек/к тығ/н анық/у.

2. Тізбек берілуінің кешенді ф/н анықтау.

3. F 2(jw) тізбегі реакцианың спектірлік тығыз/н анық/у.

4. Фурье кері түрлендіру арқ/ы және табылған f2(t) тізбек реакц/н анық/у.

20.Импульсті өтпелі сипаттаманы қолданып Дюамель интег/н жазу.

Дюамель интегралын НБШ тармақтардағы өтпелі токты, кернеуді оны кез келген ЭҚК қосқанда есептеу үшін қолданады.Тізбек реакциас/ң бірлік ұйытқуына әсер етуін, өтпелі өткізгіш фу/н g(t) н/е кернеу б/ша өтпелі фун/ны h(t) біле отырып жанама формаға әсер ететін тізбек реакциасын анықтауға болады. Әдістің негізінде Дюамель интег/ы көмегімен есептейміз. Дюамель интег/ын қолдануда, интегралдау арқылы іске асатын айнымалыны бөлуді Ʈ және тізбектегі ток анық/н уақ/ң анық/у сәтін t деп белгілейді.

T уақыттағы толық ток i(t) , U(o) g(t) ескере отырып жеке кернеу секірістерінен құралған барлық тоқтардың қосындысына тең.

I(t)=U(0)g(t)+∑u’(Ʈ)g(t-Ʈ-DƮ)DƮ (D-delta)

Өзгеру уақытының DƮ соңғы интервалын шексіз кішіге ауыстыра отырып, қосындыдан интег/ға өтуде, жазамыз

I(t)=u(0)g(t)+ʃu’(Ʈ)g(t-Ʈ)dƮ бұл Дюамель интегралы д.ат.

Дю/ль интег/ң бірнеше жазылу формасы бар.

1. I(t)=U(0)g(t)+ʃu’(Ʈ)g(t-Ʈ)dƮ

2. I(t)=u(0)g(t)+ʃu’(t-Ʈ)g(t0dt

3. I(t)=g(0)U(t)+ʃg’(t-Ʈ)U(Ʈ)dƮ

4. I(t0=g(0)U(t)+ʃg’(t)U(t-Ʈ)dƮ

5. I(t)=d/dtʃU(t-Ʈ)g(t)dƮ

6. I(t)=d/dtʃU(Ʈ)g(t-Ʈ)dƮ