1.Электр тізбегінің өтпелі кезеңі. Қоммутация заңдары.

Алғашқы еріксіз режимнен екінші еріксіз режимге өту - өтпелі кезең. Өтпелі кезең активті, пассивті элементтердегі тоқ пен кернеудің өзгеруі.

Коммутация кілттің ашылып, жабылуы.

Коммутацияның екі заңы

1 заңы: Коммутацияға дейінгі индуктивтегі ток қомутациядан кейінгі индуктивтіліктегі тоққа тең.

i_L(0_-)=i_L(0₊) ; W_M =

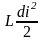
2 заңы: Коммутацияға дейінгі конденсатордағы кернеу коммутациядан кейінгі конденсатордағы кернеуге тең. U_c(0_-)=U_c(0₊);

екінші заңдылыққа сәйкес ,

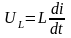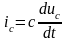
t =0 коммутация болады яғни коммутация кезі.

t(0_-) коммутацияга дейінгі уақыт

t(0₊) коммутациядан кейінгі алғашқы моменттің уақыты

t=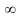 еріксіз режим д.а.

ТБШ

Екі заңдылыққа сәйкес: i_L(0_-)=i_L(0₊)=i_L(0)

U_c(0_-)=u_c(0₊)=u_c(0)

2.Өтпелі кезеннің қалыптасқан және еркін режимі.

Егер тізбек тұрақты кернеу көзіне қосылса, ток лездік мәнімен беріледі.

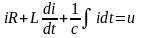
i- өтпелі ток

i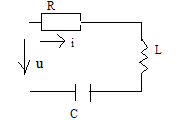 _қалR+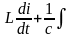 i_қалdt

i-қалыыптасқан ток

i_еркR+

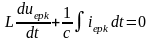
Өтпелі кернеу

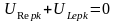
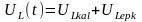
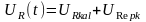
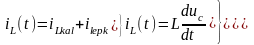Өтпелі ток

3.RL-тізбегінің өтпелі кезеңі. RL- тізбегінің қысқа тұйықталуы

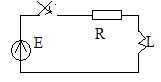U=E=const

1)Коммутацияға дейін

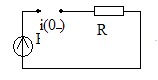i(0_-)=0 – Бастапқы шарт

2) Коммутациядан кейін

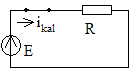i_kal= E/R

3) Өтпелі кезең

I(t)=i_қал+i_ерк , i_ерк=Ae^pt

А- интегралдау түрақтысы

p-сипаттамылық теңдеудің түбірі

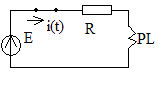
Сипаттамыл теңдеу – коммутациядан кейінгі жалпы кедергіні табу.

X_L=

Z

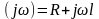
Сипаттамалық

Тендеудін түбірі

уақыт тұрақтысы

өшу коэф.

i(t)=i_қал+i_ерк=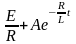 Өтпелі кезеңнің негізгі теңдеуі

RL тізбегінің қысқа тұйықталуы

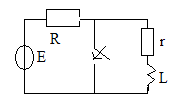
1)Коммутацияга дейн

i(0_-)=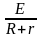

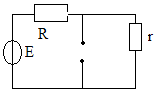
2) Коммутациядан кейн

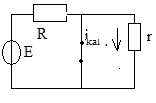
i_қал=0

3) отпелі кезең

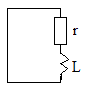
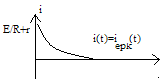
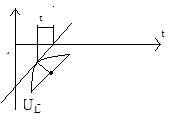
4.RL тізбегін синусоидалы кернеу көзіне қосу

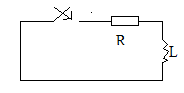
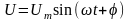
Коммутациядан кейн i_қал=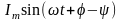

,

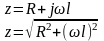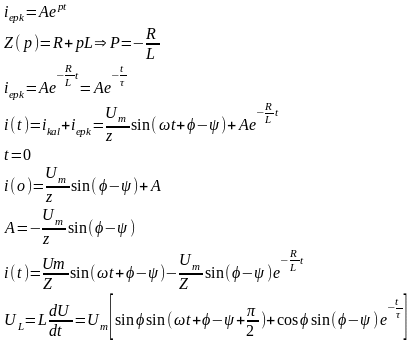
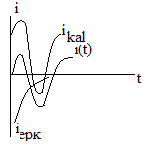
5.RC тізбегінің қысқа тұйықталуы

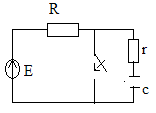
1) коммутацияга дейн ашык

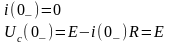
2) коммутациядан кейн жабык

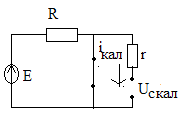
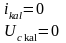
Өтпелі кезеңдегі кернеу

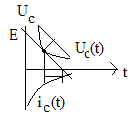
6.RC тізбегін синусоидалы кернеу көзіне қосу

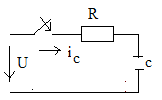
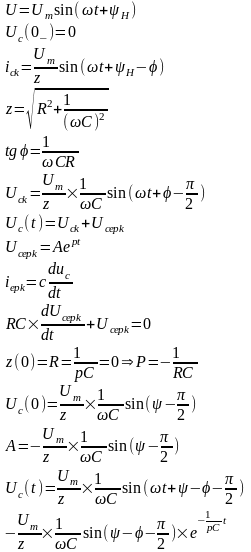
Егер 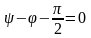болса,

онда еркін құраушысының бастапқы мәні 0-ге тең,

яғни қалыпты режим орындалады.

Егер 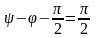болса, онда

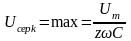
7.RLC элементтерін тізбектей қосу кезіндегі өтпелі кезең

U₀=U_R(t)+U_L(t)+U_c(t)

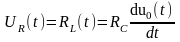
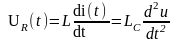
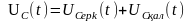
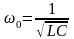
8.RLC тізбегін тұрақты кернеу көзіне қосу.

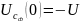переходные напряжения и ток

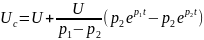
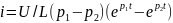
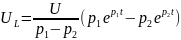
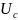кернеуі нөлден тұрақты 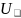кернеу көзіне дейін өседі

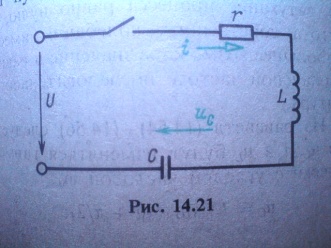
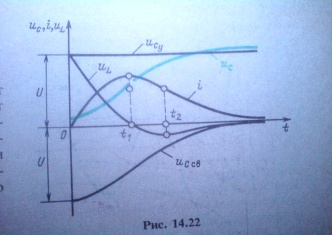
Конденсатордың аперидикалық, тербелмелі разряды

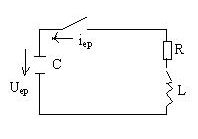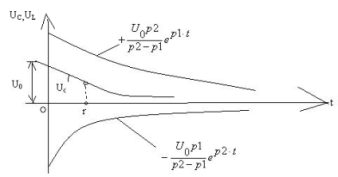
1 ) Конденсатордың аперидикалық разряды деп, резистор мен индуктивтік катушка арқылы U₀ шамасына дейін зарядталған разряды кезінде конденсатордағы кернеу U₀дан 0-ге дейін монотомды кемиді, яғни конденсатордың қайта зарядтауы жүреді.

Шарты:

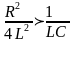немесе

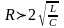
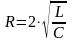критикалық кедергі.

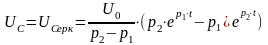
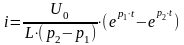
2) Конденсатордың тербелмелі разрядының шарты:

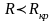
Сипаттамалық теңдеудің түбірлері комплекс сандар болу керек.

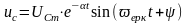
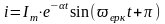
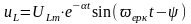
_{9.Конденсатор разрядының апериодикалық шекті жағдайы}

_{Контур кедергісі r=r (кр), яғни сипаттамалық теңдеу түбірлері тең болса, онда конденсатор разрядының апериодикалық шекті жағдайы орын алады:}

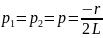дифференциал түрдегі теңдеудің жалпы шешімі мына түрде беріледі 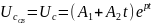еркін ток пайда болуында біз мынаны аламыз

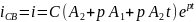сыйымдылық элементтегі кернеу және ток 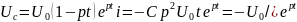және индуктивтілік элементтегі кернеу

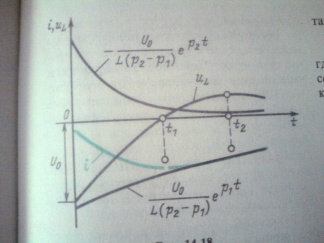
10.Сыйымдылықтың апериодикалық және тербелмелі разряды.

Егер контурлық кедергі критикалық кедергіден кіші болса r< r_кр,онда конденсатордағы кедергі периодты немесе тербелмелі разрядталады:

,

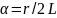Сондықтан 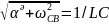. р_»,р_ә

түбірлері үшін .

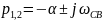Түбірлері комплекс сан кезіндегі дифференциал теңдеулерді шешу,

.

Ток

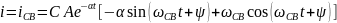
11.Операторлық түрдегі Ом және Кирхгоф заңдары.

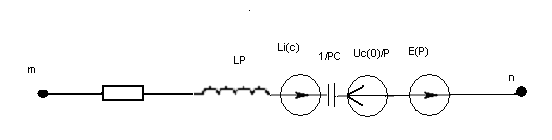
U_mn(t)=iR+L(di/dt)+1/c +U_c(0)+ e(t)

U_mn(p)= I(p)(R+pL+(1/pC))-Li(0)+(U_c(0)/p)-E(p)

I(p)= (U_mn(p)+ Li(0)- (U_c(0)/p) + E(p))/ Z(p)

Кирхгоф заңдарры

1-заңы: Түйіндегі бейнелік токтардың алгебралық қосындысы мынаған тең:

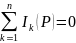
2-заңы: Тұйықталған контурдағы бейнелік кернеулердің алгебралық қосындысы сол контурдағы бейнелік ЭҚК-тердің алгебралық қосындысына тең:

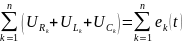
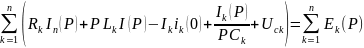
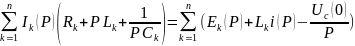
12.Дюамель интегралын қолданып өтпелі кезеңді есептеу

Беттесу әдісі бойынша:

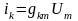
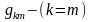өздік және 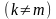өзара өткізгіштік д.а.

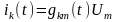
- өтпелі өткізгіштік д.а.

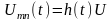
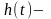кернеу бойынша өтпелі ф-я.

Мұнда кірісіндегі тұрақты кернеу U=1B беріледі.

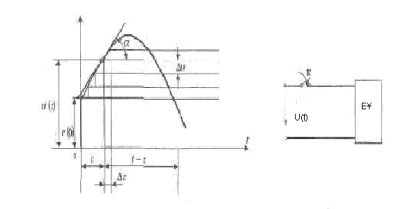
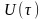кернеу көзі қосылғанда «ЕҰ» екіұшты пассив элементі берілген. Уақыт моменті t=0 болған кездегі нөлдік бастапқы шарт.

Уақыт моменті 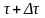секіріс болады, кернеуі

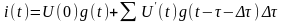
- Дюамель интегралы д.а.

13.Операторлық әдісті есептеу әдістері.

Екі түйіндік әдісті қолданамыз

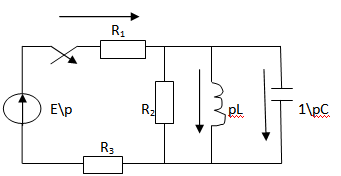Т\к: I₃(p)-?

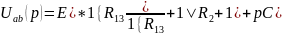
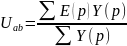
Y₁=1\R₁₃ Y₂=1\R₂ Y₃=1\pL Y₄=pC

R₁₃=R₁+R₃

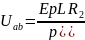
I₃(p)=U_ab(p)\pL=

Контурлық токтар әдісі

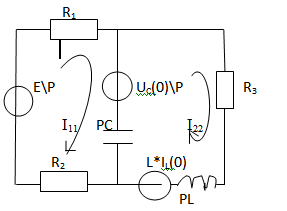
I₁₁(p)(R₁+R₂+1\pC)-I₂₂(p)(1\pC)=E\p-U_c(0)\p

-I₁₁(p)(1\pC)+I₂₂(p)(1\pC+pL+R₃)=U_c(0)\p+L*i_L(0)

∆(p)= (R₁+R₂+1\pC ) -1\pC

-1\pC (1\pC+R₃+pL)

∆(p)=p²(LC(R₂+R₁))+p(R₃C(R₁+R₂)+L)+R₁+R₂+R₃\pC

∆₁₁(p)=E\p-U_c(0)\p -1\pC

U_c(0)\p+L*i_L(0) 1\pC+pL+R₃ = p²(CLE- U_c(0)CL)+p(eR₃C+U_c(0)CR₃+L*i_L(0))+E\p²C

∆₂₂(p)=R₁+R₂+1\pC E\p-U_c(0)\p

-1\pC U_c(0)\p+L*i_L(0) = U_c(0)pC(R₁+R₂)+U_c(0) \p²C

I₁₁(p)=∆₁₁(p)\∆(p)

I₂₂(p)= ∆₂₂(p)\∆(p)

I_C(p)=I₁₁(p)-I₂₂(p)

I_L(p)=I₂₂(p)

I₁(p)=I₁₁(p)

Түйіндік потенциалдар әдісі

φ_B=0

φ_C=E\p

φ_a=(1\R₁+1\R₃+1\(R₂+pL)+pC)=-U_c(0)\p*pC

φ_a=- U_c(0)R₁R₃(R₂+pL)\p²R₁R₂LC+p(LR₃+LR₁+LR₁R₂R₃)+R₁R₂+R₁R₃+R₂R₃

I_c(p)=((φ_c- φ_a)-U_C(0)\p)*pC

I_L(p)=((φ_a- φ_b)+L*i_L(0))\pL

I₁(p)=(φ_a- φ_b)\R₁

Сонымен қоса операторлық әдісті эквивалентті генератор әдісімен шығаруға болады.