4. Выделение входов, ресурсов и затрат.

Входом является исходная информация для решаемой задачи.

К ресурсам относятся:

• электроэнергия;

• денежные средства;

• время на решение задачи;

• усилия на решение задачи.

Затраты определяются как расход ресурсов на решение задачи:

• расход электроэнергии – 0,5…1 КВт*час;

• расход денег – 850…1000 руб. (обслуживание, аппаратное и программное обеспечение, зарплата);

• расход времени – 3,5…4 часа;

• расход усилий – 2000…2500 Ккал.

5. Выделение выходов, результатов и прибыли.

Выходом является результат решения задачи (текстовый документ, схема, чертеж, результат вычисления и др.).

К результатам относится экономия денег, времени и усилий при решении задачи на компьютере.

Прибыль:

. ❒

1.3. Порядок выполнения работы

Данная лабораторная работа предполагает выполнение следующих этапов:

1. Изучить методические указания к лабораторной работе.

2. Найти множество букв: И – в вашем имени, О – в отчестве, Ф – в фамилии.

3. Найти следующие множества:

А₁ = И  О  Ф;

А₂ = И  О  Ф;

А₃ = О \ И \ Ф;

А₄ = О Δ И Δ Ф;

А₅ = = U \ А₁.

4. Сократить множество А₁ до 10 элементов, убрав из него буквы с наименьшей повторяемостью в исходном наборе букв. В результате будет получено множество вершин E.

5. Задать на полученном множестве E отношение R, представляющее собой порядок следования букв в исходном наборе без учета пробелов. Графически отобразить отношение R на множестве E.

6. Преобразовать полученное отношение в ориентированный граф G(V, E), удалив кратные дуги и петли.

7. Задать полученный граф G(V, E) перечислением дуг, с помощью матрицы смежности и матрицы инцидентности.

8. Провести системный анализ заданного объекта (табл. 1.1). Задача анализа – обеспечение нормального функционирования объекта. При проведении анализа описать следующие сведения о системе:

• цель системы;

• подсистемы и их цели;

• внешние системы;

• входы, ресурсы и затраты;

• выходы, результаты и прибыль.

9. Оформить и защитить отчет по лабораторной работе.

Таблица 1.1

Варианты систем для анализа

№ вар.	Система	№ вар.	Система
1, 11	Холодильник	6, 16	Телевизор
2, 12	Стиральная машина	7, 17	Велотренажер
3, 13	Кондиционер	8, 18	Посудомоечная машина
4, 14	Пылесос	9, 19	Мобильный телефон
5, 15	Микроволновая печь	10, 20	Принтер

1.4. Контрольные вопросы

1. Что понимают под системой при проведении анализа?

2. Что называют элементами системы?

3. Какие элементы системы называют входными и выходными?

4. Что понимают под структурой системы?

5. ?

2. Алгоритмы построения остовного дерева

2.1. Цель работы

Цель работы – приобрести умение решать задачи, связанные с построением остовных деревьев.

Работа рассчитана на 2 часа.

2.2. Основные теоретические сведения

Ориентированным остовным деревом является дерево, в котором никакие две дуги не заходят в одну и ту же вершину (рис. 2.Х). Корнем ориентированного остовного дерева называется единственная его вершина, которая не имеет ни одной заходящей дуги. Дуги такого дерева называют ветвями, а конечные вершины – листьями.

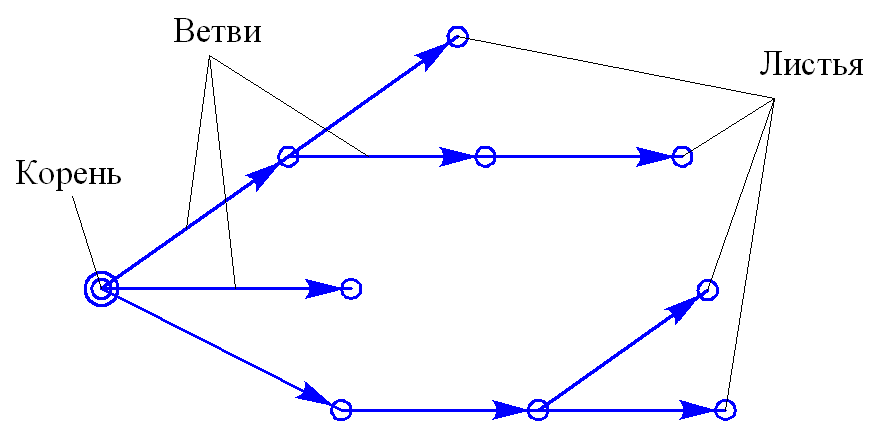
Рис. 2.Х. Схема ориентированного остовного дерева

В алгоритме используются следующие данные.

Множество исследуемых вершин (множество И) – по данному множеству массиву контролируются уже просмотренные вершины.

Основная цепь (ОЦ) – одномерный массив. Заполняется в процессе работы алгоритма. В исходном состоянии пуст (содержит нули).

Матрица векторов смежности (МВС) – двумерный массив, строки соответствуют элементам ОЦ. Каждая строка является вектором смежности для вершины, занесенной в соответствующую строку ОЦ.

Результирующая цепь (РЦ) – одномерный массив, в него заносится последовательность вершин, образующих искомую цепь, но в обратном порядке, от N1 до N2.

Оба алгоритма состоят из двух частей: прямого хода и обратного. Во время прямого хода строится совокупность векторов смежности, задающих перечень вершин, смежных с каждой из вершин графа, последовательно заносимых в основную цепь. Таким образом, основная цепь содержит перечень вершин графа, для которых строятся векторы смежности.

В процессе выполнения обратного хода по векторам смежности последовательно прослеживается, начиная от конечной вершины N2, цепь дуг, связывающая её с начальной вершиной N1.

Используемое в обоих алгоритмах понятие “очередная просматриваемая вершина” означает вершину, для которой в настоящее время ищутся смежные.

По алгоритму поиска «в глубину» сначала строится путь на максимальную глубину, то есть пока есть дуги, продолжающие путь, затем производится ветвление от конечной вершины.

Алгоритм поиска «в глубин»

Исходные данные: множество дуг, N1 - начальная вершина цепи, N2 - конечная вершина цепи.

Прямой ход.

Этап 0. Все вершины заносятся в множество И (исследуемые вершины).

1. Начальная вершина N1 заносится в основную цепь (ОЦ), в качестве очередной просматриваемой (ОП) принимается первая вершина из ОЦ.

2. Вершина ОП вычеркивается из И.

3. Выявляется очередная вершина из множества И, смежная с ОП (ВСОП).

4. Если ВСОП нет, то ОП вычеркивается из ОЦ. В качестве ОП принимается предшествующая вершина из ОЦ. Переход к П.2.

5. Если ВСОП не является искомой вершиной N2, то ВСОП помещается очередным элементом в вектор смежности вершины ОП и в основную цепь (ОЦ). Иначе - переход к П.7.

6. В качестве ОП принимается следующая вершина из ОЦ. Переход к П.2.

7. Конец прямого хода.

Обратный ход.

Обратный ход начинается от найденной вершины N2.

0. Принять в качестве вершины, заносимой в результирующую цепь (вершины ЗЦ), вершину N2.

1. Занести вершину ЗЦ в результирующую цепь. Если вершина ЗЦ является вершиной N1, то перейти к П5.

2. Выявить вершину из основной цепи (вершину О), в вектор смежности которой входит вершина ЗЦ.

3. Найти вершину О среди вершин, входящих в векторы смежности.

4. Принять вершину О в качестве вершины ЗЦ. Перейти к Э.1.

5. Переписать результирующую цепь наоборот.

6. Конец алгоритма.

Пример выполнения прямого хода алгоритма поиска “В глубину” приведен в прил. 1.

При поиске в ширину в первую очередь производится просмотр всех вершин, смежных с очередной просматриваемой, только затем поиск смещается ниже, то есть в качестве очередной просматриваемой берется первая из ранее выявленных смежных вершин.

Алгоритм поиска «в ширину».

Исходные данные: множество дуг, N1 - начальная вершина цепи, N2 - конечная вершина цепи.

Прямой ход.

0. Все вершины заносятся в множество И (исследуемые вершины).

1. В качестве очередной просматриваемой (ОП) вершины берется начальная вершина N1. Вершина ОП заносится в основную цепь.

2. Вершина ОП заносится в основную цепь. Вершина ОП вычеркивается из И.

3. Выявляются все вершины множества И, смежные с ОП (ВВСОП). ВВСОП вычеркиваются из И и заносятся в вектор смежности вершины ОП.

4. Если среди ВВСОП нет N2, то ВВСОП заносятся в ОЦ, в качестве ОП берется очередная вершина из ОЦ, переход к П.3; иначе - конец прямого хода.

Обратный ход.

Обратный ход производится аналогично обратному ходу в алгоритме поиска «В глубину».

❒ Пример 2.1. Построение ориентированного остовного дерева по алгоритму поиска «в глубину».

Требуется построить ориентированное остовное дерево на основе графа, полученного при выполнении примера 1.4 (рис. 2.Х).

Рис. 2.Х. Схема исходного ориентированного графа (пример 1.4)

Поиск цепей от начальной вершины.

Пример выполнения алгоритма поиска «в глубину» приведен в табл. 2.Х.

Таблица 2.Х

Таблица пошагового выполнения алгоритма

Шаг	V	vo	vr
1	{в, и, т, с, к, е, н, л, а}	в	и
2	{и, т, с, к, е, н, л, а}	и	т
3	{т, с, к, е, н, л, а}	т	с
4	{с, к, е, н, л, а}	с	к
5	{к, е, н, л, а}	к	–
6	{е, н, л, а}	с	л
7	{е, н, л, а}	л	а
8	{е, н, а}	а	–
9	{е, н}	л	–
10	{е, н}	с	–
11	{е, н}	т	–
12	{е, н}	и	е
13	{е, н}	е	н
14	{н}	н	–

Матрица векторов смежности

vo	vr
в	и
и	т	е
т	с	–
с	к	л	–
к	–
л	а	–
а	–
е	н
н	–

Обратные ходы по матрице векторов смежности будут:

• н ← е ← и ← в;

• а ← л ← с ← т ← и ← в;

• к ← с ← т ← и ← в.

Полученные пути можно отобразить на схеме ориентированного остовного дерева (рис. 2.Х), из которого видно, что вершина в является корнем, а вершины к, а, н – листьями дерева. ❒

Рис. 2.8. Схема ориентированного остовного дерева

Наименьшее остовное дерево – это вариант остового дерева имеющий наименьший суммарный вес ребер.

Задача построения наименьшего остового дерева решается как в качестве отдельной задачи анализа структуры системы, так и в качестве вспомогательной задачи при поиске кратчайшего пути обхода всех вершин графа (задача коммивояжера).

Общую постановку задачи построения наименьшего остового дерева можно сформулировать следующим образом:

Дан взвешенный неориентированный граф G(V, E);

D(N, N) –матрица смежности для заданного графа.

Необходимо найти вариант остового дерева, имеющий наименьший суммарный вес дуг.

Алгоритм выявления наименьшего остового дерева основан на последовательном присоединении к формируемому остовому дереву вершины графа, оказавшейся к нему (к уже сформированному остовому дереву) ближайшей.

На начальном этапе принимается, что расстояние от всех вершин графа до остового дерева равно бесконечности (остового дерева еще нет) в остовое дерево включается любая вершина графа.

Затем происходит пересчет расстояний от вершин графа до вершин остового дерева. Причем этот пересчет производится не перебором всех дуг, связывающих каждую вершину графа v_j, с вершинами уже сформированного остового дерева, а путем сравнения ранее принятого минимального расстояния от вершины v_j до остового дерева с весом дуги, связывающей вершину v_j с вершиной последней, включенной в остовое дерево, то есть с весом дуги T(v_j, v_k), Где v_k – обозначение вершины, последней присоединенной к остовому дереву.

Если вес дуги T(v_j, v_k) оказывается меньше, чем ранее принятое расстояние от вершины v_j до остового дерева, то в качестве кратчайшего расстояния от вершины графа v_j до остового дерева запоминается вес дуги T(v_j, v_k). В качестве вершины остового дерева, ближайшей к вершине графа v_j запоминается вершина v_k.

Такой принцип пересчета позволяет значительно сократить количество вычислений.

После пересчета расстояний от вершин графа до вершин остового дерева выбирается вершина, ближайшая к уже сформированному остовому дереву и принимается в качестве вершины v_k, то есть включаемой в остовое дерево. Данная вершина вычеркивается из множества вершин графа.

Можно выделить следующие этапы алгоритма:

1). Создается матрица-столбец R, в которую будут заноситься кратчайшие расстояния от вершин графа до остового дерева. В качестве начальных значений элементов матрицы R задается ∞.

Создается матрица-столбец B для хранения вершин остового дерева, ближайших к вершинам графа. В качестве начальных значений элементов матрицы B принимаются пробелы.

2). Пересчитываются расстояния от каждой вершины графа , не включенной в остовое дерево до вершин остового дерева, то есть значения элементов матрицы R по схеме:

Если R(v_j)≥T(v_j, v_k), то R(v_j)=T(v_j, v_k) и B(v_j)=v_k;

где R(v_j) – расстояние от вершины v_j до остового дерева, записываемое в матрицу R;

B(v_j) – вершина v_j остового дерева, ближайшая к вершинам графа и записываемая в матрицу B.

То есть, если расстояние R(v_j) от какой либо вершины v_j до остового дерева больше чем вес дуги между данной вершиной и вершиной v_k (вершиной включенной в остовое дерево), то в качестве расстояния R(v_j) принимается вес данной дуги T(v_j, v_k).

3). В качестве вершины v_k принимается вершина v_j с наименьшим значением R(v_j) из матрицы R, т. е. вершина ближайшая к остовому дереву. Вершина v_k вычеркивается из множества вершин.

4). Если не все вершины графа вычеркнуты, то выполняется переход к этапу 3.

❒ Пример 2.2. Построение наименьшего неориентированного остовного дерева.

Требуется найти вариант наименьшего остовного дерева для неориентированного взвешенного графа, показанного на рис. 2.Х.

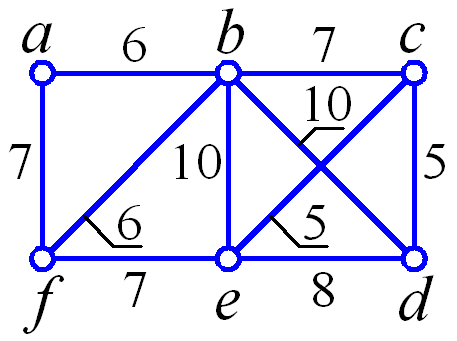
Рис. 2.Х. Схема исходного графа

Матрица смежности для заданного графа имеет следующий вид:

i, j	a	b	c	d	e	f
a	∞	6	∞	∞	∞	7
b	6	∞	7	10	10	6
c	∞	7	∞	5	5	∞
d	∞	10	5	∞	8	∞
e	∞	10	5	8	∞	7
f	7	6	∞	∞	7	∞

В качестве вершины v_k, то есть вершины, помещаемой в остовое дерево принимается любая вершина, пусть это будет первая вершина - а Вычеркнуть вершину v_k из вершин графа.

В результате получим вариант остовного дерева, схема которого показана на рис. 2.Х. ❒

Рис. 2.Х. Схема варианта наименьшего остовного дерева