1.2.3. Декартово произведение множеств. Соответствия и отношения на множествах

Кортежем (упорядоченным множеством) длины n называют совокупность элементов a₁, a₂, … , a_n , которая в отличии от множества {a₁, a₂, … , a_n} характеризуется порядком входящих в эту совокупность элементов, то есть каждый элемент занимает определенное место.

При n=2 кортеж называется упорядоченной парой, при n=3 – упорядоченной тройкой, при n=4 – упорядоченной четверкой и т. д.

Декартовым (прямым) произведением множеств A₁, A₂, … ,A_n называется множество A₁×A₂×…×A_n, состоящее из всех кортежей длины n на множествах A₁, A₂, … , A_n.

Если A₁=A₂=…=A_n=А, то декартово произведение множеств A₁, A₂, … , A_n называют декартовой степенью множества А и обозначают через Аⁿ.

При n=2 А² называют декартовым квадратом, а при n=3 А³ называют декартовым кубом. По определению полагают, что А¹=А, А⁰={λ}, где {λ} – одноэлементное множество, состоящее из пустого кортежа λ.

Декартово произведение множеств обладает следующими свойствами:

1) А×В ≠ В×А;

2) А×(В×С) ≠ (А×В)×С;

3) А^m×Аⁿ ≠ А^m+n;

4) A×Ø = Ø×A = Ø;

5) А×(В  С) = (А×В)  (А×С);

6) А×(В  С) = (А×В)  (А×С).

Бинарным соответствием из А в В называется всякое подмножество Р декартова произведения А×В, то есть Р А×В. При этом множество А называется множеством отправления соответствия Р, а В – множеством прибытия соответствия Р.

Элементы множества отправления, для которых соответствие установлено, называется областью определения соответствия. Элементы множества прибытия, поставленные в соответствие элементам множества отправления, называются областью значений соответствия.

Соответствие Р может быть представлено графически в виде схемы, на которой элементы множеств А и В изображаются точками, а упорядоченные пары в виде стрелок, направленных от элементов множества отправления к элементам множества прибытия (рис. 1.4).

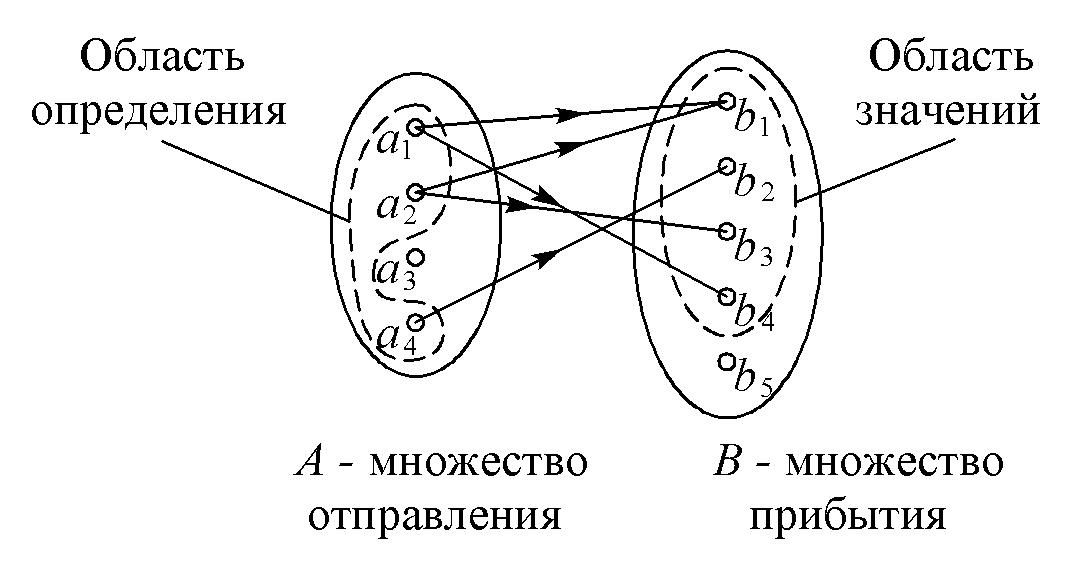
Рис. 1.4. Графическое представление соответствия

Бинарным отношением на множестве А называется всякое подмножество R декартова квадрата А², то есть R А².

Если x, y R, где R – бинарное отношение на множестве А, то говорят, что элемент находится в отношении R к элементу y и записывают это через xRy.

В общем случае n-арным отношением на множестве A называется всякое подмножество R декартовой степени n на множестве A, то есть R Aⁿ.

❒ Пример 1.3. Задание отношения на множестве.

Определим бинарное отношение следования R на множестве букв в ФИО из примера 1.1, записанных без пробела.

Исходное слово в этом случае будет:

витвитскийевгенийвладиславович

Для упрощения задания сократим количество букв до 10, удалив буквы с наименьшей повторяемостью. Для этого рассчитываем повторяемость букв (табл. 1.1):

Таблица 1.1

Определение числа повторяющихся букв

№	1	2	3	4	5	6	7	8	9	10	11	12	13
ai	в	и	т	с	к	е	г	л	н	а	д	о	ч
ni	6	8	2	4	1	2	1	2	1	2	1	1	1

Таким образом, можно удалить буквы г, д, о, ч, имеющие наименьшую повторяемость.

Результирующее слово запишется следующим образом:

витвитскийевенийвлаиславви

Отсюда отношение следования будет:

R = {<в,и>, <и,т>, <т,в>, <в,и>, <и,т>, <т,с>, <с,к>, <к,и>, <и,и>, <и,е>, <е,в>, <в,е>, <е,н>, <н,и>, <и,и>, <и,в>, <в,л>, <л,а>, <а,и>, <и,с>, <с,л>, <л,а>, <а,в>, <в,в>, <в,и>}. ❒