2.2.3. Метод парных сравнений

Метод парных сравнений часто используется при экспертизе вариантов сложных проектов, здесь трудоемкая процедура ранжирования n вариантов заменяется многократным применением более простой процедуры попарного сравнения вариантов между собой. Достоинства этого метода особенно проявляются при большом числе вариантов n.

Пусть сравниваются два варианта v_p и v_q, из множества V и вариант v_p по заданным критериям предпочтительнее варианта v_q. Отношение предпочтения будем обозначать v_p v_q.

В ходе экспертизы каждый i-ый эксперт заполняет таблицу, в нее он заносит результаты парных сравнений, образующие матрицу Z_i размером n × n:

; (i = 1, 2, … , m)

где

(5.12)

Матрица Z_i обладает следующими свойствами:

1. По главной диагонали стоят знаки «–» (прочерк).

2. Если элемент z_pqi = 1, то z_qpi = 0.

3. Число парных сравнений вариантов равно числу сочетаний из n по 2:

. (5.13)

Третье свойство используется для проверки правильности заполнения матрицы i-м экспертом:

. (5.14)

Эксперту рекомендуется следующий порядок заполнения Z_i. Сначала следует попарно сравнивать вариант v₁ с v₂, … , v_n т. е. заполнять первую строку матрицы Z_i. Далее вариант v₂ с v₃, … , v_n и т. д. То есть достаточно записать значение z_pqi лишь выше главной диагонали. Другая часть матрицы заполняется на основе второго свойства.

В результате работы m экспертов заполняется m таблиц Z_i парных сравнений. Обработка результатов экспертизы начинается с объединения этих таблиц в одну обобщенную матрицу размером n × n:

; (i = 1, 2, … , m),

Элементы g_pq матрицы G получаются суммированием соответствующих элементов матриц Z_i, то есть:

. (5.15)

На основе найденных значений элементов g_pq матрицы G вычисляются суммы элементов строк P_p и столбцов Q_q:

; .

Матрица G должна удовлетворять следующим условиям:

1. Сумма элементов g_pq матрицы G равна:

. (5.16)

2. При полном согласии мнений экспертов в ячейках g_pq = m, в остальных g_pq = 0.

3. При минимальном согласии мнений экспертов каждый элемент g_pq матрицы G равен m/2, если число экспертов m – четное, и равен (m + 1)/2, если число m – нечетное.

4. Сумма из элементов k-го столбца и k-ой строки матрицы G постоянна, то есть:

, (k = 1, 2, … , n). (5.17)

Коэффициент конкордации W, характеризующий согласованность мнений экспертов, для метода парных сравнений определяется следующим образом:

; (5.18)

; (5.19)

где C(2/g_pq) – число сочетаний из g_pq по 2, здесь g_pq – элемент матрицы G, при этом

(5.20)

В методе парных сравнений коэффициент конкордации W может находиться в пределах от W_min (минимальное согласие экспертов) до 1 (полное согласие).

Значение W_min определяется следующим образом:

(5.21)

Оценка значимости коэффициента W (существенно ли он отличается от W_min) производится с использованием критерия χ² Пирсона. Для этого рассчитывается оценка критерия по результатам экспертизы:

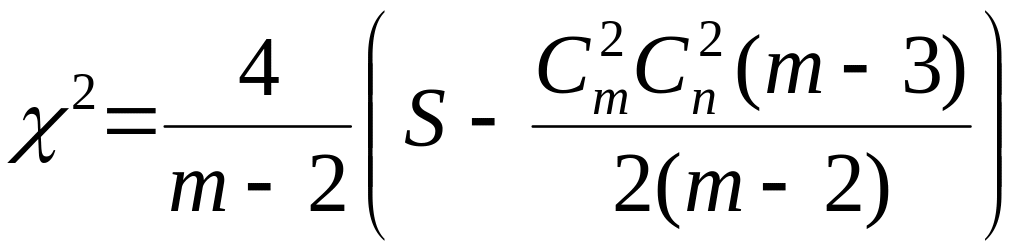, (5.22)

и число степеней свободы

. (5.23)

где значение S определяется по формуле (5.19).

Значение χ² сравнивается с табличным , определяемым по числу v и уровню значимости α (обычно 100·α = 1% или 100· = 5%).

Если χ² > , то гипотеза о значимости коэффициента W (согласованности мнений экспертов) принимается, в противном случае (χ² ) – отвергается.

Для выбора лучшего варианта необходимо определить рейтинги каждого варианта. По методу парных сравнений рейтинги вариантов вычисляются следующим образом:

; (j = 1, 2, … , n) (5.24)

где P_j – сумма элементов строки матрицы G для j-го варианта.

Наиболее предпочтительным будет являться варианта с наибольшим значением R_j.

❒ Пример 5.3. Обработка результатов экспертизы с помощью парных сравнений.

Требуется с помощью метода парных сравнений обработать результаты экспертизы (число экспертов m = 4, число вариантов n = 6), представленные в табл. 5.4 – 5.7.

Таблица 5.4

Матрица парных сравнений Z₁ для 1-го эксперта (i = 1)

vj	v1	v2	v3	v4	v5	v6
v1	–	1	0	0	1	1
v2	0	–	0	1	0	0
v3	1	1	–	0	1	0
v4	1	0	1	–	1	1
v5	0	1	0	0	–	0
v6	0	1	1	0	1	–

Таблица 5.5

Матрица парных сравнений Z₂ для 2-го эксперта (i = 2)

vj	v1	v2	v3	v4	v5	v6
v1	–	1	0	0	1	1
v2	0	–	1	1	0	0
v3	1	0	–	0	0	0
v4	1	0	1	–	1	1
v5	0	1	1	0	–	1
v6	0	1	1	0	0	–

Таблица 5.6

Матрица парных сравнений Z₃ для 3-го эксперта (i = 3)

vj	v1	v2	v3	v4	v5	v6
v1	–	1	0	0	0	1
v2	0	–	0	1	0	0
v3	1	1	–	0	1	0
v4	1	0	1	–	1	1
v5	1	1	0	0	–	1
v6	0	1	1	0	0	–

Таблица 5.7

Матрица парных сравнений Z₄ для 4-го эксперта (i = 4)

vj	v1	v2	v3	v4	v5	v6
v1	–	1	0	0	0	1
v2	0	–	1	1	0	0
v3	1	0	–	0	1	0
v4	1	0	1	–	0	1
v5	1	1	0	1	–	0
v6	0	1	1	0	1	–

Обобщенная матрица G, полученная путем суммирования элементов матриц Z₁ – Z₄ представлена в табл. 5.8, где дополнительно найдены суммы элементов в каждой строке.

Таблица 5.8

Обобщенная матрица парных сравнений G

vj	v1	v2	v3	v4	v5	v6	Pj
v1	0	4	0	0	2	4	10
v2	0	0	2	4	0	0	6
v3	4	2	0	0	3	0	9
v4	4	0	4	0	3	4	15
v5	2	4	1	1	0	2	10
v6	0	4	4	0	2	0	10

Предварительно найдем для заданных m и n числа сочетаний и :

= 4(4 – 1)/2 = 6;

= 6(6 – 1)/2 = 15.

Для оценки согласованности мнений экспертов определим по формулам (5.18) и (5.19) коэффициент конкордации W и число S. Для этого по формуле (5.20) найдем число C(2/g_pq) сочетаний для каждой пары вариантов (табл. 5.9).

Таблица 5.9

Таблица чисел сочетаний C(2/g_pq)

vj	v1	v2	v3	v4	v5	v6
v1	0	6	0	0	1	6
v2	0	0	1	6	0	0
v3	6	1	0	0	3	0
v4	6	0	6	0	3	6
v5	1	6	0	0	0	1
v6	0	6	6	0	1	0

Сложив значения в табл. 5.9, получим S = 72.

Отсюда значение коэффициента W будет:

.

Определим по формуле (5.21) наименьшее значение коэффициента конкордации W_min. Поскольку число экспертов четное (m = 4), то значение W_min будет:

W_min = (4 – 2)/[2(4 – 1)] = 0,33.

Следовательно, значение коэффициента W находится в допустимом интервале 0,33…1.

Оценим значимость коэффициента W по критерию χ² Пирсона.

Оценка критерия χ² по формуле (5.22) будет:

.

Число степеней свободы найдем из формулы (5.23):

.

Табличное значение (см. табл. П.1) при уровне значимости α = 0,05 и v = 45 будет = 1,36·45 = 61,2.

Поскольку , то

Рейтинги вариантов по формуле (5.24) будут:

; ;

; ;

.

Таким образом, наибольший рейтинг по согласованному мнению экспертов имеет вариант v₄. ❒