12. Модель Мертона для оценки корпоративных ценных бумаг.
Корпоративные ценные бумаги – ценные бумаги, выпущенные корпорациями. В России – это ценные бумаги, выпущенные ОАО (так как у нас нет корпораций). Основная особенность – a корпоративные ценные бумаги нельзя учитывать без риска дефолта.
Предположим, что в момент t фирма выпустила 2 ценные бумаги: 1. обыкновенную акцию и 2.облигацию с нулевым купоном с номиналом F, датой погашения T (T>t).
Моделью Мертона предполагается, что вплоть до момента погашения облигации дивиденды не выплачиваются, издержки реорганизации в случае дефолта равны нулю.
В
любой момент
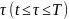выполняется равенство:
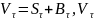– рыночная цена активов в τ,
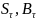– рыночная стоимость акции и облигации
в τ.
В
момент погашения облигация будет стоить:
;
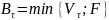акция:
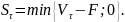
Арбитражных
возможностей нет, поэтому цена акции в
любой момент
совпадает со стоимостью
европейского «колл» с ценой исполнения
F, дата исполнения T:
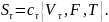
Рассмотрим
.
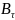Значит
в любой момент τ стоимость
облигации должна совпадать со стоимостью
инвестиционного портфеля, состоящего
из инвестиции
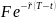под
на T-t лет и
европейского «пут» с ценой исполнения
F и датой истечения T.
Тогда
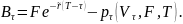
Пусть выполняются все условия модели Блэка-Шоулза:
Рынки совершенны и торговля на них ведется непрерывно во времени
Существует безрисковая процентная ставка, она не изменяется во времени и одинакова для всех сроков
Стоимость активов фирмы определяется геометрическим броуновским движением
,
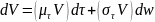то есть
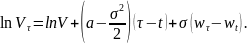
Тогда
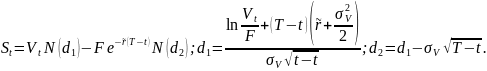
Введем
новое обозначение:
–
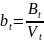доля заемных средств в капитале фирмы
Тогда
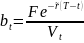—оценка
доли заемных сркдств в капитале фирмы
или «квази доля».
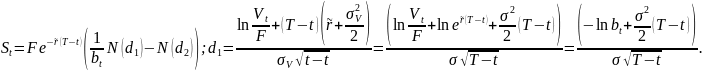
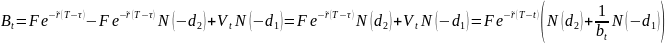
Проблема: практически невозможно оценить стоимость активов и не ясно как найти волатильность.
Чтобы оценить недостающие параметры, зная в текущий момент стоимость акций и волатильность, можно воспользоваться формулой Ито:
Решить
такую систему будем численными методом.
Задача минимизации
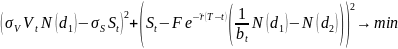
Модель Ваcичека
Однофакторная математическая модель, описывающая эволюцию Краткосрочной (мгновенной) процентной ставки. Модель предложена Олдричем Васичеком в 1977 году. Однофакторность связана с тем, что в модели участвует лишь один источник неопределенности динамики ставки
Предположим,
что краткосрочная безрисковая процентная
ставка
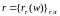определяется сттхаст диф уравнением
вида
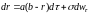(1)
(процесс Орнштейна Уленбека), где
-
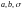некоторые положительный числа, при
некотором начальном условии
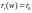(2)
Теорема
Если
краткоср. безриск. проц.ст.
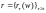удовлетворяет (1) и (2), то
Доказательство
ЧТД.
Недостаток:
,
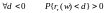т.е. теоретические ставки могут быть
отрицательными
Свойства:
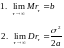
Из свойств следует, что существует долгосрочное среднее процентной ставки, таким образом модель учитывает эффект возвращения к среднему
Теорема
В
условиях модели Васичика при постоянной
рыночной цене риска
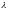стоимость
облигации с нулевым купоном единичного
номинала без дефолт-риска вычисляется
по формуле:
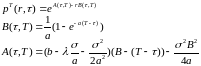
Доказательство
Доказательство
основывается на общей теореме:
Теперь к самому доказательству
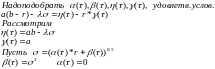
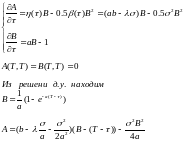
Нет никакой гарантий, что в данной модели теоретическая доходностей совпадет с рыночной.