Модель Блэка-Шоулса для оценки европейских опционов
Выполняются следующие условия:
Рынки ЕО и спот-рынок совершенны
Можно неограниченно брать ссуды и кредитовать под соответствующую (по срокам) безрисковую процентную ставку
Исходные активы обладают постоянной непрерывной дивидендной доходностью , а их цена определяется ГБД
,
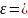где
На рынках отсутствуют прибыльные арбитражные возможности.
Теорема:
если с
и р –
текущие цены ЕО «колл» и «пут» на активы
с постоянной дивидендной доходностью
,
годовая волатильность которых равна
,
то в условиях модели Блэка-Шоулса:
Доказательство:
На временном промежутке (T-t) можно рассмотреть n–этапную биномиальную модель с параметрами:
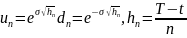
Тогда стоимость ЕО «колл» по теореме Кокса-Росса-Рубенштейна:
)
Где
)
и
-
вероятности того, что в n
независимых испытаниях число успехов
окажется больше или равно k,
если вероятность успеха в одном испытании
равна
и
соответственно.
Так
как последовательность случайных
процессов
,
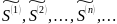определяемых биномиальными моделями,
слабо сходится к ГБД
,
)
)}=
)}=
Для «пута» воспользуемся паритетом цен ЕО:
11. Дельта и гамма хеджирование опционных позиций.
В
общем случае стоимость производного
финансового инструмента зависит от
следующих факторов:
Дельта-коэффициент—это
производная
.
Свойства:
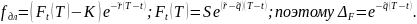
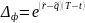
В модели Блэка-Шоулза:
Американский опцион.
.
Хеджирование.
Рассмотрим портфель инструментов, производных от одних и тех же базовых активов. Покупая, продавая такие инструменты можно дельта-нейтрализовать портфель.
Пусть
-
дельта-коэффициент портфеля,
-
дельта-коэффициент биржевого инструмента,
производного от данных финансовых
активов.
Х-количество
покупаемых (если X>0) или
продаваемых (если X<0).
Процедура дельта-хеджирования:
Выбираем производный инструмент от тех же базовых инструментов, из каких состоит портфель.
Портфель дельта-нейтрализуем.
Периодически ребалансируем данный портфель, чем чаще ребалансировка происходит, тем хеджирование лучше. Но стоит помнить о том, что увеличиваются транзакционные издержки.
И так до момента истечения контракта.
Гамма-коэффициент
– это производная:
При
изменении базового актива на величину
,
при неизменных прочих
равна
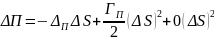
Свойства:
1.
2.
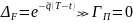
3. Гамма-коэф европейского пут и колл
Хеджирование.
Рассмотрим портфель, производный от одних и тех же базовых активов. Гамма-коэффициент-это линейная комбинация гамма-коэффициентов инструментов, входящих в портфель (с «+», если позиция длинная, с «-», если короткая).
Портфель
будем называть дельта-гамма нейстральным,
если
Основное свойство дельта-гамма
нейтрального портфеля – при изменении
цены базового актива на величину
и неизменности остальных факторов:
.
Для нейтрализации надо решить систему:
Х и у – количество покупаемых инструментов первого и второго вида.
Процедура гамма-хеджирования:
Выбрать 2 биржевых инструмента, чтобы дельта-гамма нейтрализировать.
Периодически ребалансировать позицию, то есть покупая или продавая выбранные инструменты нужно добиться дельта-гамма нейтральности портфеля вплоть до даты истечения