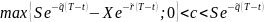8. Валютный своп и его оценка

В стандартном валютном свопе предусматривается обмен процентных платежей по фиксированной процентной ставке от условной денежной суммы в одной валюте на поток процентных платежей по фиксированной процентной ставке от условной денежной суммы в другой валюте.

В валютном свопе в отличие от процентного в момент окончания действия свопа производится также обмен основными суммами.

Пусть компания А согласилась получать процент по ставке q₁(m) от денежной суммы Q1 в одной валюте, а платить по ставке q₂(m) от денежной суммы Q2 во второй валюте.

Предполагается, что отсутствует риск дефолта.

Оценка стоимости свопа: предполагается, что своп эквивалентен портфелю облигаций –

1. покупка облигации номиналом Q1 (в первой валюте) с купонной ставкой q₁(m), купоны по которой выплачиваются m-раз в год.

2. Продажа облигации номиналом Q2 (во второй валюте) с купонной ставкой q₂(m), купоны по которой выплачиваются m-раз в год

Стоимость первой облигации В₁(t), стоимость второй облигации В₂(t)

Тогда стоимость валютного свопа определяется как: V_t = В₁(t) - c_tВ₂(t) – оценка в первой валюте

Для оценки стоимости В₁(t) можно использовать временную структуру безрисковых процентных ставок в стране с первой валютой (В₂(t) – аналогично для страны со -2й валютой)

B₁(t) = 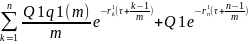, r¹_k – безрисковая процентная ставка в певой стране на срок τ +

B₂(t) =

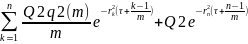
Стоимость свопа может быть как положительной, так и отрицательной.

Другой способ оценки валютного свопа: представление свопа в качестве последовательности потока платежей по форвардному контракту

Рассмотрим форвардный контракт на обменный курс в объеме 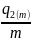Q2 с ценой поставки 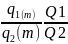. В данном контракте необходимо занять короткую позицию.

Тогда первый обмен платежами в валютном свопе будет эквивалентен платежу по форвардному контракту.

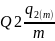
Стоимость короткой позиции: 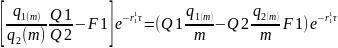– приведенная стоимость первого обмена платежами.

В любой момент τ + k=1,…,n-1 стоимость обмена платежами следующая:

( , в момент τ + :

Тогда V(t) =

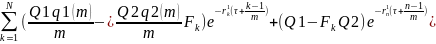
F_k - форвардный обменный курс. F_k = с_t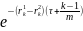

c_t - стоимость второй валюты в единицах первой валюты

9. Опционы и их основные характеристики. Паритет цен европейских опционов.

Европейский опцион «колл» («пут») – предоставляет его держателю право купить (соответственно, продать) определенное количество некоторых активов по заранее установленной цене (цене исполнения) в момент истечения срока контракта (дата истечения опциона).

Американский опцион «колл» («пут») - предоставляет его держателю право купить (соответственно, продать) определенное количество некоторых активов по заранее установленной цене (цене исполнения) в любое время вплоть до момента истечения срока контракта (дата истечения опциона).

Момент, когда фактически производится покупка или продажа активов, предусмотренная опционом, называется моментом исполнения опциона. У европейских опционов момент исполнения и дата истечения совпадают. У американских момент исполнения может наступать до даты истечения.

Держатель опциона занимает длинную позицию в опционном контракте, а сторона выпустившая или подписавшая опцион, - короткую позицию. Сторона с длинной позицией имеет право выбора совершить или не совершить операцию по покупке, а сторона с короткой позицией обязана выполнить соответствующую операцию по требованию стороны с короткой позицией.

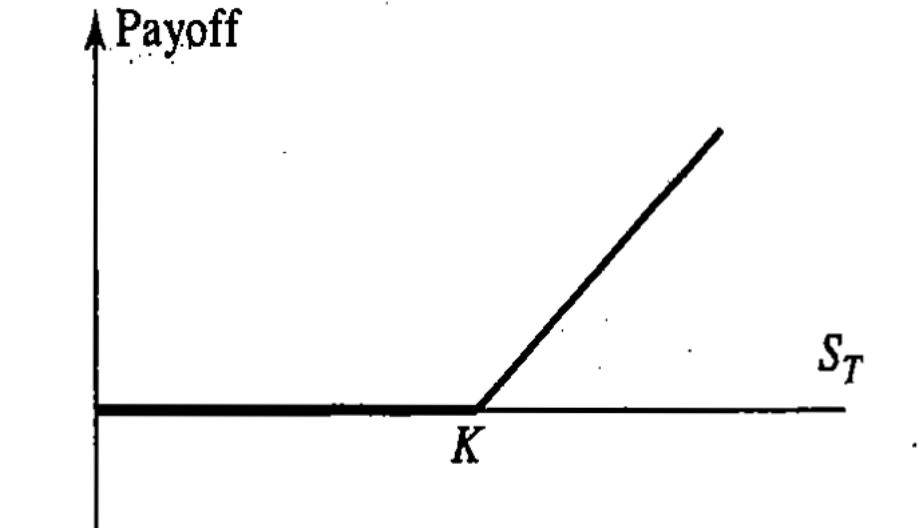
Рассмотрим выигрыш стороны с длинной позицией в европейском опционе «колл» на момент его исполнения:

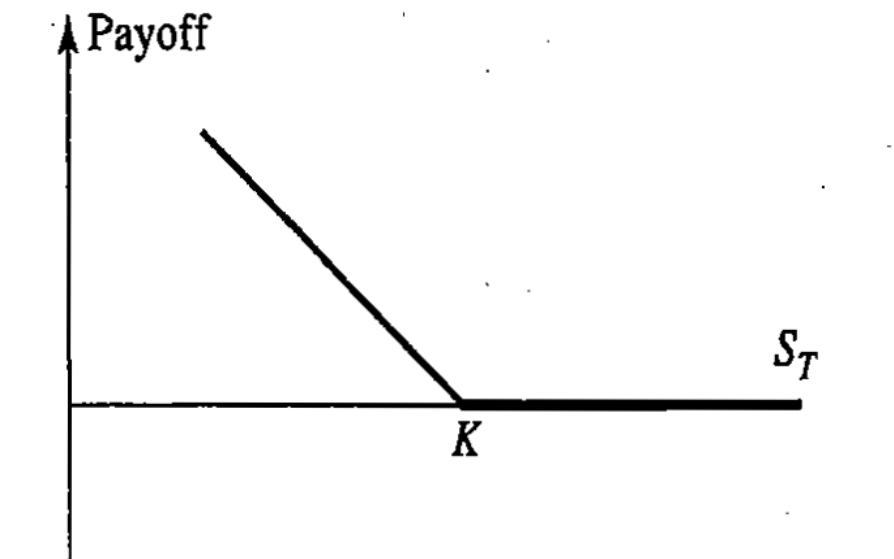
Выигрыш держателя европейского опциона «пут»:

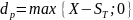
Паритет цен европейских опционов

Существуют спот-рынок и рынок ЕО для одних и тех же активов. Выполняются следующие условия:

1. Рынки совершенны

2. Неограниченно можно брать ссуды и кредитовать под соответствующую (по срокам) безрисковую процентную ставку

3. Отсутствуют прибыльные арбитражные возможности

Теорема: Если c и p – стоимости ЕО «колл» и «пут» на одни и те же активы с ЦО Х, дата истечения которых Т , то имеет место паритет цен :

- цена исходных активов в текущий момент t

– приведенная стоимость доходов, поступающих от исходных активов за время от t до T

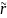– безрисковая процентная ставка на срок (T-t) лет при непрерывном начислении.

Доказательство:

Рассмотрим два портфеля

Портфель А: длинная позиция в ЕО «колл» и инвестиции денежной суммы под на (T-t) лет.

Портфель В: длинная позиция в ЕО «пут» и покупки исходных активов.

Тогда начальные затраты от А и В: соответственно

Доходы на момент Т:

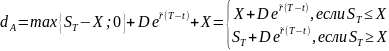
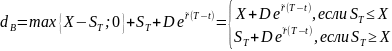
Т.к. доходы совпадают, то при отсутствии прибыльных арбитражных возможностей должны совпадать и начальные затраты, то есть:

Следствие: Текущие цены ЕО «колл» и «пут» на исходные активы с ЦО 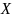, дата истечение которых Т, должны удовлетворять следующим неравенствам:

Теорема: Если c и p – стоимости ЕО «колл» и «пут» на одни и те же активы с постоянной непрерывной дивидендной доходностью 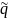,с ЦО Х, дата истечения которых Т , то имеет место паритет цен :

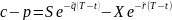
Доказательство:

Портфель А: покупка ЕО «колл» и инвестиции денежной суммы под на (T-t) лет.

Портфель В: покупка ЕО «пут» и покупка единиц исходных активов.

Т.к. доходы совпадают, то при отсутствии прибыльных арбитражных возможностей начальные затраты совпадают:

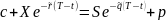
Следствие: Текущие цены ЕО «колл» и «пут» на исходные активы с ЦО , дата истечение которых Т, должны удовлетворять следующим неравенствам: