Оценка стоимости свопового контракта:

Р

A

r_ф(m)

ρ(m)

ассмотрим процентный своп, в котором компания А готова получать фиксированную процентную савку в обмен на рыночную процентную ставку от суммы Q. Платежи осуществляются m-раз в год.

Q

Ч

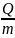r_ф(m) - ρ₁(m)

r_ф(m) - ρ₀(m)

r_ф(m) - ρ_N-1(m)

истый поток платежей компании А в момент t:

τ + 1/m 1/m+

τ + N-1/m 1/m+

t

………..

τ 1/m

τ – число лет до очередного обмена платежами (0<τ<1/m)

Стратегия, обеспечивающая такой поток платежей:

1. Покупка облигации с купонной ставкой r_ф(m) номиналом Q с оплатой купонов m-раз в год, если остается n купонных платежей

2. Продажа облигации номиналом Q с плавающей процентной ставкой ρ(m)

Отличие: последний платеж по имеющейся облигации будет номинал Q, но так как другая облигация с таким же номиналом была продана, то эту же сумму Q нужно будет выплатить, в результате –взаимозачет.

Таким образом, построенная стратегия дает тот же поток платежей, что и процентный своп, следовательно, стоимость свопа для компании А и стоимость портфеля облигаций должны совпадать при отсутствии арбитражных возможностей:

V(t)=B1(t) – B2(t), где V(t) – стоимость свопа, B1(t) – стоимость облигации с фиксированной купонной ставкой, В2(t) – стоимость облигации с плавающей купонной ставкой.

Для определения стоимости свопа нужно знать временную структуру ставок дисконтирования при непрерывном начислении: z₁ – ставка дисконтирования на τ - лет, z₂ – ставка дисконтирования на τ +1/m - лет, z_k – ставка дисконтирования на τ + k-1/m – лет и т.д.

Тогда B1(t) = 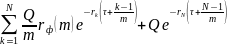, B2(t) = (Q+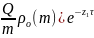

Для нахождения подходящей временной структуры процентных ставок, используем таблицу для своповых процентных ставок:

Таблица 3

Период	Своповая процентная ставка
1	rсв(1)
2	rсв(2)
…	…
N	rсв(N)

В начальный (нулевой момент) стоимость облигации равна номиналу. Каждая строка таблицы дает купонную ставку облигации имеющей стоимость, которая равна номиналу.

Из этой таблицы можно найти подходящие ставки y₁, y₂, …,y_N на сроки 1/m,2/m,…,(N-1)/m.

Например: y₁ = m*ln(1+ ),

Зная y₁, можно найти y₂:

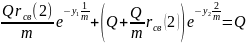и также можно найти остальные процентные ставки y₃, …,y_N.

Ставки же z₁, z₂, …, z_N можно найти с помощью кривой рыночных доходностей, используя метод интерполяции:

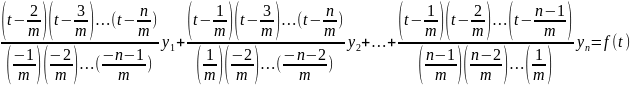
z₁ = f(τ), z₂ = f(τ + 1/m)

Этот способ оценки основан на представлении свопа в виде портфеля из двух облигаций.

Есть другой способ – представление процентного свопа как последовательности соглашений о форвардной процентной ставке FRA:

Пусть τ – момент первого обмена платежами, тогда чистый обмен: 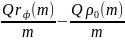(нет неопределенности), нужно продисконтиовать и получим приведенную стоимость первого платежа

Приведенная стоимость первого обмена:

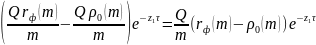
k-й обмен платежами по контракту:

Рассмотрим FRA с контрактной ставкой r_ф(m) на сумму Q/m . Занимаем короткую позицию в FRA со сроком (τ + (k-1)/m)*( τ + k/m). Стоимость позиции:

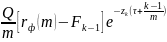- приведенная стоимость К-го обмена платежами в своповом контракте.

Тогда стоимость процентного свопа: Vt =

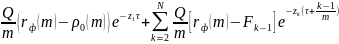
Где F_k-1 – предполагаемая форвардная процентная ставка на период от 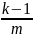τ+ до τ+

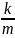
С

ρ(m)

помощью процентных свопов можно проводить хеджирование процентного риска. Доказательство основано на эффективной дюрации.

А

Qсв

r_ф

Допустим, есть кредит суммой Qкр на срок Т, для хеджирования процентного риска необходимо заключить процентный своп на срок, равный кредиту.

Было доказано, что процентный своп эквивалентен портфелю из облигаций. Для него можно вычислить эффективную дюрацию в зависимости от потока платежей:

В моменты τ, τ + 1/m, τ + 2/m, …, τ +(n- 1)/m

Платежи: Qсв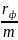 , Qсв ,…,Qсв + Q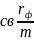

Поступления компании Qсв + Qсв , -, - , -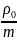

Складываем 2 потока и получаем: -Q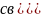 + Qсв , -Q ,… , -Q , -Qсв - Q

Обозначим эти платежи за С1, С2, …, Cn

В результате имеем инструменты с фиксированными доходами

Dэф = 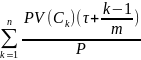– это необычная дюрация т.к. поток платежей заменен на эквивалентный

PV(Ck) = Ck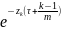

D эф – может быть как больше так и меньше нуля

По кредиту также есть дюрация исходя из потока платежей:

В моменты τ, τ + 1/m, τ + 2/m, …, τ +(n- 1)/m

Платежи по кредиту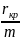: Qкр , Qкр ,…,Qкр + Qкр

Затем нужно сложить оба потока платежей по портфелю(по кредиту и свопу) и сравнить дюрации по портфелю и просто кредиту.

Dэф (портфеля) < Dэф (кредита). В этом состоит хеджирование