
- •1. Дюрация и выпуклость финансовых инструментов с фиксированными доходами
- •2. Эффективная граница множества инвестиционных возможностей при заданном наборе рискованных активов
- •3. Эффективная граница множества инвестиционных возможностей при наличии безрискового актива.
- •4. Модель оценки капитальных активов (capm).
- •5. Форвардные контракты. Форвардная цена активов и ее оценка
- •6. Фьючерсные контракты. Хеджирование с помощью фьючерсов
- •7. Процентные свопы и их оценка
- •Оценка стоимости свопового контракта:
- •8. Валютный своп и его оценка
- •Опционы и их основные характеристики. Паритет цен европейских опционов.
- •Модель Блэка-Шоулса для оценки европейских опционов
- •11. Дельта и гамма хеджирование опционных позиций.
- •12. Модель Мертона для оценки корпоративных ценных бумаг.
- •Модель Ваcичека
- •Модель Халла-Вайта.
- •15. Барьерные опционы и их оценка
- •16. Использование бар. Опционов для оценки корп. Обл.
- •18. Дельта-гамма нормальный метод для оценки рисковой стоимости активов.
- •19. Оценка рыночных рисков на основе обобщенного распределения Фреше.
- •Кредитные потери при дефолтах и их основные составляющие.
- •21. Оценка вероятностей дефолтов на основе рынка корпоративных облигаций
- •Оценка вероятности дефолтов на основе рынка корпоративных облигаций с нулевым купоном.
- •Оценка вероятностей дефолта по рынку купонных облигаций.
- •Модель Мертона для оценки показателей кредитного риска.
- •22. Текущая и потенциальная подверженность кредитному риску
- •1. Оценка текущей подверженности кредитному риску
- •2. Оценка потенциальной подверженности кредитному риску
- •24. Расстояние до дефолтов и ожидаемая частота дефолтов в модели kmv-корпорации
- •26.Основные виды производных кредитных инструментов.
- •Корзинные кредитные свопы (bds)
- •Свопы полного дохода ( Total return swaps –trs)
- •4.Форвардные и опционные контракты на кредитные спреды:
- •5.Кредитные ноты (cln)
- •6.Облигации, обеспеченные долговыми обязательствами.
- •27. Кредитные дефолтные свопы и их оценка
- •28. Триномиальная модель краткосрочной безрисковой процентной ставки
- •29. Операционный риск
- •4.3.2. Альтернативный стандартизованный метод
- •4.4. Усовершенствованные методы измерения
7. Процентные свопы и их оценка
Своп – договор об обмене потоками платежей по некоторой заранее установленной схеме .
В процентном свопе предусмотрен обмен процентных платежей от некоторой суммы А, рассматриваемый по фиксированной процентной ставке r, на процентный платеж от некоторой суммы q, рассматриваемый по плавающей процентной ставке r(m) + ∆.
r(m) – рыночная процентная ставка
Рассмотрим компании А и В на рынке ссудного капитала:
Рассмотрим в виде таблицы процентные ставки, по которым компаниям предлагается кредит:
Таблица 1
-
Компания
Фиксированная ставка
Плавающая ставка
А
rфA(m)
ρ(m) +∆А
В
rфВ(m)
ρ(m) +∆B
Будем считать, что:
rфA(m) < rфВ(m) и ∆А < ∆B (т.е. у компании А абсолютное преимущество на обоих рынках)
(например, кредитный рейтинг А выше В)
rфВ(m) - rфA(m) > ∆B - ∆А ( таким образом, у компании А есть относительное преимущество на рынке ссудного капитала с фиксированной процентной ставкой, а у компании В – относительное преимущество на рынке ссудного капитала с плавающей процентной ставкой)
Предположим, что компании А необходим кредит с плавающей процентной савкой величиной Q, а компании В необходим кредит с фиксированной процентной ставкой.
Если компании необходимы долгосрочные инвестиции, то она предпочтет кредит с фиксированной процентной ставкой, т.к. так можно оценить предстоящие расходы. Кредит с плавающей процентной ставкой предпочтительнее при финансировании оборотного капитала.
х

rфA(m)
Если δ1+δ2 = (rфB(m)-rфA(m)) – (∆В - ∆А), то компании могут получить интересующие их кредиты и также получить процентный выигрыш δ1 (для А) и δ2 (для В).В
ρ(m)
Q
Q
ρ(m) +∆B
А


Таким образом, компании берут кредиты там, где у них есть преимущество.
Компании могут договориться об обмене процентными платежами, чтобы обеспечить обозначенный выше процентный выигрыш.
Компания В платит х + ∆B , а для чистого выигрыша должно быть: х + ∆B = rфВ(m) – δ2
rфВ(m) – платила бы компания В, если бы не заключила договор с А
Следовательно, х = rфВ(m) – ∆B - δ2
Компания А также получит выигрыш:
Чистый платеж А: ρ(m) + rфA(m) – х = ρ(m) + rфA(m) - rфВ(m) + ∆В + δ2 (1)
δ1+δ2 = (rфB(m)-rфA(m)) – (∆В - ∆А), тогда
= ρ(m) + ∆А - ∆В - δ1 - δ2 + ∆В + δ2 = ρ(m) + ∆А - δ1,
В случае, если бы между компаниями не был заключен договор, А платила бы: ρ(m) + ∆А , таким образом, выигрыш есть.
Препятствия:
Компаниям трудно найти друг друга для заключения такого контракта
Перед заключением свопового контракта (который, как правило, является долгосрочным), компании должны проанализировать финансовое состояние друг друга.
Д
rАф
y
x
ля устранения этих препятствий компании часто прибегают к помощи посредника, который будет заниматься организацией сделок. Чаще всего это банк, который получает маржу μ. В этом случае и компания А получает выигрыш δ1, и компания В получает выигрыш δ2.


А

В
Банк

ρ(m) + ∆B
ρ(m)
ρ(m)
х = rфВ(m) – ∆B - δ2,
y = rфA(m) – ∆A + δ1,
В реальных условиях банк диктует свои условия, задавая маржу μ . Им составляется таблица котировок:
Таблица 2
-
Число периодов
Фиксированная ставка, которую банк готов получать в обмен на рыночную ставку ρ(m)
Фиксированная ставка, которую банк готов платить в обмен на рыночную ставку ρ(m)
1
r(1)(1)
r(2)(1)
2
r(1)(2)
r(2)(2)
…
….
….
l
r(1)(l)
r(2)(l)
…
…
…
N
r(1)(N)
r(2)(N)
Заметим,
что r(1)(1)
= r(2)(1)
= ρ0(m)
(нет неопределенности), μ
=
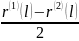 – маржа банка при
процентных свопах на l
– периодов. Тогда rсв(l
) =
– маржа банка при
процентных свопах на l
– периодов. Тогда rсв(l
) =
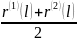 – процентная ставка, которую финансовый
институт готов получать или платить в
обмен на рыночную процентную ставку,
если он не берет маржу. Эту ставку
называют своповой
процентной ставкой на l
– периодов.
– процентная ставка, которую финансовый
институт готов получать или платить в
обмен на рыночную процентную ставку,
если он не берет маржу. Эту ставку
называют своповой
процентной ставкой на l
– периодов.
В момент заключения свопового контракта его ставка равна 0 (без учета маржи), в течение времени его стоимость может меняться для обоих сторон, т.к. ρ(m) известна.
