6. Фьючерсные контракты. Хеджирование с помощью фьючерсов

Фьючерсным контрактами или просто фьючерсами называют форвардные контракты, торговля которыми производится на специальных биржах.

Чтобы исключить или по, крайней мере, уменьшить рискованность позиции инвестора по исходным активам, используется хеджирование.

Короткий хедж. Если инвестор на временном промежутке занимает короткую позицию по исходным активам и существует фьючерсный контракт на эти активы с датой поставки t, то в мом он может открыть короткую позицию по этому фьючерсному контракту. Тогда в мом t инвестор сможет продать активы по заранее установленной цене.

Длинный хедж. Аналогично, только инвестор занимает длинную позицию.

Пусть инвестор на промежутке занимает определенную позицию исходным активам и для хеджирования ед исходных активов решает использовать фьючерсный контракт на ед каких-то других активов с датой поставки T (T>t).

Тогда чистый доход 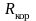( 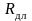) от одной хеджируемой позиции по исходным активам можно найти следующим образом.

=

=

где и - фьючерсные цены хеджируемых активов

- спот цена активов в мом t и соответственно.

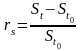Если - доходность одной хеджируемой позиции при короткой позиции по исходным активам, то где - доходность хеджируемых активов

-доходность фьючерсной позиции.

Аналогично

Показатель хеджирования – это отношение количества хеджируемых позиций к объему всех позиций инвестора по исходным активам . Если выбран показатель хеджирования k,

где Q- обьем позиции инвестора по исходным активам

А- оббьем одного фьючерсного контракта, используемого для хеджирования.

Пусть инвестор на промежутке занимает короткую позицию по исходным активам и при выборе стратегии хеджирования минимизирует дисперсию доходности.

Если - доходность совокупной позиции инвестора при показатели хеджирования k, то =

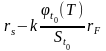
Тогда дисперсия доходности совокупной позиции инвестора определяется равенством

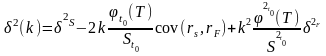
и - дисперсия доходности исходных активов и одной фьючерсной позиции соответственно.

Вывод. Дисперсия будет наименьшей

Следствие. Чтобы уменьшить риск стратегии хеджирования, хеджируемые активы следует выбирать так, чтобы коэффициент корреляции между доходностью хеджируемых активов и доходностью фьючерсной позиции по хеджирующим активам была наибольшей.

Хеджирование портфелей акций с помощью фьючерсных контрактов на индекс акции.

По условию форвардного контракта сторона, занявшая в мом короткую позицию, в мом исполнения контракта Т получит денежную сумму в размере

где -значения индекса акции на мом Т

- фьючерсная цена индекса акции а мом

L-обьем контракта

Фьючерсный контракт на активы можно рассматривать как форвардный контракт на активы с постоянной дивидендной доходностью

(1) где q-постоянная дивидендная доходность индекса акций

Пусть инвестор владеет некоторым портфелем акций, стоимость которого в мом равна Р( ), инвестор решает хеджировать свою позицию с помощью фьючерсных контрактов на индекс акций и занимает короткую позицию в N таких контрактов.

Доходность от совокупной хеджируемой позиции составит

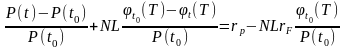
Наименьшее значение дисперсии хеджируемой позиции

Достигается при N=

Из (1) получаем

Вместе с тем где -доходность индекса акций за время

Тогда

величина обычно достаточно мала и можно считать =1

Вывод где - бета-коэффициент исходного портфеля акций относительно рассматриваемого индекса акций.

Хеджирование процентного риска с помощью фьючерсных контрактов.

Рассмотрим фьючерсный контракт на облигацию без дефолт-риска, по которой в моменты

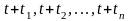должны выплачиваться суммы соответственно. Дата исполнения фьючерсного контракта-Т.

Фьючерсный контракт на облигацию можно рассматривать как форвардный контракт на активы с известными доходами. Тогда фьючерсная цена облигации в текущий мом t

где -цена исходной облигации а текущий мом t

-приведенная стоимость платежей, поступающих от облигации за время от t до T.

Если в текущий мом t все без проц ставки одинаковы и равны , то

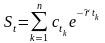и

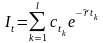
Следовательно

Тогда

где 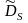-дюрация потока платежей по облигации, поступающих после даты исполнения фьючерсного контракта.

Таким образом, если сразу же после текущего мом t все безрисковые проц ставки изменить на одну и ту же величину , то

Замечание1.

Если исходная облигация является чисто дисконтной, то

,

Заменчание2.

Если исходная облигация является купонной, а срок до ее погашения намного больше срока исполнения фьючерсного контракта, то

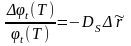
Теорема. Кокса-Ингеррсолла-Росса.

Фьючерсная цена активов всегда совпадает со стоимостью требования на получение в конце дня (t+n) выигрыша в размере

, где -спот цена активов на конец дня (t+n)

-Годовая безрисковая процентная ставка на один день при непрерывном начисление, наблюдаемая в конце дня (t+i).