4. Модель оценки капитальных активов (capm).

Рассмотрим финансовый рынок, на котором обращаются рискованные активы n видов и оперируют n инвесторов.

Будем считать, что инвесторы имеют однородные ожидания относительно рассматриваемого финансового рынка и могут неограниченно предоставлять кредиты и брать ссуды под безрисковую ставку

Теорема. Предположим, что все инвесторы являются несклонными к риску. Если совершенный или почти совершенный рынок находится в равновесии, то

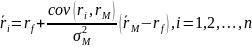
где 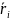- ожидаемая доходность активов i-ого вида;

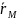- ожидаемая доходность рыночного портфеля;

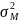- дисперсия доходности рыночного порфеля;

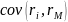- ковариация между доходностью активов i-ого вида и доходностью рыночного портфеля.

Замечание. Число

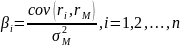
Является бета-коэффициентом рискованных активов i-ого вида.

Система соотношений

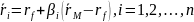
Однако вывести данное соотношение можно и без предположения о том, что все инвесторы являются несклонными к риску. Для этого необходимо следующая лемма:

Лемма. Если функция полезности 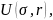где , ,

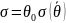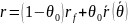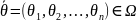, а 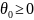, достигает своего наибольшего значения при 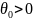, то в точке глобального максимума этой функции отношение

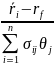
Принимает одно и то же значение для всех

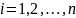
В таком случае модель оценки финансовых активов можно сформулировать в следующем виде:

Теорема. Если совершенный рынок финансовых активов находится в равновесии, то

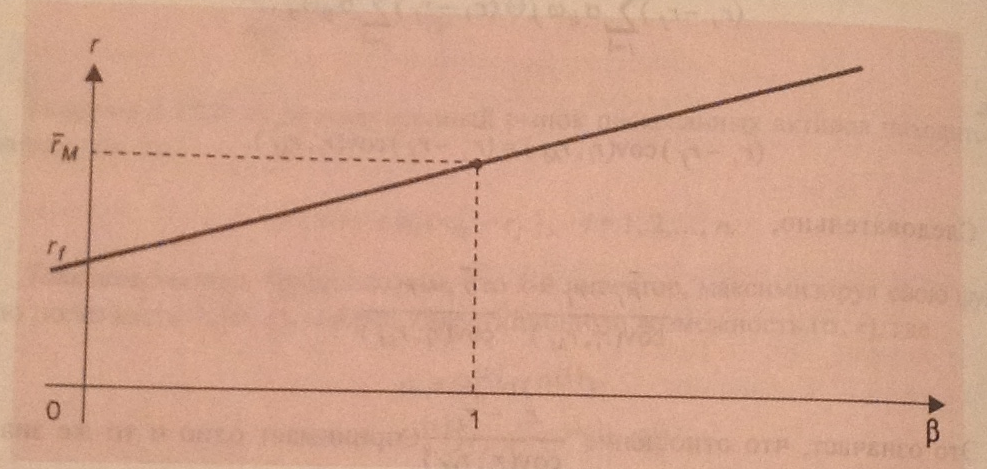
Определение. Линией рынка рискованных активов называется прямая, задаваемая уравнением:

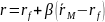
Линия рынка рискованных активов изображает зависимость равновесной ожидаемой доходности рискованного актива от бета-коэффициента этого актива.

5. Форвардные контракты. Форвардная цена активов и ее оценка

Форвардный контракт представляет собой соглашение купить (продать) некоторые активы в определенный момент в будущем по заранее установленной цене.

Определение. Цена поставки, по которой в текущий момент t заключаются форвардные контракты на активы данного вида с датой исполнения T, называется форвардной ценой активов на срок (T-t) лет и обозначается через .

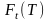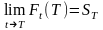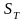Цена актива должна удовлетворять условию: где - спот-цена активов на момент исполнения форвардного контракта.

Замечание. Можно считать, что

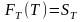
Теорема. Предположим, что существует безрисковая процентная ставка 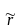срок Т-t лет при непрерывном начисление. Тогда текущие стоимости длинной и короткой позиции в мом t можно ценить следующим образом

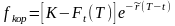
Доказательство. В мом t, уплатив сумму , можно получить длинную позицию в форвардном контракте на единицу исходных активов с ценой поставки К. Одновременно можно занять короткую позицию в форвардном контракте на ед этих же самых активов с ценой поставки .

Тогда, купив в мом исполнения контракта Т активы по цене К, можно продать их по цене . Значит в мом времени Т без какого-либо риска будет получен доход в размере -К. При отсутствие прибыльных арбитражных возможностей доходность данной инвестиции должна совпадать с безрисковой процентной ставкой , т.е.

↕

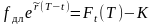
Форвардные цены активов и их оценка.

1. Форвардные цены чисто дисконтных облигаций без дефолт-риска.

Пусть в текущий мом t на рынке имеется чисто дисконтная облигация без дефолт риска номинала А, датой погашения 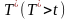. Обозначим через текущую форвардную цену рассматриваемой облигации на срок (T-t) лет.

Покажем, что при отсутствие прибыльных арбитражных возможностей должно выполняться следующие равенство

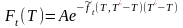
где 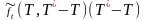- предполагаемая форвардная процентная ставка при непрерывном начисление на будущий период от T до 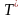лет, наблюдаемый в мом t.

Док-во. Рассмотрим следующую стратегию в текущий мом t купим чисто дисконтную облигацию по цене 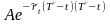и одновременно займем короткую позицию в форвардном контракте на эту облигацию с датой поставки Т.

Продав имеющуюся у нас облигацию по условиям форвардного контракта, мы без какого-либо риска получим в мом Т доход в размере .

Из предположения об отсутствие прибыльных арбитражных возможностей следует, что доходность данной инвестиции, начальные затраты на которую составляют , должна совпадать с безрисковой процентной ставкой 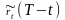. Это означает, что должно выполняться следующие равенство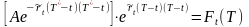

т.е.

2. Форвардная цена активов при известной приведенной стоимости доходов.

Форвардная цена активов при известной приведенной стоимости доходов от этих активов должна удовлетворять равенству

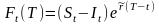
где 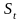- спот цена активов в текущий мом t

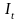- приведенная стоимость доходов, поступающих от активов за время от t до T

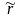- безрисковая процентная ставка на срок (T-t) лет при непрерывном начисление.

Док-во. Если 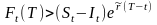, то возможна следующая прибыльная арбитражная стратегия занять короткую позицию в форвардном контракте и, взяв сумму в кредит на срок (T-t) лет под безрисковую процентную ставку , купить эти активы. В мом исполнения контракта Т будет получен безрисковый доход, так как

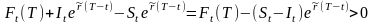
Если же 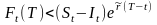, то производится короткая продажа, а полученные средства инвестируются на срок (T-t) лет и занимается длинная позиция в форвардном контракте на эти активы. Тогда доход на мом Т составит

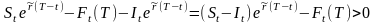
3. Форвардная цена активов с постоянной непрерывной дивидендной доходностью.

Предположим, что все доходы, поступающих от активов, инвестируются в эти активы. Если при этом за любое время каждая единица активов превращается в 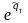единиц, то говорят, что активы обладают постоянной дивидендной доходностью 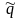при непрерывном начисление.

Иностранную валюту можно рассматривать как актив с постоянной дивидендной доходностью. В самом деле, единицу иностранной валюты можно инвестировать под безрисковую процентную ставку 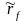в той стране, где действует эта валюта. Тогда через лет единица этой валюты превратится в 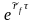единиц. Таким образом, иностранная валюта обладает постоянной дивидендной доходностью и она совпадает с безрисковой процентной ставкой .

Во многих случаях рыночные индексы акций можно рассматривать как активы с постоянной дивидендной доходностью.

Форвардная цена активов с постоянной дивидендной доходностью может быть записана следующим образом 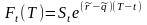,где Т- дата поставки активов.

Действительно, можно построить следующую безрисковую стратегию в мом t купить 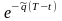единиц активов и занять короткую позицию в форвардном контракте на единицу этих активов.

В мом поставки Т мы будем обладать единицей активов, тк 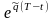=1, которую продадим за , согласно короткой позиции в форвардном контракте. Начальные затраты составляют 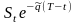, а доходность ее должна совпадать с безрисковой процентной ставкой . Следовательно

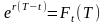
Тогда стоимости длинной и короткой позиции в форвардном контракте на активы с постоянной дивидендной доходностью можно определить как

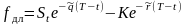
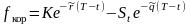
Форвардные цены товаров.

Пусть - форвардная цена единицы некоторого товара в текущий мом t, дата поставки которого Т.

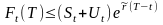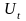Тогда , где - приведенная стоимость на хранение единицы товара за время (T-t) лет