28. Триномиальная модель краткосрочной безрисковой процентной ставки

и ее использование

Модель Халла-Уайта учитывает эффект возвращения к среднему, что не учитывается в биномиальной модели процентной ставки. Следовательно, для моделирования СП Халла-Уайта необходимо предложить альтернативную модель. Такой моделью является триномиальная модель краткосрочной безрисковой процентной ставки (далее – КБПС). Предположим, что КБПС определяется моделью Халла-Уайта: . Для построения триномиальной модели сначала выбирается число h>0. Пусть - безрисковая ПС при непрерывном начислении на h лет, наблюдаемая в момент . Если h невелико, то можно предположить, что удовлетворяет тому же стохастическому дифференциальному уравнению, что и КБПС: при начальном условии R(0)=R₀. Построение модели осуществляется в 2 этапа.

Этап 1

Модель строится для СП Заметим следующее: . Зная, что приращения винеровского СП обладают нулевым мат. ожиданием и дисперсией 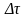, можем оценить мат. ожидание и дисперсию приращения : .

При : . Рассмотрим моменты времени 0,h,2h,…,ih,… В каждый момент ih ставка может принимать значения , где . Если в момент ih ставка приняла значение , соответствующий узел будем обозначать (i,j). Из узла (i,j) возможен переход в один из трех узлов: (i+1,j₁), (i+1,j₂) или (i+1,j₃). Такой процесс называется ветвлением. В триномиальной модели используется три вида ветвлений:

1. Стандартное ветвление: . Таким образом, изменение процентной ставки возможно на величины , 0 и с вероятностями p_u, p_m и p_d соответственно. Вероятности можно найти, решая следующую систему:

С учетом того, что , система приводится к виду . Разрешая систему, получим формулы для вероятностей переходов: , , . Чтобы вероятности были положительными, использование стандартного ветвления возможно только в узлах, где выполняется ограничение: .

2. Ветвление 1-го вида: 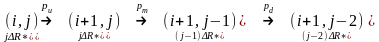. Расписывая систему аналогично предыдущему случаю, получим следующие выражения для вероятностей: , , . Чтобы вероятности были положительными, ветвление используется при ограничении .

3. Ветвление 2-го вида: . Выражения для вероятностей: , , . Чтобы вероятности были положительными, ветвление используется при ограничении .

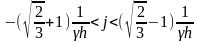Таким образом, чтобы определить тип ветвления, который необходимо использовать в том или ином узле, необходимо рассчитать . Если 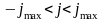, то используется стандартное ветвление. При больших j – ветвление 1-го вида, при меньших – второго вида.

Этап 2

Чтобы построить триномиальную модель не для процесса R*, а для R, нужно заметить следующее: . Это обыкновенное дифференциальное уравнение. Пусть . Тогда имеем уравнение 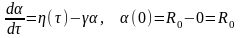. Это линейное дифф. уравнение. Его можно разрешить. Таким образом, построение триномиальной модели для R сводится к следующему:

1. Построение модели для СП R*:

2. Решение обыкновенного д.у., приведенного выше – получение функции .

3. Прибавление ко всем ставкам триномиальной модели на i-м этапе числа .

Если известна временная структура процентных ставок, то функцию можно подобрать так, чтобы рыночная временная структура совпадала с теоретической.

Триномиальная модель используется для оценки инструментов, производных от КБПС. Например, ее можно использовать для оценки американских опционов, кепов, флоров, колларов, облигаций со встроенными опционами и других инструментов, производных от КБПС, чего не позволяют делать напрямую формулы модели Халла-Уайта (только ч.д. облигации, купонные обл. и евр. опционы на облигации).