6.Облигации, обеспеченные долговыми обязательствами.

Рассмотрим большой портфель корпоративных облигаций (или банковских кредитов). Пусть номинал всех облигаций одинаков, а номинал всего портфеля А. На основании портфеля формируется 4 транша новых ц.б. Основная сумма 1-го транша может составлять 5% от номинала всего портфеля, она уменьшается пропорционально кредитным потерям по всему портфелю. Если кредитные потери по портфелю достигнут 0.05А, то основная сумма 1ого транша окажется нулевой и 1 транш будет полностью исчерпан.(т.е. 1ый транш поглощает первые 5% кр. потерь (СL) по портфелю).

Если CL составят 0,01А, то основная сумма 1ого транша уменьшится на 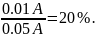Если CL=0.025A, то на 50%. При обеспечении таким потоком выпускается новая облигация с купонной ставкой f ≈35%. Основная сумма облигации и % по ней снижаются, при достижении кр. потерями 0.05A держатели облигации ничего не получат. Высокая купонная ставка, транш очень рискованный.

Основная сумма 2ого транша может быть 10% от А. ( вторые 10% CL по портфелю) и она не меняется, пока CL не достигнут 5% от A. При CL=0.07A, основная сумма второго транша снизится на 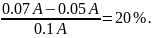При достижении CL 15% от A транш исчерпывается. (2ой транш менее рискованный, чем 1ый). По облигациям из этого транша обычно выплачиваются % по ставке LIBOR+ .

Основная сумма 3его транша - 10%. (следующие 10% СL).Осн. сумма уменьшается аналогично. Транш исчерпан при достижении СL 25% от А. По 3ему траншу выплачиваются % по ставке LIBOR+ .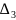

Основная сумма 4ого транша вначале составляет 75% от А и он поглощает все остальные CL по портфелю. По нему выплачиваются проценты по ставке LIBOR+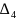 , где 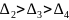. Практически безрисковый, часто не продается.

Идея:

Способ из низкосортных кредитов сделать высококачественный продукт (секьюритизация кредитного рынка). Кроме того, продавая облигации, соответствующий фонд получит средства, которые можно использовать для новых кредитов (это может привести к тяжелым последствиям, так как надежность заемщиков будет снижаться с ростом объема выданных кредитов).

В настоящее время строятся синтетические облигации, обеспеченные долговыми обязательствами.

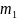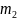Рассм. портфель с одинаковыми номиналами. Рассм. корзинный кредитный своп от 0-ого до -ого дефолта. Такой своп надо продать, тогда покупатель будет иметь платежи, аналогичные 1ому траншу. Аналогично корз. своп от -ого до -ого дефолта -2ой транш….

27. Кредитные дефолтные свопы и их оценка

Стандартный кредитный своп формируется на основе облигации, выпущенной некоторой компанией С (ее называют определяющей компанией, а облигацию – определяющей облигацией). Инвестор А занимает длинную позицию в кредитном свопе, выпущенном компанией В, если инвестор А периодически выплачивает компании В проценты по фикс. процентной ставке от условной основной суммы Q вплоть до дефолта определяющей компании С или до окончания срока действия свопа. Взамен А получает право продать определяющую облигацию номиналом Q в случае дефолта определяющей компании за ее номинальную стоимость (фактическая продажа как правило не происходит, вместо этого А получает сумму Q-Q_рын, где Q_рын – рыночная стоимость облигации вскоре после дефолта компании С).

Фиксированную ставку, выплачиваемую стороной с длинной позицией называют спредом кредитного свопа. Таким образом, компания В (покупатель риска или продавец защиты) получает периодические платежи, а инвестор А (продавец риска или покупатель защиты) получает дефолтный платеж при дефолте определяющей компании.

Покупка некоторой корпоративной облигации с купонной ставкой f+w эквивалентна портфелю:

1. покупка облигации без риска дефолта со ставкой f с теми же характеристиками, что и корпоративная;

2. короткая позиция в кредитном свопе со спредом w с определяющей корп. облигацией.

Действительно, пусть купоны оплачиваются 2 раза в год. Рассмотрим поток платежей, получаемых инвестором. Если дефолт определяющей компании не происходит, то в случае покупки корпоративной облигации он получит сумму (f+w)Q каждые полгода. Поток платежей от портфеля аналогичный (fQ за счет безрисковой облигации, wQ за счет свопа). Если же дефолт происходит, то в момент дефолта инвестор может продать безрисковую облигацию, и в итоге, совершив дефолтный платеж, получит от портфеля 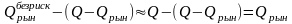(т.к. стоимость безрисковой облигации близка к номиналу). Аналогичную сумму получит держатель корпоративной облигации, если продаст ее вскоре после дефолта.

Существует разновидность кред. свопов – бинарные кредитные свопы. Они отличаются от стандартных тем, что в случае дефолта определяющей компании сторона с длинной позицией получает фиксированную денежную сумму.

Для оценки кредитных свопов необходимо знать, как оценивать спред. Рассмотрим своп, в котором определяющей является облигация с купонами, выплачиваемыми m раз в год. Условная денежная сумма Q, дата окончания свопа T, спред s. Предположим, что дефолт определяющей компании может наступить только в фикс. моменты 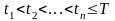. При этом предполагаются известными вероятности дефолта определяющей компании в мире, нейтральном к риску, в эти моменты: p₁,…,p_n. Пусть - время от момента t=0 до первого купонного платежа и 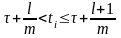. 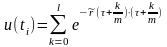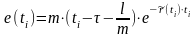Введем обозначения: , , где 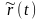- безрисковая ставка при непрерывном начислении на срок t лет. Тогда приведенная стоимость потока платежей, выплачиваемого стороной с длинной позицией, до момента t_i, имеет вид: 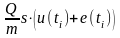. Ожидаемая приведенная стоимость выплачиваемого стороной потока: 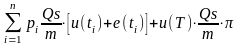, где . Ожидаемая приведенная стоимость потока платежей, получаемого стороной с длинной позицией: 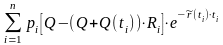, где R_i - ставка восстановления долгов в момент t_i. Q(t_i) – накопленные проценты к моменту t_i. Справедливый кредитный спред находится из условия равенства приведенных ожидаемых стоимостей двух потоков: выплачиваемого и получаемого стороной с длинной позицией. Приравнивая приведенные выше выражения, можно выразить: 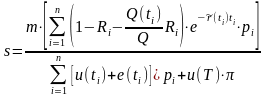. В случае бинарного кредитного свопа поток, выплачиваемый стороной с дл. позицией не изменится, а ожидаемая приведенная стоимость получаемого потока составит 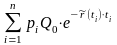, где Q₀ – фиксированная сумма, получаемая при дефолте определяющей компании. Тогда спред бинарного свопа определяется формулой: 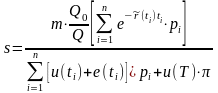. Основное ограничение модели: дефолты могут происходить лишь в определенные моменты времени.

Рассмотрим модель, в которой дефолт может произойти в любой момент. Предполагается известной плотность вероятностей дефолта q(t). Пусть u(t) – приведенная стоимость купонного платежа в размере 1 д.е. за время от 0 до t, e(t) – приведенная стоимость платежа в размере m(t-t*), выполненного в момент t, где t* - ближайший предшествующий момент оплаты купона. R(t) – ставка восстановления долгов в момент t. Q(t) – накопленные проценты к моменту t. Тогда по аналогии с предыдущим случаем, используя для определения ожидаемой стоимости потоков интегрирование вместо суммирования, получим: .

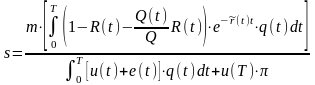В настоящее время рынок кредитных свопов достаточно ликвидный, присутствует много различных свопов. Следовательно, на основе рыночной информации о спредах можно найти предполагаемые вероятности дефолта компаний. Пусть свопы с одной определяющей компанией со сроками t₁,…,t_n имеют спреды s₁,…,s_n. Плотность вероятностей дефолта компании между моментами t_k-1 и t_k постоянна и равна q_k. Платежи стороны с дл. позицией в каждом свопе в производятся m раз в год, ставка восст. долгов в момент t равна R(t). Введем обозначения: ; ; .

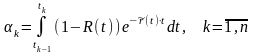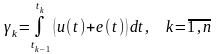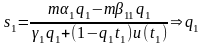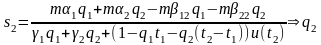Тогда, зная выражение для спреда s₁, можем выразить q₁: . Затем, зная выражение для s₂ и значение q₁, можем выразить q₂: . Продолжая данную рекурсивную процедуру, можно найти значения плотности на остальных промежутках.