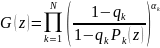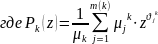- •1. Дюрация и выпуклость финансовых инструментов с фиксированными доходами
- •2. Эффективная граница множества инвестиционных возможностей при заданном наборе рискованных активов
- •3. Эффективная граница множества инвестиционных возможностей при наличии безрискового актива.
- •4. Модель оценки капитальных активов (capm).
- •5. Форвардные контракты. Форвардная цена активов и ее оценка
- •6. Фьючерсные контракты. Хеджирование с помощью фьючерсов
- •7. Процентные свопы и их оценка
- •Оценка стоимости свопового контракта:
- •8. Валютный своп и его оценка
- •Опционы и их основные характеристики. Паритет цен европейских опционов.
- •Модель Блэка-Шоулса для оценки европейских опционов
- •11. Дельта и гамма хеджирование опционных позиций.
- •12. Модель Мертона для оценки корпоративных ценных бумаг.
- •Модель Ваcичека
- •Модель Халла-Вайта.
- •15. Барьерные опционы и их оценка
- •16. Использование бар. Опционов для оценки корп. Обл.
- •18. Дельта-гамма нормальный метод для оценки рисковой стоимости активов.
- •19. Оценка рыночных рисков на основе обобщенного распределения Фреше.
- •Кредитные потери при дефолтах и их основные составляющие.
- •21. Оценка вероятностей дефолтов на основе рынка корпоративных облигаций
- •Оценка вероятности дефолтов на основе рынка корпоративных облигаций с нулевым купоном.
- •Оценка вероятностей дефолта по рынку купонных облигаций.
- •Модель Мертона для оценки показателей кредитного риска.
- •22. Текущая и потенциальная подверженность кредитному риску
- •1. Оценка текущей подверженности кредитному риску
- •2. Оценка потенциальной подверженности кредитному риску
- •24. Расстояние до дефолтов и ожидаемая частота дефолтов в модели kmv-корпорации
- •26.Основные виды производных кредитных инструментов.
- •Корзинные кредитные свопы (bds)
- •Свопы полного дохода ( Total return swaps –trs)
- •4.Форвардные и опционные контракты на кредитные спреды:
- •5.Кредитные ноты (cln)
- •6.Облигации, обеспеченные долговыми обязательствами.
- •27. Кредитные дефолтные свопы и их оценка
- •28. Триномиальная модель краткосрочной безрисковой процентной ставки
- •29. Операционный риск
- •4.3.2. Альтернативный стандартизованный метод
- •4.4. Усовершенствованные методы измерения
24. Расстояние до дефолтов и ожидаемая частота дефолтов в модели kmv-корпорации
Предполагается, что структура капитала каждого заемщика имеет следующий вид:
Акция (с дивидендами)
Краткосрочная задолженность
Долгосрочная задолженность
Привилегированная акция
Стоимость акции предполагается равной стоимости опциона «колл», где базовым активом является рыночная стоимость активов фирмы
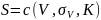
Чтобы оценить стоимость активов фирмы и волатильность стоимости активов используют следующую систему:
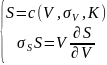
Пороговое значение стоимости активов вычисляется, как сумма краткосрочной задолженности и половина долгосрочной задолженности. DP=STD+0.5LTD
DP – strike price (X – в формуле БШ)
Можно оценит расстояние до дефолта:

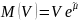
Т.к.
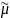 (доходность
активов) найти сложно, то предполагают,
что
(доходность
активов) найти сложно, то предполагают,
что
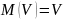
По значениям DD можно группировать клиентов и оценивать частоту дефолтов из каждой группы:
Пусть
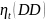 - количество фирм, у которых на начало
года t
расстояние до дефолта составило заданную
величину.
- количество фирм, у которых на начало
года t
расстояние до дефолта составило заданную
величину.
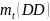 -
количество фирм, у которых на начало
года t
расстояние до дефолта составило заданную
величину, и которые задефолтились к
концу года t.
-
количество фирм, у которых на начало
года t
расстояние до дефолта составило заданную
величину, и которые задефолтились к
концу года t.
Тогда
 – частота дефолтов в году t.
– частота дефолтов в году t.
Ожидаемая частота дефолтов рассчитывается по формуле:
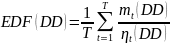
Замечание: EDF – оценка вероятности дефолта (PD) в «реальном мире»
25. Модель Credit-Risk «+» при известных вероятностях дефолтов.
Если
дефолты независимы, а
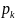 (вероятность def заемщика
A в течение года) мало, то
можно считать, что число дефолтов по
портфелю распределено по ЗР Пуассона
с параметром µ, равным ожидаемому числу
дефолтов.
(вероятность def заемщика
A в течение года) мало, то
можно считать, что число дефолтов по
портфелю распределено по ЗР Пуассона
с параметром µ, равным ожидаемому числу
дефолтов.
Рассм. кредитный портфель со следующими условиями:
Дефолты независимы
Подверженность КР по всем кредитам одинакова и равна
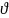
Для всех заемщиков ставка восстановления одинакова и равна R.
Тогда кредитные потери по портфелю записываются в виде
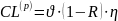
где
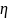 -
число дефолтов в группе
j в
течение года,
-
число дефолтов в группе
j в
течение года,
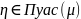 =>
=>
можем построить распределение кредитных потерь и найти все показатели КР для портфеля ( CrVar, определяющийся станд образом). Однако предположение о том, что подверженность по всем кредитам одинакова, нереально.
Одно из преимуществ модели – не требуется никаких рейтингов.
Распределение кредитных потерь по банковскому портфелю при известных вероятностях дефолта.
Рассм. большой банковский кредитный портфель.
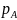 -вероятность
def заемщика A
в течение года.
-вероятность
def заемщика A
в течение года.
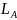 -
подверженность КР со стороны заемщика
A (может быть определена
с учетом ставки восст. R)
-
подверженность КР со стороны заемщика
A (может быть определена
с учетом ставки восст. R)
Ожидаемые
потери по кредиту,
выданному заемщику A: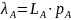
Разобьем заемщиков на группы. Выбирается новая единица измерения L (тыс.р., млн.р.)
Подверженность
кредитному риску в новых единицах:
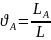 .
Ожидаемые кредитные потери в новых
единицах
.
Ожидаемые кредитные потери в новых
единицах
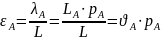 .
Каждую из подверж. риску в новых единицах
увеличиваем до ближайшего целого числа.
Останется отн. небольшое число различных
значений подверженности КР. Заемщиков
с подверженностью
.
Каждую из подверж. риску в новых единицах
увеличиваем до ближайшего целого числа.
Останется отн. небольшое число различных
значений подверженности КР. Заемщиков
с подверженностью
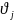 относим в группу j.
относим в группу j.
Рассм.
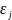 -ожидаемые кредитные
потери по всей группе j.
-ожидаемые кредитные
потери по всей группе j.
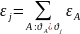
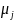 -ожидаемое
число дефолтов в группе j
-ожидаемое
число дефолтов в группе j

Для данного портфеля:
Рассмотрим производящую фукнцию для вероятностей кред. потерь.
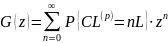
Предположения:
Кредитные потери по группам н/з, =>
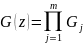 (z)
(z)
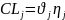 где
где
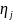 -
число
дефолтов в группе j
в
течение года,
-
число
дефолтов в группе j
в
течение года,
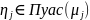
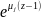 -
ПФВ
для
,
а
-
ПФВ
для
,
а
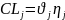 (
-const)
, =>
(
-const)
, =>
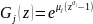
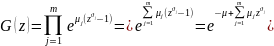 -
ПФВ
для кредитных потерь по портфелю, где
-
ПФВ
для кредитных потерь по портфелю, где
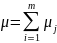 -ожидаемое
число дефолтов по портфелю. Чтобы
получить распределение кредитных
потерь, нужно найти все вероятности
-ожидаемое
число дефолтов по портфелю. Чтобы
получить распределение кредитных
потерь, нужно найти все вероятности
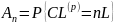 ,
n=0,1,2,..
,
n=0,1,2,..
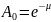
Для
нахождения остальных
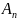 нужно знать производные.(так как по
свойству
нужно знать производные.(так как по
свойству
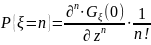 )
)
Проще
ввести рекурсивную формулу для
.
Рассмотрим функцию
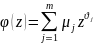
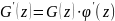
(Используя
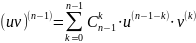 )
)
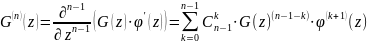
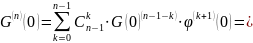
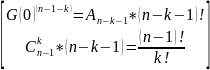
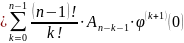
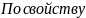
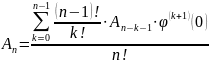 ;
;
 ;
;
Осталось
найти
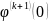
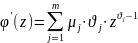
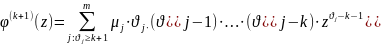
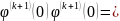
(Так
как
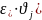 )
)
Тогда
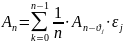
При распределение заемщиков по секторам:
Теорема.
Рассмотрим
кредитный портфель. Пусть заемщики
распределены по N секторам
экономики.
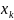 -среднее
число дефолтов в k-ом
секторе. В модели предполагается, что
число дефолтов в k-ом
секторе
-среднее
число дефолтов в k-ом
секторе. В модели предполагается, что
число дефолтов в k-ом
секторе
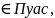 – СВ, имеющая гамма –распределение.
Плотность
– СВ, имеющая гамма –распределение.
Плотность
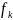 (x) =
(x) =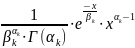 ,
,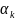 ,
,
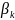 >0
–параметры распределения.
>0
–параметры распределения.
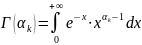
Предполагается,
что дефолты по секторам независимы. (ПФ
для числа дефолтов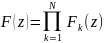 ).
(то есть существует большая зависимость
между дефолтами эмитентов одного
сектора)
).
(то есть существует большая зависимость
между дефолтами эмитентов одного
сектора)
Тогда производящая фукция числа дефолтов по всему портфелю записывается в виде
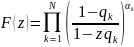 ,
где
,
где
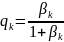 .
.
Для
построения распределения числа дефолтов
надо брать производные F(z),
что трудно. Другой подход основан на
разложении в степенной ряд.
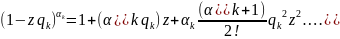
Тогда
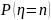 находится как коэффициент при
находится как коэффициент при
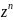 в выражении для
в выражении для
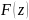 .
.
Как найти коэффициенты , ?
Из
системы
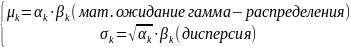 =>
=>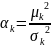 ,
,
Производящая фукция кредитных потерь.
Все заемщики также разбиваются на группы по подверженности КР.
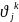 -подверженности
КР
-подверженности
КР
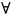 заемщика группы j из k-ого
сектора. (число групп зависит от сектора).
заемщика группы j из k-ого
сектора. (число групп зависит от сектора).
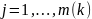
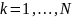
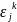 ожидаемые
кредитные потери по всей группе j
из k-ого сектора.
ожидаемые
кредитные потери по всей группе j
из k-ого сектора.
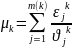 -
ожидаемое число дефолтов в k-ом
секторе.
-
ожидаемое число дефолтов в k-ом
секторе.
Тогда ПФВ кредитных потерь будет иметь вид (опустив док-ва)