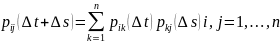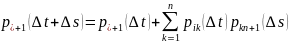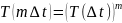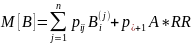1. Оценка текущей подверженности кредитному риску

1) Кредит и облигация. Необходимо оценить рыночную стоимость, подверженную кредитному риску:

- для кредита - считают равной основной сумме долга.

- для облигации – номинальной стоимости облигации

2) гарантии – контракт, по которому банк принимает на себя обязательства третьей стороны (безотзывные)

Пример: банк А выдает кредит компании С, если возврат кредита гарантирует банк В.

Подверженность риску для А и В – основная сумма кредита. Аналогично при выдаче аккредитивов и векселей.

3) Поручительство – контракт, по которому банк берет на себя обязательства по будущей операции, в результате чего он оказывается подвержен кредитному риску.

Пример: банк может обещать минимальную цену облигаций, выпускаемых некоторым эмитентом, если эмитенту не удастся разместить эмиссию на рынке по этой минимальной цене. Поручительства могут быть отзывными

4) Форвардные контракты и свопы. Риск: при положительной стоимости позиции подвержен кредитному риску держатель позиции и наоборот. Стоимость, подверженная кредитному риску может меняться от 0 до… в зависимости от стоимости позиции.

5) Опционы. Кредитный риск только при длинной позиции и равен стоимости опциона.

2. Оценка потенциальной подверженности кредитному риску

- Показателем потенциальной подверженности кредитному риску может служить ожидаемая (математическое ожидание) подверженность кредитному риску.

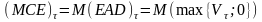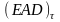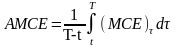- потенциальная подверженность кредитному риску, где - текущая подверженность кредитному риску.

- - средняя подверженность кредитному риску

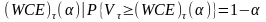- - «наихудшая» подверженность риску на момент τ с уровнем доверия α.

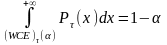
- средняя наихудшая подверженность кредитному риску

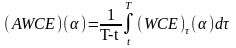
Если известна 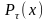- плотность распределения стоимости позиции на момент τ, то 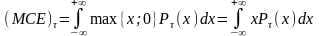, t<=τ<=T

23. CreditMetrics

Матрица рейтинговых миграций и ее свойства

Функционирует кредитно-рейтинговая система из n+1 рейтинга. (1 – самый надежный, n+1 - дефолт).

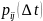- вероятность миграции из рейтинга 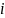в рейтинг 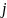за время 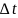. ( – вероятность дефолта из рейтинга за время )

Можно построить матрицу рейтинговых миграций:

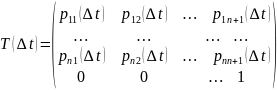
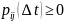
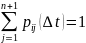
Если клиент/инструмент дефолтится, то он не восстанавливается. При восстановлении заводится новая запись с восстановившимся клиентом. Матрицу можно оценить актуарным методом.

Рассмотрим (i)->(k)->(j)

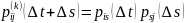(если матрица оценена актуарным методом)

Свойства:

1. 

2. 

3. 

Модель CM в случае одной облигации

1. Дана однолетняя матрица рейтинговых миграций

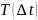
2. Все облигации разнесены по разным категориям кредитного качества (рейтингам).

3. Для каждого рейтинга известны RR и σ(RR) (RR-recovery rate)

4. Для всех облигаций с одной рейтинговой категорией определена ВСПС 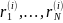. 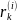- % ставка на K-лет для i-ой рейтинговой категории.

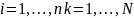
5. Предполагается, что форвардные процентные ставки через год, наблюдаемые от текущего момента времени соответственно равны предполагаемым форвардным процентным ставкам.

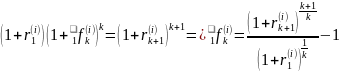
Рассмотрим N-летнюю купонную облигацию. Эмитент находится в i-ой рейтинговой категории. A – номинал облигации.

Если i->j то стоимость облигации 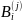рассчитывается по формуле:

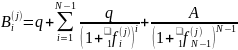
Можно построить распределение стоимости облигации:

Рейтинг эмитента через год	Вероятность	Будущая стоимость облигации через год
1
…	…	…
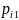
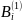
n
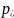
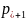
n+1		RR*A

Тогда можно оценить ожидаемую стоимость облигации и стандартное отклонение:

1. 

2. 

Можно оценить рассчитать кредитный VaR и экономический капитал EC с уровнем доверия α

3. 

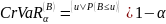
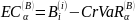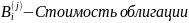4. ( при неизменном рейтинге)

Модель CM в случае портфеля облигации

Нормализованная доходность активов и ее свойства

Предположим, что стоимость активов фирмы задается через СДУ (является процессом геометрического броуновского движения):

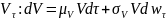
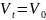
Нормализованная доходность активов фирмы является нормализованным значением решения СДУ:

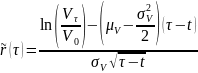
Т.к. 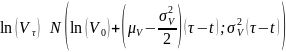, то

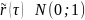
Предположим, что известна матрица рейтинговых миграций:

Рассмотрим -ую строку матрицы рейтинговых миграций и определим критические значения для нормализованной доходности:

…

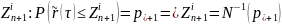
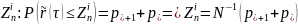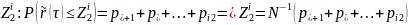
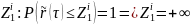
Для моделирования значений нормализованной доходности используем генерацию СВ Монте-Карло. Если значение меньше 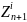, то в данной реализации клиент считается дефолтным. Соответственно, если значение нормализованной доходности попало в интервал (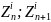 ), то клиент получает худшую недефолтную категорию качества и т.д.

Рассмотрим две фирмы. Рыночная стоимость активов каждой фирмы задается через геометрическое броуновское движение:

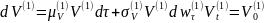
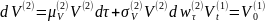
Можно определить корреляционную матрицу между нормализованными доходностями активов двух фирм:

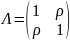
Совместная плотность распределения имеет вид:

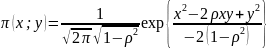
Можно рассчитать совместные вероятности различных миграций

1. (Совместная вероятность дефолта)

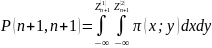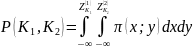2. (Совместная вероятность миграции в произвольные рейтинговые значения)

Примечание: Подобный метод можно использовать для большего значения компаний, коэффициенты корреляций можно оценить по курсам акций разных ОАО.

Алгоритм оценки рисковых показателей портфеля облигаций по методологии CreditMetrics:

1. Моделируются вектор нормализованных доходностей для каждой фирмы

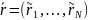
2. Используя преобразование 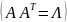учитываем корреляционные связи между фирмами

3. Определяем коридор для нормализованной доходности активов каждой фирмы и определяем рейтинговое значение в данной реализации

4. Используем форвардные % ставки для данного рейтингового значения и оцениваем стоимость каждой облигации в данной реализации.

5. Повторяя шаги (1-4) большое количество раз строим распределение стоимости портфеля облигаций и оцениваем показатели рискованности портфеля: CrVaR, Conditional CrVaR, EC и т.д.