2. Оценка вероятностей дефолта по рынку купонных облигаций.

Пусть на рынке N купонных облигаций, выпущенных эмитентом. Сроки погашения T₁< T₂<…<T_N. Пусть Q_j – стоимость корпоративной облигации, дата погашения которой T_j. Через обозначим стоимость облигации без риска дефолта, аналогичной по всем параметрам корпоративной облигации (j=1…N). Стоимость .

Тогда - приведенная стоимость ожидаемых потерь из-за дефолта.

- вероятность дефолта эмитента в мире нейтральном к риску в момент Т_i, i=1,2..N

- приведенная стоимость потерь по j-й облигации в момент Т_i.

Тогда .

Приведенную стоимость потерь оценивают следующим образом: 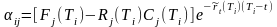, где

- форвардная цена облигации без риска дефолта

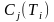- величина требования.

Величину требования можно оценить двумя способами:

1. . Тогда

2. равна номиналу облигации + накопленные проценты.

Тогда имеем систему:

Система из N уравнений с N неизвестными.

Недостаток: можно определить вероятности дефолта лишь в момент погашения корпоративных облигаций.

Плотность вероятности дефолтов – это функция q(τ), если вероятность дефолта за время от t до τ есть .

Приведем стоимость потерь в момент τ по облигации с номером j: 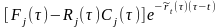. Ожидаемые потеря за время T _i-1 до T_i имеют вид:

. Тогда .

Считая, что T₀=t, а q(τ)= q_i, если T_i>τ>T_i-1, имеем систему линейных уравнений.

3. Модель Мертона для оценки показателей кредитного риска.

Пусть в момент t фирма выпустила 2 ценные бумаги:

1. облигацию номиналом F с датой погашения T с нулевыми купонами

2. обыкновенную акцию, по которой дивиденды не выплачиваются до погашения облигации.

Издержки случае реорганизации фирмы считаются нулевыми.

Тогда стоимость фирмы 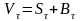, где t<τ<T, - стоимость акции, - стоимость облигации. Оценим стоимость акции и облигации

;

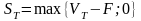; , где и - стоимости опционов «пут» и «колл» соответственно в момент τ.

Стоимость фирмы в любой момент времени τ можно описать стохастическим дифференциальным уравнением: .

Тогда

, где - квази-доля заемных средств в капитале фирмы и ,

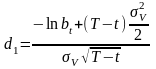
Теперь определим .вероятность дефолта в мире нейтральном к риску.

Как отмечалось, . - ожидаемая непрерывная доходность активов фирмы. В мире нейтральном к риску . Тогда и

. Тогда оценим вероятность дефолта:

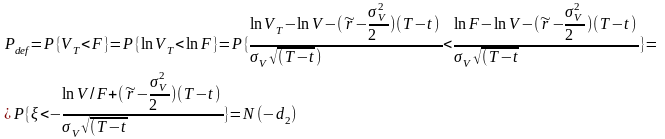
Если в реальном мире мире, то скорее всего . Тогда и, следовательно, , где .

;

, следовательно . Тогда

Если проценты начисляются раз в год, то - на основе CAPM модели. Так как - премия за риск в реальном мире, то

Для производных финансовых инструментов необходимо рассчитывать вероятность дефолта в мире нейтральном к риск, в других случаях – в реальном мире.

Не уверена что нужно включать модель Мертона и сильно ее не описывала (только как в лекции) (хотя, на мой взгляд, надо), спросим на консультации

22. Текущая и потенциальная подверженность кредитному риску

Подверженность кредитному рису при различных финансовых контрактах состоит из двух частей:

- текущей подверженности кредитному риску;

- потенциальной подверженности кредитному риску.