- •1. Дюрация и выпуклость финансовых инструментов с фиксированными доходами
- •2. Эффективная граница множества инвестиционных возможностей при заданном наборе рискованных активов
- •3. Эффективная граница множества инвестиционных возможностей при наличии безрискового актива.
- •4. Модель оценки капитальных активов (capm).
- •5. Форвардные контракты. Форвардная цена активов и ее оценка
- •6. Фьючерсные контракты. Хеджирование с помощью фьючерсов
- •7. Процентные свопы и их оценка
- •Оценка стоимости свопового контракта:
- •8. Валютный своп и его оценка
- •Опционы и их основные характеристики. Паритет цен европейских опционов.
- •Модель Блэка-Шоулса для оценки европейских опционов
- •11. Дельта и гамма хеджирование опционных позиций.
- •12. Модель Мертона для оценки корпоративных ценных бумаг.
- •Модель Ваcичека
- •Модель Халла-Вайта.
- •15. Барьерные опционы и их оценка
- •16. Использование бар. Опционов для оценки корп. Обл.
- •18. Дельта-гамма нормальный метод для оценки рисковой стоимости активов.
- •19. Оценка рыночных рисков на основе обобщенного распределения Фреше.
- •Кредитные потери при дефолтах и их основные составляющие.
- •21. Оценка вероятностей дефолтов на основе рынка корпоративных облигаций
- •Оценка вероятности дефолтов на основе рынка корпоративных облигаций с нулевым купоном.
- •Оценка вероятностей дефолта по рынку купонных облигаций.
- •Модель Мертона для оценки показателей кредитного риска.
- •22. Текущая и потенциальная подверженность кредитному риску
- •1. Оценка текущей подверженности кредитному риску
- •2. Оценка потенциальной подверженности кредитному риску
- •24. Расстояние до дефолтов и ожидаемая частота дефолтов в модели kmv-корпорации
- •26.Основные виды производных кредитных инструментов.
- •Корзинные кредитные свопы (bds)
- •Свопы полного дохода ( Total return swaps –trs)
- •4.Форвардные и опционные контракты на кредитные спреды:
- •5.Кредитные ноты (cln)
- •6.Облигации, обеспеченные долговыми обязательствами.
- •27. Кредитные дефолтные свопы и их оценка
- •28. Триномиальная модель краткосрочной безрисковой процентной ставки
- •29. Операционный риск
- •4.3.2. Альтернативный стандартизованный метод
- •4.4. Усовершенствованные методы измерения
18. Дельта-гамма нормальный метод для оценки рисковой стоимости активов.
Даны некоторые активы, стоимость которых определяется n факторами и моментом времени τ:
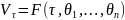
Если F – дважды дифференцируемая функция, то доход за время Δτ:
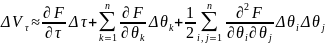
Введем обозначения:
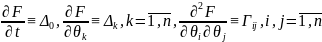
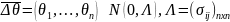
В отличие от дельта-нормального метода, утверждать, что доходность распределена нормально не можем.
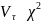
Лемма:
Если
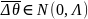 ,
а
– положительно определенная матрица,
то
,
а
– положительно определенная матрица,
то
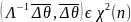 .
.
Доказательство:
Так
как
– симметричная положительная определенная
матрица
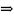 существует ортогональная матрица
существует ортогональная матрица
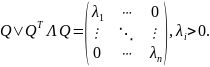
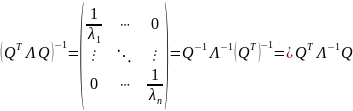
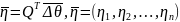
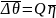
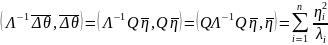
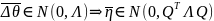
Итак,
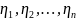 – независимые случайные величины (так
как некоррелированны и распр. нормально),
– независимые случайные величины (так
как некоррелированны и распр. нормально), .
.
 – величина,
распределенная по закону
– величина,
распределенная по закону
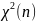 .
.
Теорема:
Доход от актива за время τ оценивается в виде
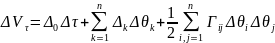
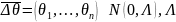 положительно
определена.
положительно
определена.
Если
 где
где
 ,
то
,
то
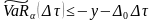 .
.
Доказательство:
Если
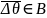 ,
то
,
то
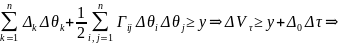
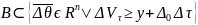 .
.
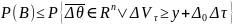
Согласно
одному из свойств рисковой стоимости
активов,
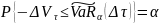 ,
что равносильно
,
что равносильно
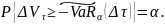
По
определению квантиля
 .
.
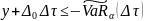
Следствие:
В
условиях теоремы с учетом того, что
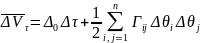 имеем:
имеем:
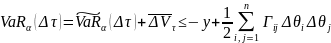
Пример 1:
Пусть текущая стоимость портфеля из облигаций без риска дефолта равняется P. Считается, что кривая рыночных доходностей перемещается параллельно. Величина этого сдвига распределена нормально с нулевым математическим ожиданием и дисперсией .
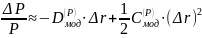
Рассмотрим функцию
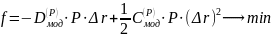
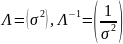
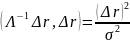
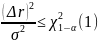
Получаем систему:

Следовательно,
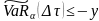 (так как
(так как
 ).
).
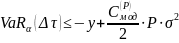 .
.
Пример 2:
Рассматривается купонная облигация с полугодовыми купонами, до погашения которой n полугодовых периодов:
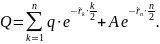
Тогда:
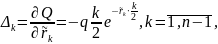
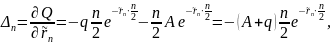
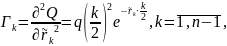
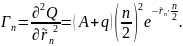
Пример 3:
Оценка рисковой стоимости европейского опциона в модели Блека-Шоулса.
где .
Факторы риска: , . Далее находятся производные I и II порядка c и p по всем факторам риска. Это и будут дельта- и гамма-коэффициенты.
19. Оценка рыночных рисков на основе обобщенного распределения Фреше.
Распределение Фреше (ξ>0):
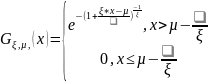
П лотность
распределения Фреше
(при
лотность
распределения Фреше
(при
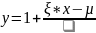 ):
):
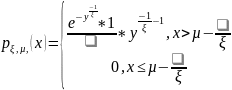
Если СВ η имеет распределение Фреше, то
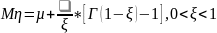
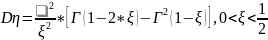
где
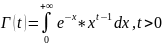
Свойство
обобщенного распределения Фреше: если
0 <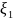 <
<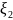 ,
то
,
то
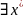 ,
такой что
,
такой что
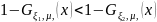 ,
,
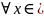 .
Следствие: чем больше ξ,
тем тяжелее правая ветвь распределения.
.
Следствие: чем больше ξ,
тем тяжелее правая ветвь распределения.
Рассмотрим
последовательность однодневных потерь
(независимы и одинаково распределены):
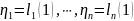 .
.
Пусть
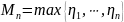
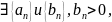 такие
что
такие
что

Найдем
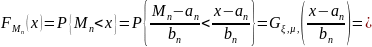
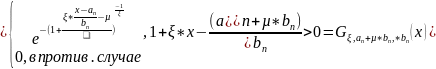
Следовательно,
при достаточно больших n
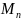 имеет распределение Фреше.
имеет распределение Фреше.
Теорема.
Однодневные экстремальные
потери от активов имеют распределение
Фреше с параметрами ξ, µ,
. β
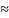 1.
Тогда
1.
Тогда
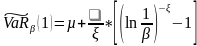 .
.
Доказательство.
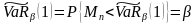
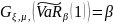
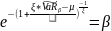
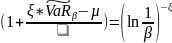
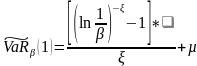
Теорема.
Однодневные экстремальные
потери от активов имеют распределение
Фреше с параметрами ξ, µ,
. β
1.
Тогда
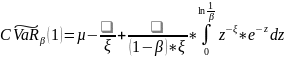 ,
0<ξ<1
,
0<ξ<1
Доказательство.
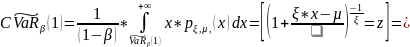
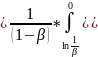


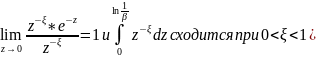
Способы выбора параметра ξ обобщенного распределения Фреше:
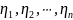 независимы
и одинаково распределены, F(x)
– функция распределения
независимы
и одинаково распределены, F(x)
– функция распределения
Для
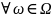 можем упорядочить значения этих величин
по возрастанию:
можем упорядочить значения этих величин
по возрастанию:

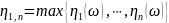
…
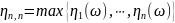
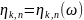 – к-ая
верхняя порядковая статистика
– к-ая
верхняя порядковая статистика
Теорема.
Пусть
независимы и одинаково распределены,
F(x) – функция
распределения. Тогда
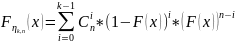 .
.
Теорема.
Пусть
независимы и одинаково распределены.
Если эти СВ имеют распределения Фреше
с параметрами с ξ,
µ, ,
то при
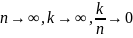 последовательность
последовательность

Следствие.

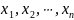 ,
где n достаточно
велико и
,
где n достаточно
велико и
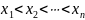
Тогда для оценки параметра ξ можно использовать оценку Хилла:
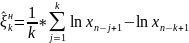
k
выбираем так, чтобы график зависимости
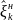 был почти горизонтальный.
был почти горизонтальный.
Из МНК, используя мало измен. функции (
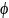 )
)
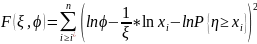
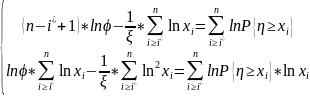
Из
системы находим оценку
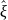 ,
,
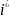 определяем так, чтобы оставался хвост,
равный
определяем так, чтобы оставался хвост,
равный
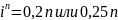
Принцип максимального правдоподобия (самый точный):
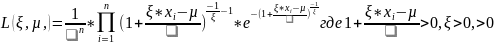
Берем
логарифм этого выражения, ищем точку
глобального минимума на множестве
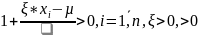
Остальные параметры (µ,) обобщенного распределения Фреше находим из системы: