13. 16. Использование бар. Опционов для оценки корп. Обл.

Оценка куп. облигаций с 0-куп. при наличии барьера.

Пусть к тек. моменту фирма выпустила 2 ц.б.:

1. обл. с 0 куп, номиналом F, на время T

2. акцию, див. не выплачиваются.

Основные предположения:

1. рынки совершенны, торговля непрерывна во времени

2. спот-цена определяется ГБД ds=(µS)dτ+(σS)dw_τ

3. безрисковая ставка одинакова для всех сроков и неизмен. во времени

4. отсутствует арбитраж

5. для ст-сти активов сущ-ет барьер Н. При его достижении начинается реорганизация. (Н<V₀)

6. издержки при реорганизации фирмы при достижении Н, а также в случае дефолта, равны К.

Оценка облигации.

1. Пусть Ф₁ – размер платежа держателям обл. в мом. T при условии, что ст-сть активов не пробивает барьер.

1. К≤F. Тогда:

Ф₁=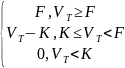

Ф₁=max{V_T-K;0}-max{V_T-F;0}+K*I(V_T-F)= , I(V_T-F)=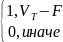

В силу отсут. арбитража, платеж совп. с платежом от портфеля, сост. из:

1. бар. опциона колл, выход. при понижении с ценой исп. К

2. кор. позиции по бар. опц. колл, вых. при понижении с ц. исп. F

3. К бар. бин. опционов с ц.и. F

Все опционы на активы фирмы

Привед. ст-сть платежа Ф₁ совп. со ст-стью портфеля:

PV(Ф₁)=С_do^T(V₀,K,H,t)- С_do^T(V₀,F,H,t)+K П_do^T(V₀,F,H,t)

2. К>F.

Ф₁=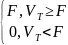

Такой же платеж у портфеля из F бин. бар. опционов

PV(Ф₁)=F П_do^T(V₀,F,H,t)

К*=min{K,F}

PV(Ф₁)= С_do^T (V₀,K*,H,t)- С_do^T(V₀,F,H,t)+K* П_do^T(V₀,F,H,t)

2. В нек. мом. t < τ ≤T пробивает барьер. Выясним чему равен платеж держателю обл-ции Ф₂ в мом. погашения в этом случае.

Рассмотрим мом. τ. V_τ=H

min{max{{H-K;0},F} – на такой платеж претендуют держатели облигации.

Доля кредиторов в активах 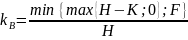. Тогда в момент Т кредиторы получают Ф₂=k_BV_T=k_Bmax{V_T-0;0}

Тогда имеем такой же платеж у портфеля и k_B бар. опции, вх. при понижении, с ц.и. 0.

PV(Ф₂)=k_B С_di^T (V₀,0,H,t)

Теорема 1. В усл. рассматриваемой модели тек. ст-сть обл. равна

B_t=С_do^T (V₀,K*,H,t)- С_do^T(V₀,F,H,t)+K* П_do^T(V₀,F,H,t)+ k_B С_di^T (V₀,0,H,t)

К*=min{K,F}, Д-во – все, что выше. ▪

Стоимость С_di^T (V₀,0,H,t).

, рассм.

,

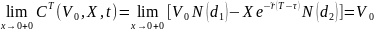
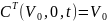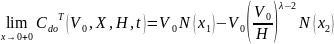
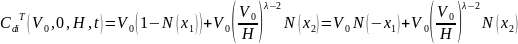
Оценка акции.

1. Барьер не пробивается

Ф₃ – платеж акционерам в момент погашения долгов в этом случае.

Ф₃=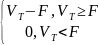

PV(Ф₃)= С_do^T (V₀,F,H,t)

2. Барьер пробит в мом. τ. V_τ=H

Ф₄ – платеж акционерам в момент погашения долгов в этом случае.

PV(Ф₄)=k_S С_di^T (V₀,0,H,t)

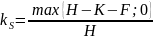- доля акционеров в момент τ.

Теорема 1. Стоимость акции в условиях модели находится по ф-ле:

S_t=С_do^T (V₀,F,H,t)+k_S С_di^T (V₀,0,H,t)

Д-во – выше. ▪

Следствие. Рын. стоимость фирмы ν_t в тек. момент

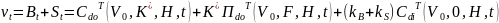
V₀≥ ν_t, V₀- ν_t =R_t – приведенная ст-сть ожид. издержек в случае реорганизации или дефолта.

Оценка корп. субординир. обл-ций с 0 купоном при наличии барьера.

К моменту t фирма выпустила 3 ц.б.:

1. Главную обл. с 0 куп, номиналом F_гл, на время T

2. Вторичную обл. с 0 куп, номиналом F_вт, на время T

3. акцию, див. не выплачиваются.

Рынки удовл. усл. пред. раздела.

Предп-я:

1. Ст-сть актива определяется ГБД dV=(µV)dτ+(σV)dw_τ, V_t(w)=V₀

2. Для стоимости акт. уст. барьер Н<V₀

3. Издержки К (при достижении Н или дефолте)

Оценка платежа по гл. обл-ции

1. Пусть Ф₁^гл – размер платежа держателям гл. обл. в мом. T при условии, что ст-сть активов не пробивает барьер.

1. К≤F_вт. Тогда:

Ф₁^гл=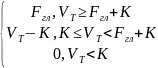

Ф₁^гл=max{V_T-K;0}-max{V_T-F_гл-К;0}

PV(Ф₁^гл)=С_do^T(V₀,K,H,t)- С_do^T(V₀,F_гл+К,H,t)

2. F_вт <К≤F_вт+ F_гл

Ф₁^гл=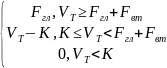

Ф₁^гл=max{V_T-K;0}-max{V_T-F_гл-F_вт;0}+(К-F_вт) I(V_т-F_гл-F_вт)

PV(Ф₁^гл)=С_do^T(V₀,K,H,t)- С_do^T(V₀,F_гл+F_вт,H,t) }+(К-F_вт) П_do^T(V₀,F_гл+F_вт,H,t)

3. К>F_вт+ F_гл

Ф₁^гл =

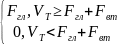
Ф₁^гл= F_гл I(V_т-F_гл-F_вт)

PV(Ф₁^гл)= F_гл П_do^T(V₀,F_гл+F_вт,H,t)

К*=min{K, F_гл+F_вт }

PV(Ф₁^гл)=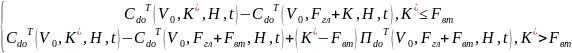

2. В нек. мом. t < τ ≤T пробивает барьер. Выясним чему равен платеж держателю гл. обл-ции Ф₂ в мом. погашения в этом случае.

Рассмотрим мом. τ. V_τ=H

min{max{{H-K;0},F_гл} – на такой платеж претендуют держатели гл. облигации.

.

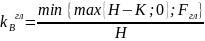Ф₂^гл =k_в^гл V_T= k_в^гл max{V_T-0;0}

PV(Ф₂^гл)= k_в^гл С_di^T (V₀,0,H,t)

Теорема 1. В усл. модели ст-сть гл . облигации с 0 куп.:

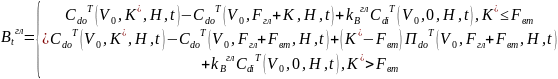
Оценка платежа по вт. обл-ции

1. Пусть Ф₁^вт – размер платежа держателям вт. обл. в мом. T при условии, что ст-сть активов не пробивает барьер.

1. К<F_вт. Тогда:

Ф₁^вт=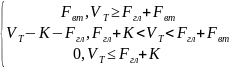

Ф₁^вт=max{V_T-K- F_гл;0}-max{V_T-F_гл- F_вт;0}+К I(V_т-F_гл-F_вт)

PV(Ф₁^вт)=С_do^T(V₀,K+ F_гл,H,t) - С_do^T(V₀,F_гл+F_вт,H,t)+К П_do^T(V₀,F_гл+F_вт,H,t)

2. К≥F_вт

Ф₁^вт=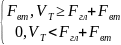

PV(Ф₁^вт)= F_вт П_do^T(V₀,F_гл+F_вт,H,t)

PV(Ф₁^вт)=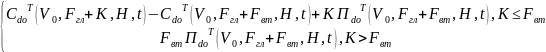

2. В нек. мом. t < τ ≤T пробивает барьер. Выясним чему равен платеж держателю вт. обл-ции Ф₂^вт в мом. погашения в этом случае.

Рассмотрим мом. τ. V_τ=H

.

Ф₂^вт =k_в^вт V_T= k_в^вт max{V_T-0;0}

PV(Ф₂^вт)= k_в^вт С_di^T (V₀,0,H,t)

Теорема 2. В усл. модели ст-сть вт . облигации с 0 куп.:

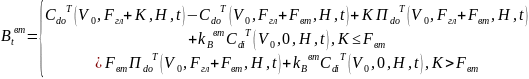
Оценка акции

1. Пусть Ф₁^акц – размер платежа держателям акц. в мом. T при условии, что ст-сть активов не пробивает барьер.

Ф₁^акц=

PV(Ф₁^акц)= С_do^T(V₀,F_гл+F_вт,H,t)

2. В нек. мом. t < τ ≤T пробивает барьер. Выясним чему равен платеж держателю акц. Ф₂^акц в мом. погашения в этом случае.

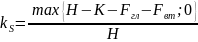, Ф₂^акц=k_s V_т

PV(Ф₂^акц)= k_s С_di^T(V₀,0,H,t)

Теорема 3. В усл. модели ст-сть акц.:

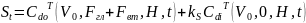
Следствие. Рын. стоимость фирмы ν_t в тек. момент

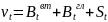
V₀≥ ν_t, V₀- ν_t =R_t – приведенная ст-сть ожид. издержек в случае реорганизации или дефолта.

Оценка корп. купонных облигаций при разрешенных и запрещенных продажах активов.

Ст-сть корп. куп. обл. при запрещенных продажах активов.

К тек. мом. t фирма выпустила 2 ц.б.:

1. обл. номиналом F, дата погашения Т. В мом. t₁, t₂, … , t_n вып-ся %-ты q₁, q₂, … , q_n (t < t₁ < t_{2 <} … < t_n=T)

2. обыкнов. бездив. акцию

Барьер Н выбир-ся так, что Н > max{q₁, … , q_n}

H < V₀

Прибыль облагается налогом TR

Обл-ции с 0 куп.

B_t=С_do^T (V₀,K*,H,t)- С_do^T(V₀,F,H,t)+K* П_do^T(V₀,F,H,t)+ k_B С_di^T (V₀,0,H,t)

К*=min{K,F},

Ст-сть потока платежей q_i в мом. t_i (если до t_i вкл. пробивается барьер, то % не выпл-ся) совпадает с

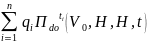
Теорема 1. Ст-сть корп. куп. обл-ции в тек мом. в усл. рассм. модели

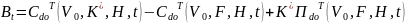
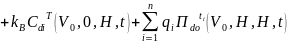
Оценка акции

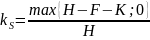
Теорема 2. Ст-сть акции в тек мом. в усл. рассм. модели

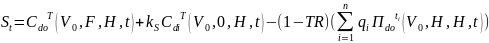
Следствие. Рын. стоимость фирмы ν_t в тек. момент

V₀≥ ν_t, R_t = V₀ + (TS)_t - ν_t – приведенная ст-сть ожид. издержек в случае реорганизации или дефолта.

«Налоговый щит»

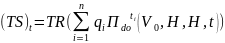
Ст-сть корп. куп. обл. при разрешенных. продажах активов.

К тек. мом. t фирма выпустила 2 ц.б.:

1. обл. номиналом F, дата погашения Т. %-ты выплачиваются непрерывно (в люб. мом. τ, t < τ ≤T ) в размере cF.

2. обыкнов. бездив. акцию.

1. В любой момент τ, t < τ ≤T, продается доля β активов фирмы. Ден. сумма βV_τ расходуется на оплату %-ов по долгам, а оставшаяся часть выплачивается в виде дивидендов.

2. Реорганизация фирмы до погашения обл-ции может произойти только, когда βV_τ не хватает для уплаты долгов с учетом выплач. налогов.

βV_τ > (1-TR) cF

V_τ > (1-TR) cF/β

H = (1-TR) cF/β

3. Ст-сть актива определяется ГБД dV=(µV)dτ+(σV)dw_τ, V_t(w)=V₀

Предположения:

1. Рынки совершенны

2. Сущ-ет безр. % ставка, одинаковая для всех сроков, не меняется во времени

3. Отсутствует арбитраж

Приведенные стоимости платежей различным участникам в мом. погашения обл. (Барьер не пробивается)

1. Приведенная ст-сть платежей держателям обл-ции

Совпадает со ст-стью обл. с 0 куп. номиналом F

С_do^T (V₀,K*,H,t)- С_do^T(V₀,F,H,t)+K* П_do^T(V₀,F,H,t)

К*=min{K,F}

Особенность – активы с пост. див. див. дох. β

2. Приведенная ст-сть платежей держателям акции

С_do^T (V₀,F,H,t)

3. Приведенная ст-сть платежей сторонним лицам

PV(Vт)- С_do^T (V₀,K*,H,t)- K* П_do^T(V₀,F,H,t)

V_т=max{V_т-0;0}, PV(Vт)= С_do^T (V₀,0,H,t)

Приведенная ст-сти промежуточных платежей при условии, что фирма платежеспособна, т. е. барьер не пробивался.

Обл.

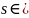. cF получ. держ. обл.

(cF) П_do^T(V₀,H,H,t)

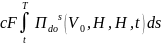- привед. ст-сть плат. всех держ. обл.

Акц.

.

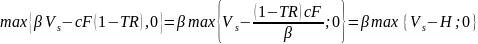
- прив. ст-сть платежей на мом. s

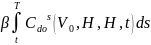
Сторонним лицам платежей не производится

Приведенная ст-сть платежей при реорганизации фирмы до даты погашения.

Обл.

В случае пробития держатель получает k_в долга

, k_в F(V₀). Привед. ст-сть активов F(V₀) на мом. T

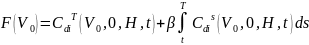
Акц.

, k_s F(V₀)

Стор. лица

, k_R F(V₀)

Теорема 1. В усл. рассм. модели ст-сть обл., выпущенной фирмой нах-ся след. образом:

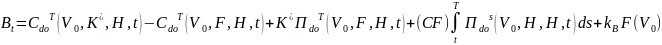
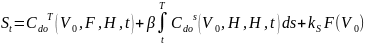
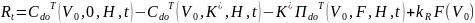
К*=min{K,F}, , ,

Недостаток теории: % ставка считается детерминированной.

17. Рисковая стоимость активов при заданном уровне доверия (VAR). Дельта-нормальный метод оценки рисковой стоимости.

Обозначим потери за время 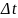через 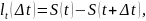где 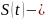стоимость активов в момент времени , .

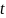Определение: Абсолютной рисковой стоимостью активов за время при уровне доверия 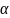называется денежная сумма .

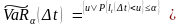Свойства:

1. P

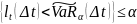
Доказательство:

Рассмотрим возрастающую последовательность 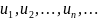, сходящуюся к .

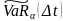Тогда .

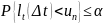неубывающая цепочка .

По теореме о непрерывности меры .

2. 

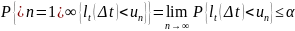Доказательство:

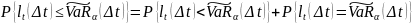
Рассмотрим убывающую последовательность , сходящуюся к .

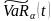Тогда .

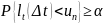невозрастающая цепочка .

.

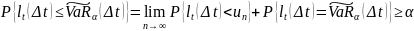Следствия:

1. Если возможные потери распределены непрерывно, то P .

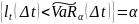2. P .

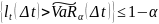Определение: Относительной рисковой стоимостью активов за время при уровне доверия называется денежная сумма .

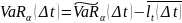измеряет все возможные потери, 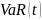– только непредвиденные.

Утверждение: .

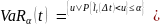Доказательство:

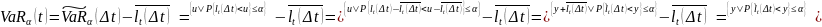
Свойства:

1. Если непредвиденные потери от актива A всегда меньше непредвиденных потерь B, то 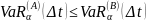(свойство монотонности).

2. При увеличении потерь от актива A в λ раз 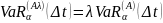(свойство однородности).

3. При добавлении к активу A безрискового актива B рисковая стоимость портфеля уменьшается: где r – реализуемая доходность активов¹, S_B – начальная цена безрискового актива B (свойство трансляционной инвариантности.

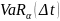не является когерентной мерой риска, так как не обладает свойством субаддитивности (не позволяет в полной мере учесть эффект диверсификации).

Дельта-нормальный метод оценки VaR

Рассмотрим некоторые активы и предположим, что стоимость этих активов в любой момент времени t есть функция от этого момента времени и рыночных факторов :

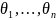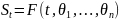
Факторы:

• стоимости базовых активов;

• обменные курсы;

• процентные ставки;

• доходности рыночных индексов.

Будем считать, что 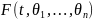– дифференцируемая функция.

Введем обозначения:

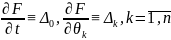
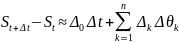
Предполагается, что сами факторы, а, следовательно, и их изменения распределены нормально. Значит доход распределен нормально. .

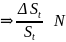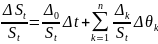
Если РДА распределена нормальн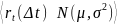о , то

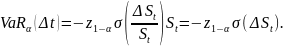
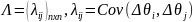
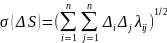
Основная проблема метода – оценка корреляционно-дисперсионной матрицы .

На основании исторических данных оценивают 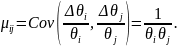Тогда .

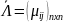Качество оценки зависит от следующих факторов:

1. точность оценки ;

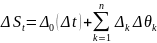2. точность оценки матрицы (для ее оценки используются метод скользящего среднего, GARCH, МГК (для больших портфелей); факторные модели);

3. близость распределения каждого фактора риска к нормальному.

Пример 1:

Оценка VaR в форвардных контрактах на обмен валюты:

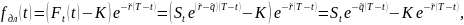
где – безрисковая процентная ставка, – дивидендная доходность валюты.

Факторы риска: , .

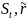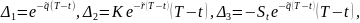
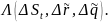
Пример 2:

Рассматривается портфель облигаций без риска дефолта. Считается, что кривая рыночных доходностей перемещается параллельно. Величина этого сдвига 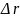распределена нормально с дисперсией .

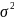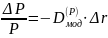
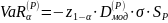
Пример 3:

Рассматривается купонная облигация с полугодовыми купонами, до погашения которой n полугодовых периодов.

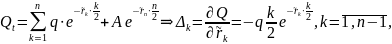
Проблема: нужна ковариационная матрица изменений всех процентных ставок.

Пример 4:

Рассматривается хорошо диверсифицированный портфель акций. Однофакторная модель рынка: где 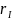– доходность индекса. 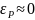, так как портфель хорошо диверсифицирован. Можно предположить, что распределена нормально, а 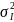– дисперсия реализуемой доходности рыночного индекса.

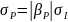– стандартное отклонение реализуемой доходности рассматриваемого портфеля.

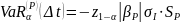
Пример 5:

Оценка рисковой стоимости европейского опциона в модели Блека-Шоулса.

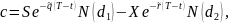
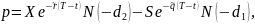
где .

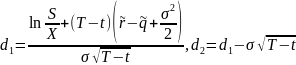Факторы риска: 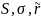, . Далее находятся производные c и p по всем факторам риска. Это и будут дельта-коэффициенты.