Оглавление

11. Дельта и гамма хеджирование опционных позиций. 27

12. Модель Мертона для оценки корпоративных ценных бумаг. 29

29. Операционный риск 82

Классификация операционных рисков 82

Методы оценки операционного риска 82

Стандартизованная методика TSA 83

4.3.2. Альтернативный стандартизованный метод 84

В целом совпадает со стандартизированным подходом, однако, по двум направлениям (розничный и коммерческий банкинг) в качестве индикатора риска выступает не валовой доход по направлению, а средний за 3 года размер активов (непогашенных кредитов), умноженный на фактор . При этом бета-коэффициенты такие же. 84

4.4. Усовершенствованные методы измерения 84

1. 1. Дюрация и выпуклость финансовых инструментов с фиксированными доходами

Пусть по облигации без риска дефолта в моменты t₁, t₂, ... , t_n выплачиваются, соответственно, денежные суммы C₁, C₂, ..., C_n. Внутренняя доходность облигации при начислении процентов m раз в год равна r. Тогда текущая стоимость облигации равна:

Если внутренняя доходность облигации изменится на величину r, то ее новая стоимость равна:

Изменение стоимости облигации можно записать приблизительно:

Или:

Легко найти:

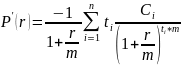
Дюрацией (Маколея) облигации называется число:

Выпуклостью (Маколея) облигации называется число:

Тогда изменение ст-сти обл при изменении ее внутренней дох-сти на можно записать в виде:

Или:

Свойства дюрации и выпуклости:

1. Дюрация любой облигации не превышает срока до ее погашения. Дюрация чисто дисконтной облигации равна сроку до ее погашения.

2. Если облигация не является чисто дисконтной, то чем больше внутренняя доходность облигации, тем меньше дюрация и выпуклость этой облигации.

3. Если все платежи по облигации отсрочить на одно и то же время , то ее дюрация увеличится на , а выпуклость на .

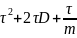4. Если r - внутренняя доходность облигации при начислении процентов m раз в год, то

2. 2. Эффективная граница множества инвестиционных возможностей при заданном наборе рискованных активов

Пусть на рынке имеются ценные бумаги n видов с ожидаемыми доходностями r₁, r₂, …, r_n, а ковариационная матрица доходностей этих ценных бумаг равна:

Будем считать, что столбцы этой матрицы образуют систему линейно независимых векторов, а среди чисел r₁, r₂, ... , r_n есть несовпадающие.

Для отыскания портфеля с наименьшим риском при заданной ожидаемой доходности r необходимо решить задачу:

Так как среди чисел r₁, r₂, ... , r_n есть несовпадающие, то система всегда имеет решение. Так как функция положительно определена, то система имеет единственное решение.

Теорема: существуют числа a_i, b_i такие что вектор является оптимальным решением.

Доказательство: Функция Лагранжа имеет вид:

Ищем производные по всем переменным, а далее методом гаусса решаем систему линейных уравнений.

В итоге получаем, что столбец свободных членов имеет вид, как в доказываемом векторе. Что и требовалось доказать.

Следствие 1: Множество инвестиционных возможностей определяется уравнением вида: где A > 0, C > 0, B² - 4AC < 0

Следствие 2: Эффективная граница множества инвестиционных возможностей при разрешенных коротких продажах ценных бумаг определяется уравнением вида:

3. Эффективная граница множества инвестиционных возможностей при наличии безрискового актива.

Предположим, на рынке имеются рискованные активы n видов с ожидаемыми доходностями и некоторый безрисковый актив с доходностью .

Пусть - множество допустимых портфелей из данных рискованных активов. Тогда можно определить множество инвестиционных возможностей и его эффективную границу при использовании данных ценных бумаг.

Если инвестор может неограниченно предоставлять кредиты и брать ссуды под безрисковую ставку , то множество его инвестиционных возможностей совпадает с множеством вида:

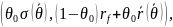
Где

Эффективную границу этого множества инвестиционных возможностей обозначим через

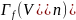
Теорема. Предположим, что инвестор инвестор может неограниченно предоставлять кредиты и брать ссуды под одну и ту же безрисковую ставку

Если инвестиционная возможность , где

попадает на эффективную границу , то

1. Инвестиционная возможность

2. Эффективная граница совпадает с лучом, заданным уравнением:

Определение. Портфель назовем касательным портфелем, соответствующим безрисковой процентной ставке , если существует положительное число такое, что

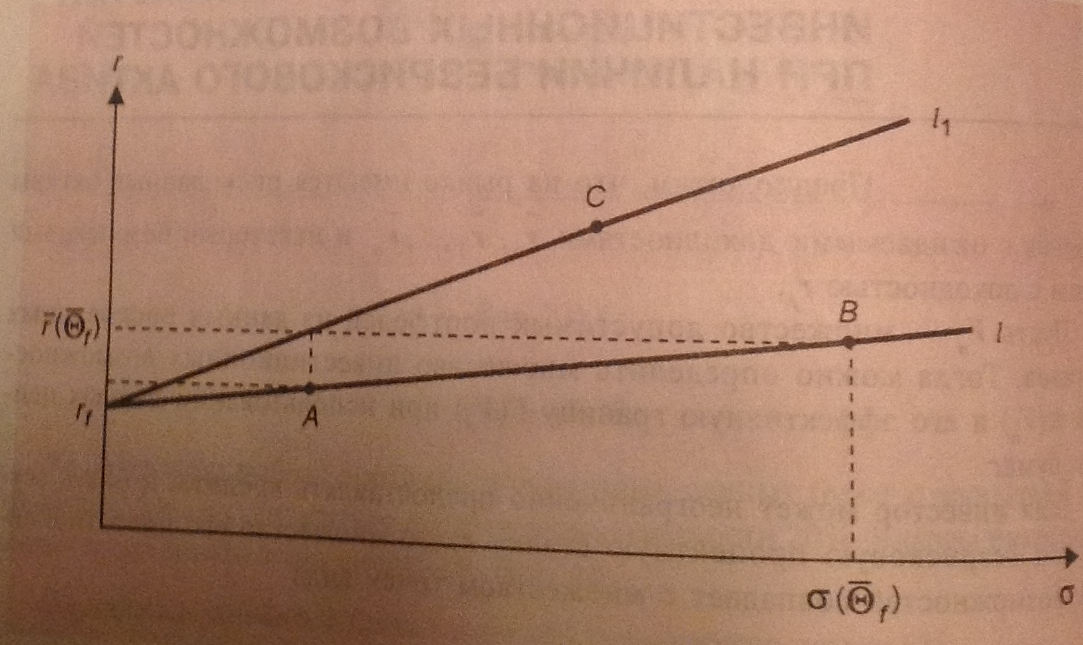
Следствие. Если не существует касательного порфеля, соответствующего безрисковой процентной ставке , то эффективная граница либо состоит из одной точки (0, ), либо является пустым множеством.

Отметим основные свойства касательного портфеля соответствующего безрисковой процентной ставке :

1. Касательный портфель всегда определяет инвестиционную возможность, принадлежащую эффективной границе

2. Если инвестор может неограниченно предоставлять кредиты и брать ссуды под безрисковую ставку , то эффективная граница совпадает с лучом

Где – ожидаемая доходность касательного портфеля

– стандартное отклонение касательного портфеля

3. Имеет место равенство

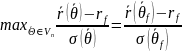
Теперь рассмотрим более реальную ситуацию, когда инвестор может предоставлять кредиты под безрисковую ставку , а брать ссуды под безрисковую ставку , причем

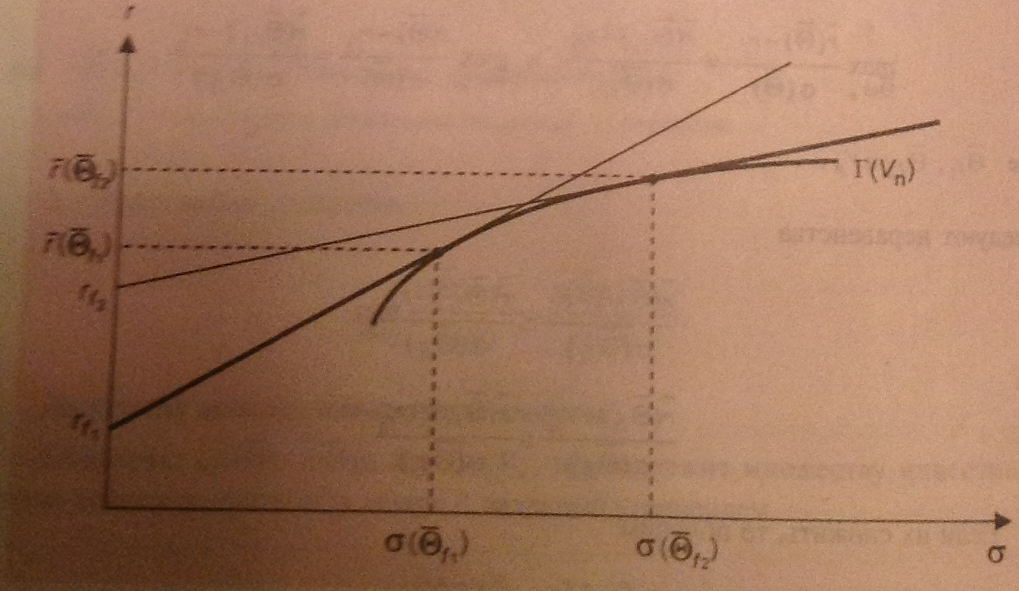
Тогда при существовании касательный портфелей , соответствующих этим безрисковым ставкам, эффективная граница множества инвестиционных возможностей определяется условиями: