36.Классическая и обобщенная модели множественной линейной регрессии. Условия применения метода наименьших квадратов, свойства его оценок.

Основная цель множественной регрессии - построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также их совокупное влияние на результативный признак.

Для двухфакторной модели уравнение множественной линейной регрессии: .

Чтобы знать, можно ли применять метод наименьших квадратов (МНК) для оценки параметров, существуют следующие предпосылки (условия) применения МНК:

1.Y-зависимая величина является случайной (эндогенной) переменной; X – фиксированная, заданная величина (экзогенная)

2.Математическое ожидание остатков д.б. =0., т.е. М(Ei)=0. (Для справки: матем.ожидание – это аналог средней и это же есть ковариация).

3.Остатки д.б. гомоскедастичны (дисперсия остатков одинакова для всех значений фактора). Тесты на гетероскедастичность проводят (тест Уайта, тест Глейзера), если не подтверждается, то делаем вывод о гомоскедастичности.

4.Отсутствие автокорреляции остатков (то есть остатки распределены независимо друг от друга, нет связи между предыдущим и последующим), т.е. М(Еi Еj)=0. Тест на автокорреляцию остатков – это тест Дарвина-Уотсона.

Если выполняются все 4 условия, то модель будет называться классической моделью линейной регрессии.

5.Остатки подчиняются нормальному закону распределения.

Если выполняются все 5 условий, то модель уже будет называться классической нормальной моделью линейной регрессии.

6.Отсутствие коллинеарности между факторами (отсутствие связи между ними).

Последнее условие (6) если выполняется, то модель можно отнести к множественной регрессии.

Если нарушается 3 и 4 предпосылки (одновременно или одна из них), то речь идет уже об обобщенной модели регрессии. Если 3 условие НЕ выполняется, а 4 выполняется, то можно применять Взвешенный метод наименьших квадратов (ВМНК).

Модель: . Найдем параметры модели с помощью МНК, согласно которому составим систему уравнений:

Решение: ; (b-коэфф. парной (чистой) регрессии);

где ; ; 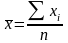; ( ); n – число наблюдений

Свойства оценок МНК: 1. Св-во несмещенности ( означает, что математическое ожидание выбранных оценок параметров =0); 2. Св-во состоятельности. Оценки считаются состоятельными, если их точность увеличивается с увеличением объема выборки, т.е. чем больше выборка, тем меньше ошибок. Поэтому на каждый фактор примерно по 10 наблюдений должно быть. 3. Св-во эффективности (оценки характеризуются наименьшей дисперсией или ошибками, когда в остатках гетероскедастичность, то это свойство нарушается и тогда оценки уже неэффективные).

37.Прогноз и оценка его точности на основе уравнений парной и множественной линейной регрессии.

При осуществлении прогноза в модель регрессии подставляем прогнозное значение Х и получаем прогнозное значение У. Для этого можно использовать только качественные модели (в них высокий коэф. Детерминации (показывает ск-ко % вариации У зависит от учтенных в модели факторов) и параметры значимы).

При использовании уравнения множественной регрессии в целях прогнозирования необходимо давать точечную и интервальную оценку полученных прогнозных значений зависимой переменной.

Средняя ошибка для индивидуального прогноза: (для парной линейной регрессии)

Средняя ошибка для среднего прогноза:

Для прогноза Х выбирается из: Х min≤ Xn≤Xmax Предельная ошибка прогноза:

Доверительные границы определяются: