План

1. Зростання і спадання функції.

• Ознаки зростання і спадання функції на деякому проміжку.

• Дослідження функції на монотонність.

2.Екстремальні точки. Локальний екстремум функції.

• Поняття екстремуму функцій та локального екстремуму функції.

• Необхідна умова екстремуму функції.

• Достатня умова екстремума функції.

3. Знаходження найбільшого і найменшого

значення функції.

• Алгоритм знаходження найбільшого і найменшого значень функції.

• Алгоритм знаходження найбільшого і найменшого значень функції під час розв’язання прикладних задач.

• Загальна схема дослідження функції і побудови її графіка.

Зростання і спадання функції.

• Ознаки спадання та зростання функції на деякому проміжку.

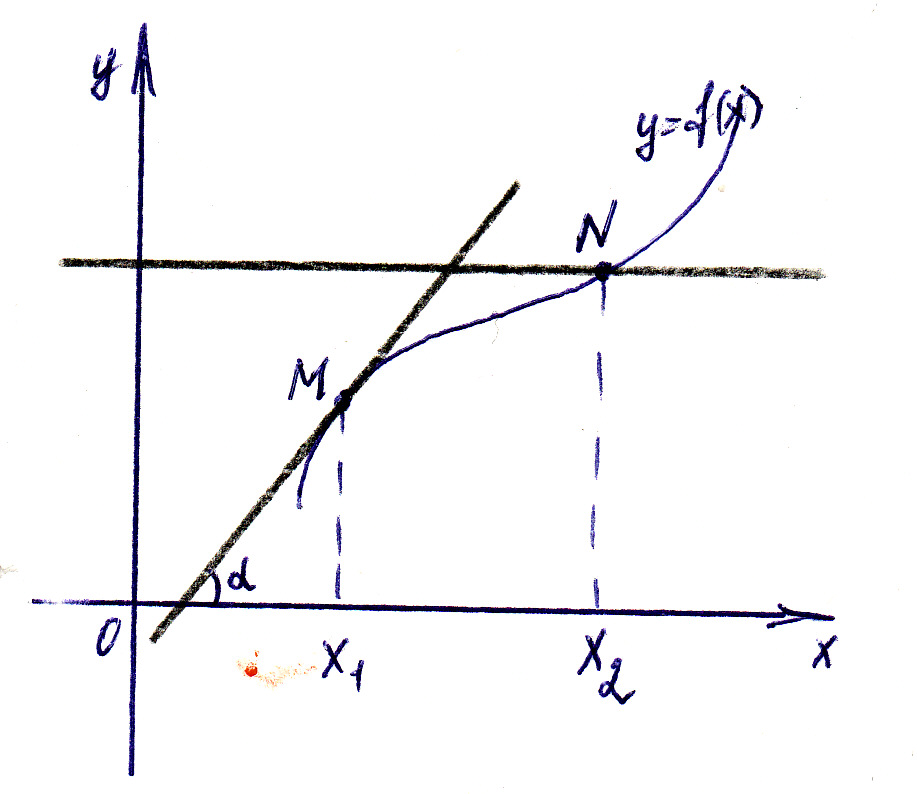
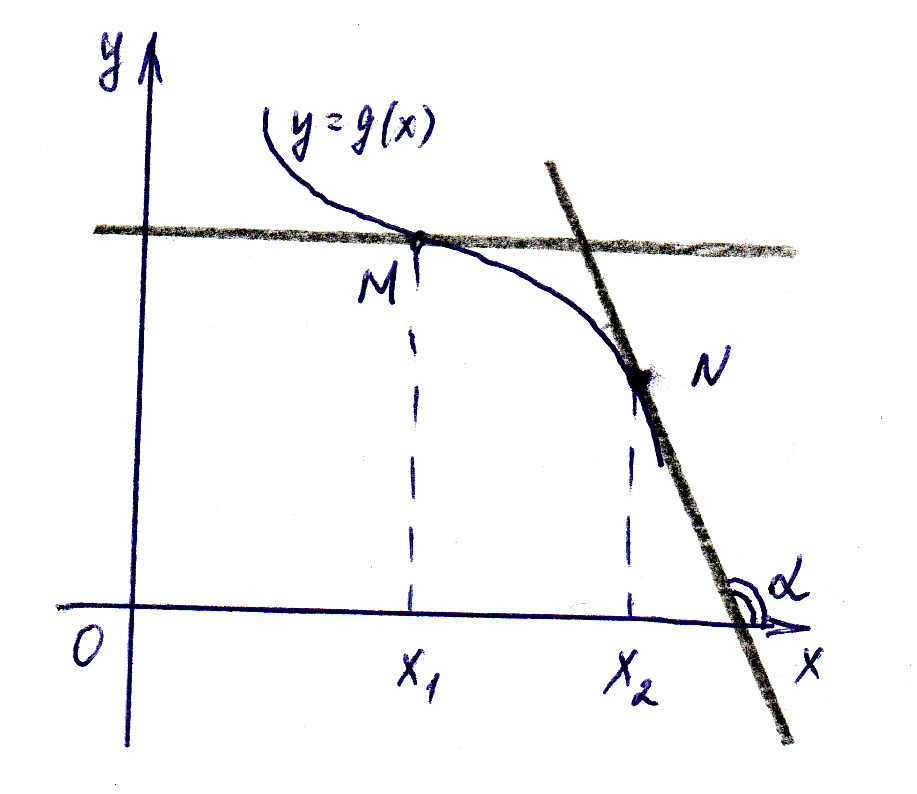
а б

Розглянемо дотичні до графіка зростаючої функції y=f(x) (див. рис. а), проведені в точках з абцисами x₁ і x_2. У точці x₁ кут α гострий, tg α>0, k=f '(x₁) >0. У точці x₂ k=0, або дотична паралельна осі ОХ, тобто k=f '(x₂) =0. Отже, f '(x) ≥0, якщо y=f(x) зростає.

Розглянувши графік спадної функції y=g(x) (див. рис. б), аналогічно дійдемо висновку, що k≤0 в точках з абцисами x₁ і x₂ і відповідно, бо дотична у точці x₂ кут α тупий. Отже, f '(x) ≤0, якщо y=f(x) спадає.

• Дослідження функції на монотонність.

Проміжки зростання і спадання функції часто називають проміжками монотонності функції. Для практики дуже важливо те, що справедливі й обернені теореми, які показують, як за знаком похідної можна встановити характер монотонності функції на проміжку. При цьому, щоб не виникало недоречності, беруть тільки відкриті проміжки - інтервали, або відкриті промені.

Теорема 1(обернена). Якщо в кожній точці відкритого проміжку (а; b) виконується нерівність f '(x) ≥0 (причому рівність f '(x) =0 виконується лише в окремих точках і не виконується ні на якому проміжку [m,n] з інтервалу (a;b) ), то функція y=f(x) зростає на проміжку (a;b).

Теорема 2(обернена). Якщо в кожній точці відкритого проміжку (а; b) виконується нерівність f '(x) ≤0 (причому рівність f '(x) =0 виконується лише в окремих точках і не виконується ні на якому проміжку [m,n] з інтервалу (a;b) ), то функція y=f(x) спадає на проміжку (a;b).

Дослідити функцію на монотонність - це значить з’ясувати, на яких проміжках області визначення функції зростає, а на яких - спадає. Згідно з теоремами 1 і 2 пов’язаної зі знаком похідної.

Звертаємо увагу!

Як дослідити функцію на монотонність:

1. Знайти f '(X)

2. Якщо на проміжку (a;b) виконується нерівність f '(x) ≥0, то функція y=f(x) зростає на проміжку (a;b).

3. Якщо на проміжку (a;b) виконується нерівність f '(x) ≤0, то функція y=f(x) спадає на проміжку (a;b).

А що буде, якщо на проміжку (a;b) f '(x) =0? Мабуть, функція y=f(x) ані зростає, ані спадає.

Що це за функція? Відповідь очевидна: у=С (константа або стала величина).

Теорема 3. Якщо в кожній точці відкритого проміжку (а; b) виконується рівність f '(x) =0 , то функція y=f(x) є сталою в цьому проміжку (a;b).

Пояснення на прикладах.

Приклад 1. Довести, що функція f(x)=x⁷+4x³-11 зростає на всій числовій прямій.

Розв’язання: f '(x)=7x⁶+12x² . Для всіх х R виконується нерівність f '(x) ≥0, бо 7x⁶+12x²≥0, якщо х R, причому f '(x) =0 тільки в одній точці х=0. Таким чином, згідно з теоремою 1 функція y=f(x) зростає.

Приклад 2. Довести, що функція у=9 cos x+sin 2x-18x на всій числовій прямій.

Розв’язання: у '=9(-sin x)+2 cos 2x-18= - 9sin x+2 cos 2x-18 .

- 9sin x ≤9, cos 2x≤2, тоді - 9sin x+2 cos 2x ≤ 11, отже, - 9sin x+2 cos 2x -18≤ - 7. Тобто - 9sin x+2 cos 2x -18<0. Ця нерівність виконується для всіх х R .Таким чином, згідно з теоремою 2, функція y=f(x) спадає на всій числовій прямій.

Приклад 3. Розв’язати рівняння 9 cos x+sin 2x-18x=х³+9.

Розв’язання: Як було доведено в прикладі 2, функція у=9 cos x+sin 2x-18x спадна. Функція g= х³+9 - зростаюча, бо g' = 3х² ≥0 для х R, а g' = 0 в точці х=0 - лише одній. Має місце теорема 2 про корінь рівняння. Тоді рівняння y=g(x) має один корінь, який легко дібрати : х=0. Дійсно, 9 cos 0+sin (2*0) - 18*0=0³+9*0; 9=9 - істинне .

Відповідь: 0.

Приклад 4. Дослідити функцію у=4х³+6х²-8 на монотонність.

Розв’язання:

1. D (y)=R;

2. у '= 12x²+12 x=12x (x+1);

3. 12x (x+1)>0, якщо х(х+1)>0;

12x (x+1)<0, якщо х(х+1)<0;

4. Розв’яжемо кожну з нерівностей методом інтервалів:

g(x)=х (х+1); D (g)=R,

нулі: g(x)=0, х (х+1)=0, х₁=0, х₂= - 1.

g(x)>0, якщо х ( - ∞;- 1) і х ( 0; + ∞);

g(x)<0, якщо х ( - 1; 0).

Отже функція у=4х³+6х²-8 зростає, якщо

х ( - ∞;- 1) і х ( 0; + ∞); спадає , якщо

х ( - 1; 0).

Відповідь: ( - 1; 0) - інтервал спадання функції, ( - ∞;- 1) і х ( 0; + ∞) - інтервали зростання.