Расчет погрешности мертвого хода передачи

Передаточный коэффициент j-й элементарной передачи:

Минимальное значение мертвого хода: ,

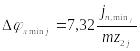– минимальный боковой зазор между зубьями по общей нормали к профилям, выбирается по таблицам [1]

Максимальное значение мертвого хода:

, где

– наименьшее смещение исходного контура шестерни и колеса

– допуск на смещение исходного контура шестерни и колеса

– допуск на отклонение межосевого расстояния передачи

– радиальные зазоры в опорах шестерни и колеса.

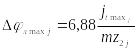
Координаты середины поля рассеяния мертвого хода :

Поле рассеяния мертвого хода :

№	1	2	3	4		5	6		7	8		9	10		11	12		13	14
jn,min, мкм	13		13		13			13			13			13			13
	0.001		0.00317		0.01			0.0316			0.1			0.316			1
л мin угл.мин	1.15		1.15		1.15			1.15			1.15			1.15			1.15
лмах, угл.мин	6.85		6.85		6.85			6.85			6.85			6.85			8.85

E^p_лΣ=6.18’

Так как процент принятого риска , то

Вероятностное значение мертвого хода кинематической цепи

Вероятная суммарная погрешность ЭМП

Условие (14.07’<[20’]) выполняется, следовательно, ЭМП может обеспечить заданную точность.

10.Проверочные расчеты Проверочные расчеты на прочность Проверка прочности зубьев на контактную и изгибную прочность

Контактные напряжения, действующие на зубчатые колеса

,

изгибные напряжения, действующие на зубчатые колеса

, где

i₁₂ – передаточное отношение ступени;

M₂ – момент на колесе;

a – межосевое расстояние;

b – ширина зубчатого колеса, т.к. ширина колеса меньше ширины шестерни, то при расчетах на прочность используем ширину колес b = 5 мм.

K – коэффициент расчетной нагрузки;

K_конт = K_HVK_Hβ при расчете на контактную прочность

K_изгибн = K_FVK_Fβ при расчете на изгибную прочность

K_HV, K_FV – коэффициент динамической нагрузки

K_FV =1.2

K_Fβ, K_Hβ – коэффициент неравномерности распределения нагрузки по ширине зуба

K_Fβ =1,05, т.к. колеса расположены между опорами [1]

K_изгибн = K_FVK_Fβ = 1.2·1.05 = 1.26

K_конт = K_HVK_Hβ = 1.1·1.03 = 1.13

(Е₁ = E₂ = 2.1·10⁵ МПа для материалов шестерни и колеса)

Проверку ведем для наиболее нагруженной ступени редуктора

Проверка на контактную прочность:

(МПа)

МПа

МПа

, т.е. зубчатые колеса удовлетворяют условиям контактной прочности

Проверка на изгибную прочность:

(МПа)

МПа МПа

, т.е. зубчатые колеса удовлетворяют условиям изгибной прочности

11.Расчет предохранительной муфты

В качестве муфты возьмём кулачковую предохранительную муфту

Параметры муфты

– число кулачков

– угол профиля кулачка

– ширина кулачков

– высота кулачков

– средний диаметр приложения силы к кулачкам

– передаваемый вращающий момент

Размеры муфты

– наружный диаметр муфты

– диаметр вала

В качестве материала муфты выберем сталь 20Х ГОСТ 4543-71 (М59)

Термообработка: объемная закалка

 = 7,85 г/см³

– предел прочности

– предел текучести

HRC = 52

Проведем расчет на контактную прочность и на изгиб.

Допускаемый вращающий момент по контактным напряжениям:

– средний диаметр кулачков;

– число кулачков;

– ширина кулачков;

– высота кулачков;

– допускаемое номинальное давление, принимают равным .

– условие выполнено

Допускаемый вращающий момент по изгибу

– расчетное число кулачков, равное 1/2 – 1/3 общего числа кулачков;

– допускаемое напряжение на изгиб, выбирают по пределу текучести с запасом не ниже : ;

– толщина кулачков у основания, при беззазорном зацеплении:

– угол наклона рабочих граней, практически принимают не более .

– условие выполнено

Определение потребной силы сжатия пружины при мгновенных перегрузках:

– расчетный вращающий момент ( – наибольший номинальный вращающий момент);

– угол трения между кулачками (для стали );

– коэффициент трения в шпоночном соединении (для стали ).

Примем и .

Потребная сила сжатия пружины:

Подбор среднего диаметра пружины , диаметра проволоки и числа рабочих витков производят, используя уравнения прочности и жёсткости

– максимальная сжимающая сила(возьмем )

– индекс пружины

– коэффициент увеличения напряжения у внутренней стороны витка (сравнительно с напряжением, возникающим при кручении прямого стержня)

– жесткость пружины

–величина допускаемого касательного напряжения при кручении;

– модуль упругости первого рода (Юнга).

Зададимся значением , тогда по графику из [3] . В качестве материала выберем стальную пружинную проволоку, для которой

Получаем , примем

Пусть в пружине рабочих витков, тогда ее жесткость

Посчитаем начальную высоту пружины по соотношению:

– коэффициент, который определяется зазором между витками в её наибольшем сжатом состоянии (выберем );

– число концевых витков (возьмем );

– наибольшее перемещение конца пружины

Получаем