2 Расчет цилиндрической зубчатой передачи

2.1 Расчет закрытой зубчатой косозубой передачи.

2.1.1 Материалы колес.

Для колеса и шестерни принимаем сталь 40х. Термическая обработка - улучшение.

Твердости: для колеса -260.. .280 НВ, для шестерни- 230...260 НВ.

В качестве расчетной контактной твердости материала принимаем ее среднее значение, так как вероятность обеспечения ресурса не задана.

Для шестерни (2, с.59): НВ₁=0,5*(НВ_min+НВ_max)=0,5*(230+260)=245МПа;

Для колеса: НВ₂=0,5*(НВ_min+НВ_max)=0,5*(260+280)=270Мпа

2.1.2 Допускаемые контактные напряжения.

Предел контактной выносливости зубьев: σ_Hlimb=2НВ_ср+70

Для шестерни σ_Hlimb= 2*245+70 =610МПа,

Для колеса σ_Hlimb= 2*270+70 = 560 МПа.

L_h= - расчетный ресурс работы привода;

L_h=365*24*L*K_r*K_c

L= 10 лет - срок службы привода;

К_г = 0,7 - коэффициент годовой загрузки;

К_с = 0,35 - коэффициент суточной загрузки;

L_h=365*24*10*0,7*0,35=21500 часов

Расчетное число циклов напряжений при заданной графике нагружений

N_k =60*с *n *L_h,

где n- частота вращения колеса, по материалу которого определяем допустимые напряжения;

с =1 - число зацеплений зуба за один оборот колеса;

Тогда для шестерни N_k1 = 60*1*1140*21500 =1470 *10⁶ циклов,

для колеса N_k2 = 60*1*160,56*21500 =207*10⁶ циклов.

Базовое число циклов напряжений в зависимости от твердости материала

N_Hlim1=20*10⁶ циклов,

N_Hlim2=16*10⁶ циклов

Определяем коэффициент долговечности Z_N при расчете по контактной выносливости при N_k> N_Hlim1

Для шестерни

Для колеса

Определяем допустимые контактные напряжения по формуле σ_НР=

где S_Hmin=1,1 - коэффициент запаса прочности.

Для шестерни σ_НР=

для колеса σ_НР=

Допускаемое напряжение на изгиб определяется по формуле:

[1, c.62],

где - базовая прочность зубьев на изгиб, =1,75НВ_ср

S_F – коэффициент запаса прочности при изгибе, S_F=1,7

Y_N – коэффициент долговечности при изгибе

Базовое число циклов при изгибе для всех сталей принимается, =4*10⁶ т.к , то принимается Y_N1= Y_N2=1.

Для шестерни

Для колеса

2.1.3 Геометрические параметры ступени.

Определим межосевое расстояние.

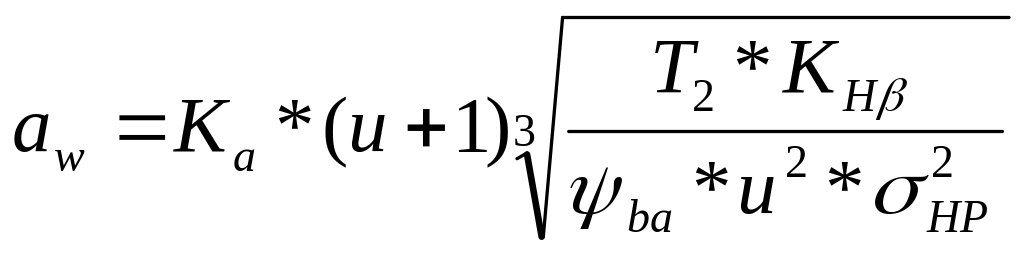
где K_а – коэффициент межосевого расстояния, для косоозубых передач K_а= 430;

K_Hβ – коэффициент изменения нагрузки при контактной прочности по длине зуба, в предварительных расчетах K_Hβ=1,1…1,2;

u – передаточное число, u=7,1;

Ψ_ba – коэффициент ширины зуба относительно межосевого расстояния, Ψ_ba=b_w/a_w, для симметрично расположенных колес относительно опор Ψ_ba=0,5…0,6, а несимметрично Ψ_ba=0,3…0,4;

σ_НР – расчетное допустимое напряжение материалов колес, σ_НР= σ_НР2→min σ_НР=468,4.

Тогда

Принимаем a_w = 125 мм по ГОСТ 2185-66.

Определяем необходимую ширину зубчатого венца колеса:

b_w=Ψ_а *a_w =125*0,25=31,3мм

Выбираем ширину колеса из нормального ряда b_w=32 мм.

Принимаем значение нормального модуля зубчатых колес в пределах: m_n=(0,01... 0,02)*a_w =(0,01... 0,02)*125=1,25...2,5.

В соответствии с ГОСТ 9563-60 назначаем m_n=1,5 мм.

Предварительно принимаем угол наклона зубьев 14º,53΄ и проверяем условие двухпарного зацепления:

b_w=32мм≥ мм -условие выполняется.

Определим суммарное число зубьев шестерни и колеса.

Z_Σ = Z₃ + Z₄ = 2*a_w*cos14º53΄/2 = 2*125*cos14º,53΄/2 =161,6 Принимаем Z_Σ=161.

С целью сохранения стандартных значений межосевого расстояния и модуля корректируем угол наклона зубьев:

Определим число зубьев шестерни.

Z₁= Z₂/(l + u) =161 /(1+7,1)=20,6

Принимаем Z₁ = 20.

Условие не подрезания зуба выполняется Z₁ > Z_min=17*cos³β.

35 >17cos³14,9836° =15

Определим число зубьев колеса.

Z₂ = Z_Σ-Z₃ = 161-20=141

Определим основные геометрические параметры передачи, мм:

Делительный диаметр:

шестерни d_w1=m_n* Z₁/cosβ = 1.5*20/cos14.9836°=30.9мм

колеса d_w2 = m_n*Z₂/cosβ =1.5*141/ cos14.9836 °=218.3мм

Диаметр вершин зубьев:

шестерни d_a1= d_w1 + 2*m_n = 30.9+2*1.5= 33.9мм

колеса d_a1 =d_w2 + 2*m_n = 218.8+2*1.5=221.8 мм

Диаметр впадин зубьев:

шестерни d_fl = d_w1 -2,5*m_n = 30.9-2,5*1.5=26 мм

колеса d_f2 = d_w2 - 2,5*m_n = 218.8-2,5*1.5=214 мм

Ширина колеса b₂= b_w=32мм

b₁ = b₂ + (1...2)мм

b₁ =32+1=33мм

Проверим межосевое расстояние.

a_w = 0,5*(d_w1 + d_w2) = (30.9+218.8)=124.6 мм

2.1.4 Проверочный расчет зубьев на контактную прочность.

Согласно ГОСТ 21354-87 расчет выполняют по условию

Контактное напряжение находим по формуле

,

где Z_E - коэффициент, учитывающий механические свойства материалов сопряженных зубчатых колес, для стали Z_E=190 Мпа;

Z_H - коэффициент, учитывающий форму сопряженных поверхностей зубьев, при α=20^º, β=14,53^º

Z_ε -коэффициент, учитывающий суммарную длину контактных линий, для косозубых колес: Z_ε = ,

где - коэффициент торцевого перекрытия зубьев, определяемый по выражению

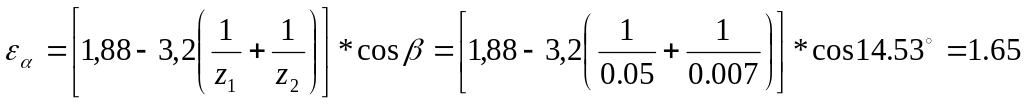
F_t- окружная сила: F_t = 2T₁/d₂ = 2*11,83*10³/41,3 =572,9H

Коэффициент нагрузки определяем по формуле

К_н = K_A*K_Hβ*K_Hα*K_Hυ = 1,54*1,03*1,14*1,05 =1,54,

где К_А коэффициент внешней динамической нагрузки табл.5.4 (2, с.64) К_А=1,54;

К_Нβ- коэффициент, учитывающий неравномерность распределения нагрузки по длине контактной линии согласно рис.5.7.(2, с.64), при Ψ_bd=b₂/d₁=32/41.3≈0.77 и выполнении передачи по схеме 6, твердость НВ<350, К_Нβ=1,03;

К_Hα- коэффициент, учитывающий распределение нагрузки между зубьями, по рис. 5.8 (2, с. 65)

Степень точности изготовления колес, n_ст=9 К_Hα=1,14;

K_Hυ-коэффициент динамичности нагрузки, K_Hυ=1,05

Тогда

Определяем степень недогрузки материала по контактным напряжениям:

т.к. нагрузка меньше 15% то результат допустим.

2.1.5 Проводим проверочный расчет по напряжению изгиба.

Для предотвращения усталостного излома шестерни и колеса следует соблюдать условие:

σ_F ≤ σ_FP,

где σ_F- расчетное местное напряжение изгиба в опасном сечении;

σ_FP- допустимое напряжение.

Условие прочности на изгиб имеет вид (1, с.68)

где K_F-коэффициент нагрузки при изгибе,

K_F=K_A*K_Fβ*K_Fα*K_Fυ=1.25*1.38*1*1.08=1.9

K_A-коэффициент внешней динамической нагрузки табл.5.4 (2, с.64), K_A=1.25;

K_Fβ- коэффициент, учитывающий неравномерность распределения нагрузки по длине контактной линии при изгибе согласно рис. 5.7. (2 с.64), при Ψ_bd=1.23 и выполнении передачи по схеме 6, НВ≤350, K_Fβ=1,38;

K_Fα-коэффициент, учитывающий распределение нагрузки между зубьями (1с. 69), K_Fα=1;

K_Fυ-коэффициент динамичности нагрузки при изгибе, n_ст=9, НВ≤350, υ=1,8м/с, K_Fυ=1,08.

Коэффициент формы зуба Y_FS выбираем в зависимости от количества зубьев эквивалентного колеса:

для шестерни z_v1= - Y_FS1=4.48 (2, c.67)

для колеса z_v2= - Y_FS2=3,6 (2, c.67)

Коэффициент, учитывающий наклон зуба:

где ε_β-коэффициент осевого перекрыти

Коэффициент, учитывающий перекрытие зубьев:

Меньшую прочность имеют зубья колеса.

2.1.6 Силы в зацеплении

Окружная сила: F_t1= -F_t2=2*T₂/d_w2=2*81.49*10³/291=560H

где d₂ - делительный диаметр колеса, мм.

Радиальная сила: F_r1=-F_r2 = F_t1tgα/cosβ=560*0.364/0.968=210H

где α=20° - угол в зацеплении.

Осевая сила: F_al = -F_a2 = F_t1tgβ = 560*0.26 = 146H