МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ

Брянский государственный технический университет

Кафедра «Промышленная электроника и электротехника»

Курсовая работа

по ТОЭ

Выполнил студент

группы 11-ЭиЭ :

Комяжко Е.А.

Проверил: Потапов Л.А.

БРЯНСК 2013

Часть 1

Задание

1. Выбрать схему цепи, в соответствии с номером по списку и для нее рассчитать классическим методом токи i₁(t) и i₂(t) после поочередного включения рубильников.

2. Найти i₂(t) операторным методом, пользуясь найденными в п.1 начальными условиями.

3. Построить график зависимости i₁(t), учитывающий все коммутации.

4. Используя программу Workbench, смоделировать заданные цепи и переходные процессы в них.

5. Для схемы, получившейся после замыкания всех ключей, выполнить расчет токов в установившемся режиме, если на входе цепи задано несинусоидальное напряжение амплитудой 311 В(получившееся после однополупериодного выпрямления).

6. Рассчитать и построить графики токов во всех ветвях.

7. Используя программу Workbench, смоделировать заданные цепи и получить осциллограммы токов во всех ветвях схемы.

Начальные данные и условия

Схема варианта № 8

Рис.1

Е=100 В (источник постоянной ЭДС), L=125 мГн, R2=50 Ом, R3=50 Ом, С=130 мкФ.

Рубильники включаются последовательно в соответствии с указанными на схеме номерами через τ секунд.

При возникновении колебательного процесса τ =Т₀/8, где Т₀ – период собственных колебаний.

При возникновении апериодического процесса τ =1/Р₁, где Р₁ – корень характеристического уравнения причем [P₁]<[P₂].

Выполнение:

1. Выбрать схему цепи, в соответствии с номером по списку и для нее рассчитать классическим методом токи i1(t) и i2(t) после поочередного включения рубильников.

Замыкание 1-го ключа(1-ая коммутация) (Подключение цепи RLC под постоянное напряжение)

рис.1

Дифференциальные уравнения цепи, получившейся после 1- ой коммутации, имеет вид:i₁R₃+L +U_c=E учитывая, что

Начальные условия: u_C (0₊) = 0, i₁(0₊) = 0

Составим характеристическое уравнение:

Z(p)=R3+pL+1/pC=0

где , , .

Мы получили два комплексных корня (т.к. ( ). Следовательно, в цепи происходят затухающие колебания.

Найдем частное решение неоднородного уравнения (принужденную составляющую). Частное решение определяют для установившегося режима(когда производная станет равна нулю), получим:

u_Cпр = E

Найдем общее решение однородрого ДУ (свободную составляющую). Общее решение ( когда правая часть ДУ равна нулю) представляет собой следующее выражение:

( т.к. в нашем случае корни получились комплексными).

Окончательно получаем:

Запишем выражение для тока:

Определим постоянную интегрирования (А) и ψ, путем совместного решения уравнений, предварительно подставив в них значения искомых величин при , т.е. сразу после коммутации (н.у.). Получаем:

Решив систему, находим , ; итак:

Итог – ток первой коммутации равен:

Замыкание 2-го ключа(2-ая коммутация) (Подключение цепи RC под постоянное напряжение)

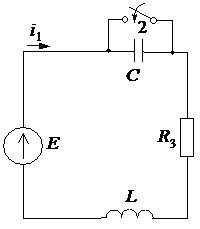
рис.2

Определим время замыкания 2- го ключа:

Дифференциальное уравнение цепи, получившейся после 2- ой коммутации, имеет вид:

, учитывая, что

Определим независимые начальные условия:

1.297 А

Найдем корни характеристического уравнения

Z(p)=R3+pL=0

p=-400

Находим принужденную составляющую тока i_1пр;

i_1пр=E/R3=2

Определим i₁(t)

i₁(t)=2+Ae^-pt

При 1.297=2+ ; A= - 0.703

В итоге

Замыкание 3- го ключа (3-ая коммутация)

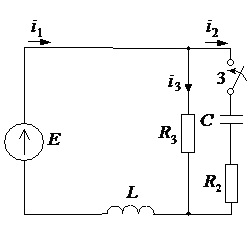
рис. 3

Определим время замыкания 3-го ключа:

Найдем независимые начальные условия, подставив в уравнение тока

А

Составим систему ДУ по законам Кирхгофа для получившейся цепи:

Перепишем систему уравнений данной цепи для установившегося режима (приравняв все производные к нулю):

Решив данную систему, мы найдем значения всех

принужденных составляющих:

;

Составим характеристическое уравнение и найдем его корни:

;

(корни комплексные, следовательно, в цепи происходит колебательный процесс).

Общий вид решения для тока : (с учетом, что ) (17)

Общий вид решения для тока : (с учетом, что )

(18)

С помощью системы уравнений найдем неизвестные начальные условия (зависимые значения токов и )

A.

Найдем начальные значения производных от токов:

451,8 А/с

Продифференцировав ур-е , и подставив в него , получим:

→ ,

итак А/с

Итак, . Неизвестные и определим из следующей системы уравнений:

i₁(t) =

Решим данную систему для времени :

Получим

Итог – ток третьей коммутации:

i₁(t)=

Итак, . Неизвестные и определим из следующей системы уравнений:

i₂(t) =

Решим данную систему для времени :

Получим

Итог – ток третьей коммутации:

i₂(t)=