Сдвиг фаз между током и напряжением. Понятие двухполюсника

Рассмотрим электрическую цепь состоящую из последовательно включенных сопротивления r, индуктивности L и емкости C (рис. 1 а)).

Протекающий ток i создает на всех элементах цепи падения напряжения, сумма которых равна напряжению на входе u. Для синусоидальных функций времени это можно записать в виде выражения

.

(1)

Пусть ток в цепи равен i = I_msin(t+_i). Подставим это выражение в (1) и получим:

.

(2)

Очевидно, что определить из выражения (2) амплитуду и начальную фазу напряжения u сложно. Поэтому перейдем в выражении (1) от оригиналов величин к их символическим изображениям комплексными числами или векторами.

.

(3)

Формально выражение (3) совпадает с записью закона Ома для цепи постоянного тока. Отличие заключается в том, что все величины входящие в него являются комплексными числами изображающими реальные функции времени. Поэтому его можно назвать законом Ома в области изображений.

Графически выражение (3) можно представить векторной диаграммой рис. 1 б). Здесь вектор входного напряжения U складывается из трех составляющих. Вектор падения напряжения на резистивном сопротивлении rI совпадает по направлению с током I , т.к. отличается от него только вещественным коэффициентом r . Вторая составляющая jx_LI перпендикулярна вектору тока I и опережает его по фазе на 90. Это связано с умножением на оператор поворота j вектора x_LI , совпадающего по направлению с током. Третий вектор jx_СI отстает по фазе от тока на 90 , т.к. образуется из него умножением на оператор поворота j .

Величина Z = r+j(x_L x_C) = r+jx = Ze ^jв выражении (3), имеющая размерность сопротивления, называется комплексным сопротивлением. Его вещественная часть r называется резистивным сопротивлением, а мнимая x = x_L x_C - реактивным сопротивлением. Из выражения (3) следует, что комплексное сопротивление является отношением комплексного падения напряжения к комплексному току

,

(4)

поэтому его модуль Z можно определить через отношение модулей напряжения и тока Z=U/I или через резистивную и реактивную составляющую . Модуль комплексного сопротивления называется полным сопротивлением.

Аргумент комплексного сопротивления  есть разность начальных фаз напряжения и тока, но его можно также определить по вещественной и мнимой составляющим комплексного сопротивления как  = arctg(X/R). Следовательно, сдвиг фаз между напряжением и током определяется только параметрами нагрузки и не зависит от параметров тока и напряжения в цепи. Из выражения (4) необходимо следует, что положительные значения  соответствуют отставанию тока по фазе, а отрицательные - опережению.

Таким образом, изображение напряжения на входе цепи можно представить через комплексное сопротивление в виде

.

(5)

Теперь можно вернуться к определению оригинала напряжения u на входе цепи рис. 1 а) преобразованием изображения (5) -

.

(6)

Из выражения (3) можно представить комплексное сопротивление суммой трех величин в виде

Z=r+jxL jxC=Zr+ZL+ZC

(7)

и изобразить эти соотношения на векторной диаграмме (рис. 1 в)). Векторная диаграмма сопротивлений подобна векторной диаграмме напряжений, т.к. комплексное сопротивление Z аналитически можно получить делением комплексного напряжения U на комплексный ток I . Графически это соответствует повороту векторной диаграммы напряжений на угол  _i и изменению ее масштаба на 1/I.

Соотношение между напряжением и током в электрической цепи можно выразить также величиной обратной сопротивлению

.

(8)

Величина Y называется комплексной проводимостью. Ее модуль является величиной обратной модулю комплексного сопротивления, а аргумент всегда равен его аргументу, но имеет противоположный знак.

Вещественная составляющая комплексной проводимости называется резистивной проводимостью, а мнимая - реактивной проводимостью.

Между резистивными (R и G) и реактивными (X и B)составляющими комплексной проводимости и сопротивления существует очевидное соответствие, вытекающее из понятия комплексного числа.

.

(9)

Отсюда следует:

• резистивные и реактивные составляющие комплексного сопротивления и проводимости в общем случае не являются взаимно обратными величинами;

• резистивные и реактивные составляющие комплексного сопротивления и проводимости являются взаимно обратными величинами только в случае отсутствия второй составляющей;

• реактивные составляющие комплексного сопротивления и проводимости всегда противоположного знака.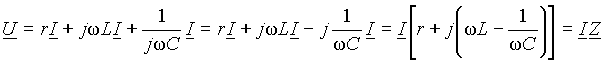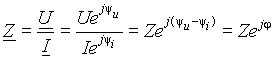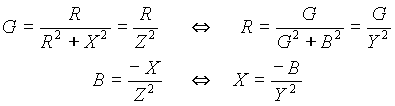