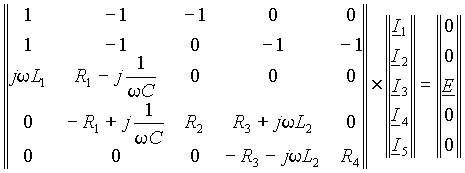Символический метод расчета
Анализ электромагнитных процессов в электрических цепях переменного тока в общем случае возможен только с использованием представления токов, напряжений и параметров цепи комплексными числами. Это позволяет исключить тригонометрические функции из уравнений, описывающих электрическую цепь и сделать их линейными. Так как при этом все величины заменяются их изображениями или символами, то этот метод носит название символического.
Последовательность операций в символическом методе в общем случае следующая:
преобразование всех величин и параметров электрической цепи в их изображения комплексными числами;
преобразование исходной электрической цепи в символическую схему замещения, где все величины и параметры представлены изображениями;
эквивалентные преобразования схемы замещения (если требуется);
определение искомых величин в области изображений;
преобразование искомых величин в оригиналы (если требуется).
Последняя операция не является обязательной, т.к. некоторые величины (амплитудные и действующие значения токов и напряжений, активные и реактивные составляющие и т.п.) не изменяются при обратном преобразовании.
Рассмотрим применение этого метода на примере цепи, изображенной на рис. 1 а).
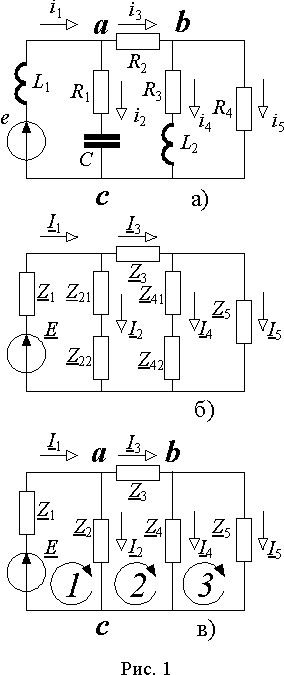Обозначим
стрелками направления токов принятые
за положительные. Тогда во временной
области для этой цепи можно составить
уравнения Кирхгофа в виде
|
(1) |
Если в выражениях (1) заменить токи и ЭДС синусоидальными функциями времени, то решить эту систему уравнений будет весьма затруднительно.
Перейдем к изображениям параметров исходной схемы комплексными числами в виде: Z1 = j L1; Z21 = R1; Z22 = j/( C); Z3 = R2; Z41 = R3; Z42 = j L2; Z1 = R4 . Этим параметрам соответствует схема замещения рис. 1 б). Вторая и четвертая ветви этой схемы имеют по два элемента. Их можно преобразовать как последовательное соединение к виду Z2 = R1 j/( C) и Z4 = R3+j L2, но соединения R1-C и R3-L2 можно сразу представить одним комплексным числом, в котором вещественная часть соответствует резистивному сопротивлению, а реактивная - емкостному и индуктивному. В результате схема замещения будет такой, как показано на рис. 1 в).
Переход от оригиналов к изображениям является линейной операцией, поэтому все законы справедливые для области оригиналов будут справедливы и для изображений. Кроме того, в области изображений отсутствует параметр времени и все величины являются константами, аналогично цепям постоянного тока. Поэтому формально в расчетах по схеме замещения можно применять не только основные законы электрических цепей, такие как законы Ома и Кирхгофа, но и все производные от них методы, т.е. метод контурных токов, узловых потенциалов, наложения, эквивалентного генератора и др.
Для символической схемы замещения можно составить уравнения Кирхгофа в виде
|
(2) |
Из этой системы уравнений можно найти, например, токи, представив ее в удобной для машинного анализа матричной форме записи
|
(3) |
или в развернутой форме
|
(4) |
Отсюда можно найти комплексные токи во всех ветвях, если известны параметры цепи и ЭДС источника. Пусть, например, e = 100sin(1000t-27 ) В; R1 = 20 Ом; R2 = 15 Ом; R3 = 30 Ом; R4 = 25 Ом; L1 = 10 мГн; L2 = 50 мГн; C = 50 мкФ. Тогда комплексные сопротивления и ЭДС будут Z1 = j10 Ом; Z2 = 20 j20 Ом; Z3 = 15 Ом; Z4 = 30+j50 Ом; Z5 = 25 Ом; Em = 100e j27 .
После решения системы
уравнений (2) получим: I1m
= 5.96e j40.4
А; I2m
= 3.67e j16
А; I3m
= 3.03e j70.5
А; I4m
= 1.02e j112.7
А; I5m
= 2.38e j53.7
А. В этих выражениях
определены амплитуды и начальные фазы
всех токов. Делением модулей токов на
можно
найти их действующие значения, а если
требуется, то можно представить и
синусоидальными функциями времени в
виде: i1 = 4.67sin(1000t
67.4
) А; i2 = 2.87sin(1000t
43
) А; i3 = 2.37sin(1000t
97
) А; i4 = 0.8sin(1000t
139
) А; i5 = 1.86sin(1000t
80
) А.
Найдем
теперь падение напряжения между узлами
a и c
цепи рис. 1 а), пользуясь эквивалентными
преобразованиями и законом Ома. Схема
замещения этой цепи приведена на рис.
1 в) и 2 а). Поэтапно
преобразуя цепь Z4
Z5
Z45= Z4
Z5/( Z4+
Z5)=18.7+j5.65 Ом;
Z45
Z3
Z345= Z45+
Z3=33.7+j5.65 Ом;
Z345
Z2
Z2345= Z345
Z2/( Z345+
Z2)=16.3 j6.1
Ом (рис. 2
б)-г)), перейдем к цепи, представляющей
собой один контур с последовательным
соединением Z1-Z2345-E.
Ток в контуре рис. 2 г) равен I1m = Em/(Z1+Z2345)=100e j27/(16.3+j3.9) = 5.96e j40.4 А. Как и следовало ожидать, ток I1m получился равным току рассчитанному по законам Кирхгофа. Отсюда искомая разность потенциалов Uacm= I1m Z2345=103.8e j61 или в области оригиналов uac = 103.8sin(1000t 61 ) В.
Следует обратить внимание на то, что в исследуемой цепи амплитуда падения напряжения между узлами a и c превышает амплитуду источника ЭДС. Объяснение этому явлению дано в анализе внешних характеристик источников питания переменного тока.
Трехфазные цепи
1. Основные определения
2. Соединение в звезду. Схема, определения
3. Соединение в треугольник. Схема, определения
4. Расчет трехфазной цепи, соединенной звездой
5. Мощность в трехфазных цепях
Основные определения
Трехфазная цепь является совокупностью трех электрических цепей, в которых действуют синусоидальные ЭДС одинаковой частоты, сдвинутые относительно друг друга по фазе на 120o, создаваемые общим источником. Участок трехфазной системы, по которому протекает одинаковый ток, называется фазой.
Трехфазная цепь состоит из трехфазного генератора, соединительных проводов и приемников или нагрузки, которые могут быть однофазными или трехфазными.
Трехфазный генератор представляет собой синхронную машину. На статоре генератора размещена обмотка, состоящая из трех частей или фаз, пространственно смещенных относительно друг друга на 120o. В фазах генератора индуктируется симметричная трехфазная система ЭДС, в которой электродвижущие силы одинаковы по амплитуде и различаются по фазе на 120o. Запишем мгновенные значения и комплексы действующих значений ЭДС.
Сумма электродвижущих сил симметричной трехфазной системы в любой момент времени равна нулю.
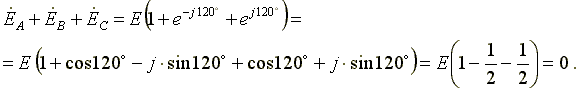
Соответственно
На схемах трехфазных цепей начала фаз обозначают первыми буквами латинского алфавита ( А, В, С ), а концы - последними буквами ( X, Y, Z ). Направления ЭДС указывают от конца фазы обмотки генератора к ее началу. Каждая фаза нагрузки соединяется с фазой генератора двумя проводами: прямым и обратным. Получается несвязанная трехфазная система, в которой имеется шесть соединительных проводов. Чтобы уменьшить количество соединительных проводов, используют трехфазные цепи, соединенные звездой или треугольником.