3.1.3. Графический метод определения оценок параметров распределения

Оценка параметров распределения производится по опытным данным. По ним же определяется, какому закону распределения соответствуют эти данные.

Можно было бы поступить следующим образом: нанести на график F(t) в прямоугольных координатах с равномерными шкалами значения этих величин, полученные из наблюдений, соединить точки F(t) плавной кривой и определить визуально, какому распределению это соответствует, сравнив с известными графиками. Однако кривые F(t) для разных законов распределения в ряде случаев похожи друг на друга и при таком методе может быть допущена грубая ошибка.

Оказывается, что путем несложных преобразований функцию F(t) можно в той же системе координат с неравномерными шкалами представить в виде прямой линии. В этом случае визуальное сравнение эмпирических данных с предполагаемым теоретическим значением может быть сделано с достаточной для практики точностью. Прямоугольная координатная сетка с измененным масштабом по осям носит название вероятностной сетки или вероятностной бумаги.

Для определения вида закона распределения случайной величины удобно представить данные наблюдений в графическом виде. Для графического представления данных наблюдения используется специальный график – гистограмма (рис. 16).

Рис. 16. Гистограмма и полигон распределения

3.1.4. Проверка согласия опытного распределения с теоретическим

Если графический и аналитический анализы результатов испытаний были проведены из предположения, что отказы распределяются по закону Вейбулла, то такое предположение о виде закона распределения называется статистической гипотезой.

Это предположение было обосновано визуальным сравнением, проведенным с помощью вероятностной сетки. При этом не произошло полного совпадения экспериментальных точек с соответствующими точками теоретической прямой.

Объясняются ли отклонения эмпирических данных от теоретических случайным рассеиванием или неправильным выбором закона, т.е. неверным построением гипотезы?

Для определения правильности выбранной гипотезы применяются критерии согласия.

Обычно в практике используются критерии согласия Колмогорова или Пирсона (критерий χ² - хи-квадрат), широко используемые при анализе надежности.

Для проверки по этому критерию необходимо подсчитать

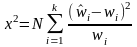, (25)

где - частости, полученные из опыта, w_i - частости, подсчитанные по формуле найденного теоретического распределения, N - число испытанных изделий.

Следует иметь в виду, что число наблюдений в каждом интервале должно быть не меньше 5. Так как обычно малочисленными бывают крайние интервалы, то их следует объединить, равно как и соответствующие им теоретические частости, которые могут быть подсчитаны путем умножения плотности вероятности отказа на длину интервала.

Полученную величину χ² надо сравнить с табличной. При этом надо предварительно подсчитать так называемое число степеней свободы

r = k-(s+1) (26)

где k - число интервалов; s - число параметров распределения.

Схема применения критерия χ² сводится к следующему:

• на основе опытных данных выбрать закон распределения изучаемого признака и найти его параметры;

• определить теоретические и эмпирические частости. Если среди опытных частостей имеются малочисленные, их необходимо объединить с соседними так, чтобы суммарный вес n_i, был не менее 5;

• вычислить величину χ². Определить число степеней свободы r;

• по полученным значениям χ² и r найти вероятность Р(χ²) из соответствующих таблиц;

• сформулировать вывод. Если вероятность окажется больше 0,01, то следует считать несущественными имеющиеся расхождения между теоретическими и опытными частостями, опытное распределение согласующимися с теоретическими. В противном случае, т.е. если Р(χ²) ≤ 0,01, то указанные расхождения признаются неслучайными, а избранный закон распределения отвергается.