Задача № 3

Для оценки качества поступившей партии товара произведено 5-процентное выборочное обследование. На основе механического бесповторного отбора проб получены следующие данные о содержании влаги:

Процент влажности	до 6	6 – 8	8 – 10	10 – 12	12 – 14	14 и более	Итого
Число проб	5	25	32	19	13	6	100

При условии, что к стандартной относится продукция с влажностью до 14 %, определите для всей партии товара:

1. С вероятностью 0,997 возможные пределы доли нестандартной продукции.

2. С вероятностью 0,954 возможные пределы среднего процента влажности.

Сделайте выводы.

Решение

1. Определим средний процент влажности, для этого построим таблицу (таблица 3)

Таблица 3. Таблица для расчета средней влажности

Влажность % (x)	Число проб (f)	(средняя арифметическая)	f влажность	- Отклонение от средней влажности	( - )	( - ) *f
6	5	6	30	-3,6	21,16	105,8
6–8	25	7	175	-2,6	6,76	169,0
8–10	32	9	288	-0,6	0,36	11,52
10–12	19	11	209	1,4	1,96	37,24
12–14	13	13	169	3,4	11,56	150,28
14 и более	6	14	84	4,4	19,36	116,16
Итого	100	-	955	-	-	590,0

1) 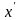= 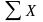/N – средняя арифметическая,

например: = 6+8/2 = 7

= 8+10/2 = 9 и т.д.

2) средний процент влажности определим по формуле

= ∑x’*f/∑f

= 955/100 = 9,6%

Определим дисперсию и среднее квадратическое отклонение по формулам:

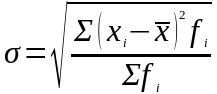среднее квадратическое отклонение

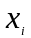• – значения изучаемого признака (варианты);

• – объем статистической совокупности;

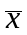• – средняя арифметическая величина.

= 590,0/100 = 5,9% – дисперсия

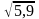= 2,43 – среднее квадратическое отклонение

3) V = /

*100% – коэффициент вариации

V = 2,43/9,6 = 25,3%

Вывод: данная совокупность считается однородной, т. к. коэффициент вариации составляет 25,3%, что меньше 33%.

3) Определим с вероятностью 0,954 возможные пределы значения влажности продукции для всей партии товара.

Сначала определим численность генеральной совокупности:

По условию задачи выборочная совокупность ( ) составляет 100 единиц проб, что составляет 5% генеральной совокупности (N), составим пропорцию:

100 ед. проб -5%

N – 100%

N = 100*100/5 = 2 000 ед. проб.

= 9,6% – средний % влажности в выборочной совокупности

_{= 5,9%}

t = 2 – коэффициент доверия, соответствует 0,954

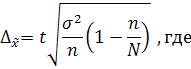
– коэффициент доверия;

– дисперсия количественно варьирующего признака выборочной совокупности;

– численность выборки;

– численность единиц генеральной совокупности.

▲ = 2*√5,9/100*(1–100/2000) = 2√0,059*(1–0,05) = 2√0,0056= 2*(-+0,24) =-+ 0,48%

Полученные значения и ▲X подставим в формулу предельного выбора для количественных признаков:

= +▲X

= 9,6% -+0,48

Вывод: с вероятностью 0,954 можно утверждать, что средний % влажности в генеральной совокупности (во всей партии) будет заключаться в пределах от 9,12 до 10,08

4) С вероятностью 0,997 которой соответствует коэффициент доверия 3, необходимо определить возможный % нестандартной продукции во всей партии, если известно, что из 100 проб, попавших в выборку 6 ед. отнесены к некачественной продукции (так как у 6 проб процент влажности 14 и более).

Итак, запишем, что дано:

m = 6 ед. – отнесены к нестандартной продукции;

n = 100 ед. – численность выборочной совокупности;

N = 2000 ед. численность генеральной совокупности;

t = 3 – коэффициент доверия

Определим

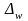
Так как необходимо определить пределы доли качественного признака используем формулу: Р = w -+

Генеральная доля равна выборочной доли -+ предельная ошибка выборки

w = m /n – выборочная доля

w = 6/100 = 0,06

Если коэффициент умножить на 100%, то получим 6%, т.е. в выборочной совокупности количество проб соответствующее нестандартной продукции составляет 6%.

По формуле предельной ошибки определим её значение:

=t *√ w (1‑w)/n * (1‑n/N)

= 3* √0,06*(1–0,06)/100 = 0,23*3 = 0, 069%

Полученные значения w подставим в формулу Р = w -+

Р = 0,06 -+ 0,069 или результат выразим в %: 6% -+0,69%

Следовательно с вероятностью 0,997 возможный процент нестандартной продукции во всей партии будет составлять от 5,31% до 6,69%.