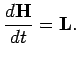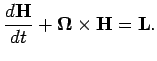- •1.Класифікація методів електророзвідки на постійному струмі.
- •2. Кількісна характеристика локальних гравітаційних аномалій для тіл правильної геометричної форми.
- •Кількісна інтерпретація гравіметричних даних.
- •3. Гамма-гамма метод ( густинний варіант – ггм-г).
- •1. Варіації магнітного поля. Їх природа та методика врахування при магнітних зйомках.
- •2. Блок – схема радіометрів. Радіометри для інтегральних вимірювань радіоактивності.
- •3. Годографи головних та відбитих хвиль , їх порівняльна характеристика.
- •1. Густина, сила тяжіння і тиск в надрах Землі.
- •2. Метод вертикального електричного зондування, його загальна характеристика та область застосування.
- •3. Обгрунтування вибору типового комплексу гдс для нафтогазових свердловин
- •1. Аналітичне продовження гравітаційних аномалій як один із способів іх трансформації.
- •2. Аерогамма-зйомка. Пішохідний гамма-метод.
- •3. Способи інтерпретації кривих електричного зондування
- •1. Фігура і гравітаційне поле Землі.
- •2. Вертикальне сейсмічне профілювання (всп)
- •3.Детектори радыоактивних випромынювань. Газонаповнены, сцинтиляцыйны, та напыв провыдниковы.
- •1. Застосування методів ядерної геофізики при вирішенні задач пошуків рудних родовищ корисних копалин
- •2. Магнітне поле Землі і його елементи. Природа магнітного поля
- •3. Методи вивчення технічного стану свердловин. Основні задачі що вирішуються цими методами.
- •1. Роль фізико-геологічного моделювання при комплексних геофізичних дослідженнях.
- •Моделі внутрішньої будови Землі за сейсмологічними даними. Сейсмическая модель Земли
- •Методи аналізу і розділення аномальних магнітних полів.
- •Гравітаційне поле Землі, його основні параметри та властивості.
- •Параметри пористості та насичення, їх фізична та петрофізична сутність.
- •Метод спільної глибинної точки (сгт).
- •1. Радіометричні методи при пошуках, розвідці та розробці родовищ радіоактивних руд і вирішенні інших геологічних задач.
- •2. Повздовжні та поперечні хвилі і особливості їх розповсюдження.
- •3. Методи електричного профілювання.
- •1. Порівняльна характеристика методів кількісної інтерпретації магнітних аномалій
- •2. Принципи цифрової реєстрації сейсмічних коливань
- •3. Гамма-гамма метод та його застосування в геології
- •1. Взаємодія гамма-випромінювання з речовиною г/п
- •2. Сутність акустичного методу дослідження свердловин та задачі, які вирішуються за його даними.
- •3. Якісна геологічна інтерпретація гравітаційних аномалій
- •Магнетизм та електропровідність Землі
- •Годографи відбитих та рефрагованих хвиль у градієнтних середовищах
- •Метод природного електричного поля
- •1. Прецесія та нутація осі обертання Землі. Припливний потенціал
- •2. Сучасні методи інтерпретації гравітаційних даних
- •Кількісна інтерпретація гравіметричних даних.
- •3.Особливості умов вимірів при гдс та їх вплив на вибір раціонального комплексу методів.
- •Стационарные нейтронные методы гис
- •2. Основні принципи комплексування геофізичних і геологічних методів дослідження
- •3. Багатохвильова сейсморозвідка
- •1. Магнітні властивості гірських порід і методи їх визначення
- •2. Статичні та кінематичні поправки в сейсорозвідці
- •3. Метод потенціалів викликаної поляризації гірських порід (вп)
- •1.Частотное электромагнитное зондирование.
- •2. Основи геотермії. Основні процеси утворення та переносу тепла в надрах Землі
- •3. Пряма та обернена задачі гравірозвідки, їх особливості
- •Магнітні властивості гірських порід і методи їх визначення
- •2. Принцип Гюйгенса–Френеля, принцип Ферма
- •3. Метод магнітотелуричного зондування
- •1. Намагнічування тіл в магнітному полі і характеристика намагнічування.
- •2. Бокове каротажне зондування (бкз) та боковий каротаж бк. Суть, призначення
- •3. Комплекс геофізичних досліджень при пошуках нафтогазових об’єктів
- •1.Термометрія свердловин та задачі,які нею вирішуються
- •1. Методи телуричних струмів та магнітотелуричного профілювання.
- •2. Розв’язання прямих і обернених задач в магніторозвідці для тіл простої геометричної форми
- •1. Методика магнітометричних досліджень при вирешенні геологічних задач на суші і на морі
- •2. Основні теорії походження Сонячної системи і Землі
- •3. Методи високочастотної електрометрії
- •1. Фотонейтронний (гамма-нейтронний) метод в ядерній геофізиці
- •2. Застосування методу осереднення при аналізі гравімагнітних спостережень
- •3. Застосування 3d сейсморозвідки для вирішення геологічних задач
- •1.Функція комплексного показника та її використання при геофізичних дослідженнях.
- •2. Методика та апаратура магнітотелуричних досліджень.
- •10.Методика польових магнітометричних досліджень.
- •3. Теорія методу самочинної поляризації гірських порід (пс). Методика та область застосування. Задачі, що вирішуються методом пс.
1. Прецесія та нутація осі обертання Землі. Припливний потенціал
В
основе теории вращения Земли лежит
закон сохранения углового момента
системы, который гласит, что угловой
момент замкнутой системы при равенстве
момента внешних сил нулю сохраняется.
Если
![]() -
вектор углового момента,
-
вектор углового момента,
![]() -
момент внешних сил, то в инерциальной
системе отсчета уравнение вращательного
движения тела имеет вид:
-
момент внешних сил, то в инерциальной
системе отсчета уравнение вращательного
движения тела имеет вид:
|
(7.1) |
Если
![]() ,
то из (7.1)
следует, что
,
то из (7.1)
следует, что
![]() .
.
Если
на Землю действуют внешние силы, момент
которых не равен нулю, то под их действием
происходит изменение ориентации вектора
углового момента Земли. По определению
вектор углового момента равняется
произведению тензора инерции
![]() на
вектор угловой скорости вращения Земли
на
вектор угловой скорости вращения Земли
![]() :
:
|
(7.2) |
Если
![]() ,
то из (7.1)
и (7.2)
следует, что векторы
и
будут
изменять свое положение в инерциальной
системе отсчета.
,
то из (7.1)
и (7.2)
следует, что векторы
и
будут
изменять свое положение в инерциальной
системе отсчета.
Под внешними силами в данной главе мы будем понимать силы притяжения Земли Луной и Солнцем7.1. В этом случае смещение вектора углового момента Земли в пространстве называется лунно-солнечной прецессией. Так как силы притяжения и их момент меняются во времени из-за обращения Земли вокруг Солнца и Луны, то это приводит к периодическим движениям вектора углового момента Земли, которые накладываются на медленное прецессионное движение и называются нутацией.
Во вращающейся системе координат уравнение (7.1) имеет вид:
|
(7.3) |
Уравнение (7.3) используется для определения влияния геофизических процессов, таких как перемещение масс в атмосфере и океанах, тектоническое движение плит коры Земли, землетрясений и т.д., на вращение Земли и описывает движение вектора в земной системе координат. Эти процессы приводят к изменению тензора инерции Земли, влияя, следовательно, на вращение Земли. Если считать, что атмосфера и океаны связаны с Землей и составляют с Землей замкнутую систему, то . Это значит, что вектор углового момента под действием геофизических процессов сохраняет свое положение в пространстве. Но так как из-за перемещения масс происходит изменение тензора инерции Земли, то вектор изменяет свою ориентацию относительно вектора , т.е. вектор движется относительно самой Земли. Наблюдателю, находящемуся на поверхности Земли, кажется, что Земля качается относительно оси углового момента. Поэтому иногда это движение называется качанием Земли (по-английски "wobble"), но чаще движением полюса.
Нутация и движение полюса тесно связаны друг с другом, и о точном определении этих явлений будет рассказано позже при определении небесного эфемеридного полюса.
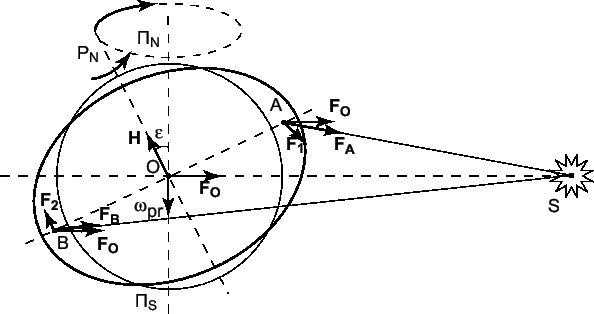
Причиной прецессии и нутации является несферичность Земли и несовпадение плоскостей экватора и эклиптики. В результате гравитационного притяжения Луной и Солнцем экваториального утолщения Земли возникает момент сил, стремящийся совместить плоскости экватора и эклиптики (рис. 7.2).
|
Рис. 7.2. Объяснение прецессии и нутации |
Как
будет показано ниже, лунно-солнечный
момент сил, вызывающий прецессию
пропорционален
![]() ,
где
,
где
![]() -
расстояние от Земли до Солнца или Луны.
Из-за близости Луны к Земле главную роль
в прецессионном и нутационном движении
полюса мира играет не Солнце, а Луна:
влияние Луны примерно в два раза больше.
-
расстояние от Земли до Солнца или Луны.
Из-за близости Луны к Земле главную роль
в прецессионном и нутационном движении
полюса мира играет не Солнце, а Луна:
влияние Луны примерно в два раза больше.
Из
рис. 7.2
видно, что так как
![]() ,
то
,
то
![]() и
из векторных равенств
и
из векторных равенств
![]() ,
,
![]() получим
получим
![]() .
.
Пара
сил
![]() и
и
![]() ,
следовательно, стремится повернуть
плоскость экватора
,
следовательно, стремится повернуть
плоскость экватора
![]() по
часовой стрелке. Из-за вращения Земли
такого поворота не происходит, но
ориентация оси вращения изменяется:
она описывает в пространстве конус, и
угол между осью вращения Земли и осью
по
часовой стрелке. Из-за вращения Земли
такого поворота не происходит, но
ориентация оси вращения изменяется:
она описывает в пространстве конус, и
угол между осью вращения Земли и осью
![]() равен
равен
![]() .
.
Приливний потенціал
Приливное
возмущение потенциала неизбежно
деформирует уровенную поверхность
планеты. Выполним приближенную оценку
этих искажений. Для простоты будем
считать, что Земля шар со сферически
симметрично распределенной массой.
Тогда ее невозмущенный гравитационный
потенциал на поверхности планеты имеет
простой вид
![]() .
Для точки
.
Для точки
![]() ,
находящейся на расстоянии
,
находящейся на расстоянии
![]() от
центра сферы гравитационный потенциал
Земли равен
от
центра сферы гравитационный потенциал
Земли равен
![]() .
Добавляя сюда приливной потенциал,
получим возмущенную поверхность уровня
.
Добавляя сюда приливной потенциал,
получим возмущенную поверхность уровня
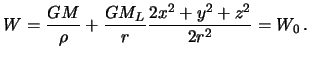
Итак,
уровенная поверхность, заданная в виде
шара, вследствие приливного действия
другого небесного тела вытягивается в
сторону этого тела и превращается в
эллипсоид вращения. Большая полуось
будет превышать радиус планеты на
величину
![]() ,
а малые полуоси будут меньше радиуса
на величину
,
а малые полуоси будут меньше радиуса
на величину
![]() .
Заметим, кстати, что с той же степенью
точности произведение всех трех полуосей
остаются постоянными, что говорит о
неизменности объема, ограниченного
поверхностью уровня.
.
Заметим, кстати, что с той же степенью
точности произведение всех трех полуосей
остаются постоянными, что говорит о
неизменности объема, ограниченного
поверхностью уровня.
Для
иллюстрации сказанного приведем
численный пример. Вычислим приливной
"горб" на Земле, вызванный притяжением
Луны. Радиус Земли равен
![]() =
6378 км, расстояние между центрами
Земли и Луны равно
=
6378 км, расстояние между центрами
Земли и Луны равно
![]() км,
отношение масс Луна/Земля равно 1:81.
Подставляя эти данные в формулу для
увеличения большой полуоси, получим
0,36 м Нетрудно подсчитать, что на
Луне аналогичный приливной горб,
направленный в сторону Земли будет
равен 13 м.
км,
отношение масс Луна/Земля равно 1:81.
Подставляя эти данные в формулу для
увеличения большой полуоси, получим
0,36 м Нетрудно подсчитать, что на
Луне аналогичный приливной горб,
направленный в сторону Земли будет
равен 13 м.
Необходимо подчеркнуть, что в приведенных рассуждениях не учитывается приливные деформации самой Земли, что также изменит поверхность уровня. Для строгих выкладок необходимо задать модель Земли, ее строение, упругие постоянные и т.п.,