1. Кількісна інтерпретація гравіметричних даних.

Інтерпретація отриманих в результаті гравіметричних робіт даних завершує дослідження відповідної території. Розгляду підлягають карти ізоаномал і профілі значень Δg, наявні геологічні дані, матеріали вивчення густини зразків гірських порід, результати інших геофізичних досліджень.

При інтерпретації повинні бути виділені гравітаційні аномалії, виявлена форма, об’єм, глибина й елементи залягання геологічних тіл, що збурюють поле, установлені зв'язки гравітаційного поля з особливостями геологічної будови досліджуваної території.

Інтерпретація даних гравірозвідки неоднозначна. Це пояснюється двома основними особливостями гравітаційного поля. Перша полягає в тому, що вимірюване значення сили тяжіння в будь-якому пункті відбиває вплив «накладених» один на одного багатьох неоднорідностей у розподілі мас. Успішно інтерпретувати гравітаційні аномалії можна тільки після поділу впливу окремих геологічних об'єктів, що особливо важливо при пошуках локальних структур. Друга особливість складається в принциповій невизначеності рішення зворотної задачі по полю сили тяжіння (як і для будь-якого іншого потенційного поля).

Геологічна інтерпретація гравірозвідувальних даних підрозділяється на два основних підетапи: якісна інтерпретація і кількісна інтерпретація.

Кількісно інтерпретуються параметри збурюючи поле тіл, їх маси і густини. Результатом інтерпретації є геолого-геофізичні розрізи визначених напрямків (інтерпретаційні профілі), структурні карти поверхонь розділу середовищ різної густини. Найбільше застосовується при кількісній інтерпретації аналітичний спосіб і спосіб підбору.

Аналітичний спосіб інтерпретації заснований на використанні формул для тіл правильної геометричної форми, якими апроксимуються реальні геологічні тіла. При цьому виконується оцінка параметрів тіл (глибини залягання, надлишкової маси й ін.) за характерними точками аномалій (максимуми, мінімуми, їхньої частки й ін.).

Інтерпретація зводиться до вирішення прямої і зворотної задач гравірозвідки. Пряма задача полягає в знаходженні елементів гравітаційного поля за заданим розподілом параметрів (формі, глибині залягання збурюючого тіла, його густині тощо). Вона має єдиний розв’язок. Для вирішення прямої задачі в теорії гравірозвідки розроблений спеціальний математичний апарат  інтегральні формули, що виражають похідні гравітаційного потенціалу як функції розподілу аномалієутворюючих мас. Практично це зводиться до підстановки меж інтегрування для заданого тіла. Найбільш проста для рішення при цьому двовимірна задача. В цьому випадку обчислюється розподіл похідних гравітаційного потенціалу по лінії, що перетинає проекцію аномалієутворюючого джерела на поверхню спостереження, що проходить через його центр і перпендикулярна простяганню тіла, об'єктам. Це горизонтальна матеріальна напівплощина, горизонтальний стрижень, циліндр, вертикальний уступ, похилий уступ, вертикальний пласт, похилий пласт, прямокутна нескінчена призма тощо. Набагато складніший процес рішення тривимірної задачі. Але для ряду правильних геометричних форм (матеріальна точка, сфера, вертикальний стрижень, круговий диск, вертикальний круговий циліндр, прямокутний паралелепіпед) відповідні аналітичні вирази отримані. Якщо суворе аналітичне вирішення задачі визначити дуже складно чи зовсім неможливо, пряму задачу вирішують приблизно, зображуючи отримані результати графічно у вигляді палеточних кривих. Так, зокрема, роблять, коли розглянутий аномалієутворюючий об'єкт не можна уподібнити тілу правильної геометричної форми.

Зворотна задача полягає у визначенні параметрів збурюючого тіла за відомим значенням поля аномалій сили тяжіння. Вона вирішується неоднозначно, тому що однакові аномалії сили тяжіння можуть бути зв'язані з геологічними об'єктами різної форми, розмірів, густини. Тому для підвищення вірогідності інтерпретації необхідні дані про густину порід, що складають даний район, а також ймовірній формі тіл, які досліджуються. Природно, що результати інтерпретації будуть тим достовірнішими, чим більш обґрунтовано вибрана модель досліджуваного поля. Методи вирішення зворотної задачі застосовують як для інтерпретації щодо простих аномалій, які можна апроксимувати тілами простої геометричної форми за допомогою аналітичних методів, зокрема методом характерних точок, так і при інтерпретації складних аномалій за допомогою палеток, методом послідовних наближень з використанням ЕОМ.

У методі характерних точок використовуються формули розрахунку аномалій Δg і других похідних гравітаційного потенціалу для тіл простої форми, отримані при рішенні прямих задач. Досліджуючи ці аналітичні вирази, визначають координати характерних точок відповідних похідних (звідси назва методу). Звичайно це точки максимуму і мінімуму, напівмаксимуму, нульових значень. Знаходять також значення аномалії в точках максимуму і мінімуму. Цей аналіз дозволяє для кожного тіла одержати систему рівнянь. З неї і визначають невідомі елементи залягання аномалієутворюючого тіла, тобто вирішують зворотну задачу. Так, для тіл сферичної форми значення сили тяжіння і її горизонтального градієнта по будь-якому профілю, що проходить через епіцентр тіла, визначають по формулах: 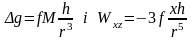, де М — надлишкова маса тіла; h - глибина залягання центра сфери; f — гравітаційна постійна; ; х — абсциса довільної точки на осі х (рис. 1.3).

Рисунок 1.3 Криві g і W над сферою (а) та вертикальним уступом (б)

Максимум кривої Δg знаходиться над центром кулі (х = 0) і дорівнює: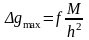 Для точки відстороненої від максимуму на відстань х_0,5, де 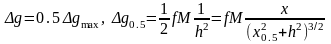чи . Звідси можна знайти глибину залягання центра сфери. Надлишкова маса буде дорівнювати: 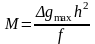. Параметри h і М визначають по кривій,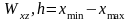 . Наведений приклад є дуже важливим в практиці геологічної інтерпретації гравірозвідувальних даних. Геологічні тіла, які можуть бути уподібнені сфері, дуже різноманітні: поклади гніздоподібної і штокоподібної форми, карстові форми, соляні купола і таке ін.

Друга, що дуже часто зустрічається в природі, форма – поверхня контакту. При картуванні контактної поверхні можна застосовувати спрощену формулу, засновану на припущенні, що спостережене гравітаційне поле обумовлене тільки дією цієї поверхні з надлишковою щільністю 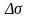. 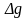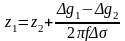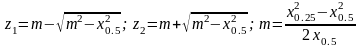Якщо відоме значення якій-небудь точці, де глибина залягання контактної поверхні z₂, то в будь-якій іншій точці , то глибину залягання верхньої і нижньої границь уступу і надлишкову щільність (m) можна оцінити по формулах , де 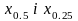- абсциси точок спостережень, у яких значення досягають 0,5 і 0,25 свого максимального значення. Сучасна кількісна інтерпретація  трудомісткий процес, як правило, вона виконується на основі використання обчислювальної техніки. Тим часом у практиці геологічних досліджень дуже часто важливо зробити орієнтовані розрахунки параметрів аномалієутворюючих тіл. З цією метою часто застосовують спрощені аналітичні вираження. 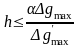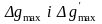До їхнього числа відноситься нерівність Сміта: , де = 0,7 для витягнутих і = 0,9 для ізометричних відповідно максимальне значення сили тяжіння максимальний горизонтальний градієнт; знімаються з інтерпретаційного графіка Δg, що проходить завжди поперек простягання інтерпретуючої аномалії через її центр.

У практиці рішення зворотної задачі крім розглянутих аналітичних способів застосовують і інші. Наприклад, використовують побудовані за формулами вирішення прямої задачі атласи теоретичних кривих. При їхній побудові по осі абсцис відкладається відношення горизонтальної координати до якого-небудь лінійного параметра по вертикалі (наприклад, до глибини залягання). Для багатьох тіл навіть правильної геометричної форми одержати аналітичне рішення прямої задачі, як уже вказувалося, важко. Однак його досить легко можна одержати з будь-якого заздалегідь заданим ступенем точності наближенням і відобразити у вигляді відповідних теоретичних кривих (палеток). Побудову палеток виконують по інтерпретаційному профілю для тіла визначеної форми, що має, однак, різні розміри, елементи залягання й інші параметри. Зіставлення експериментальної кривої з палеточними дозволяє підібрати теоретичну криву, найбільш близьку до тієї, що інтерпретується. Тим самим визначаються всі параметри аномалієутворюючого об'єкту, тобто зважується зворотна задача. Надійність її рішення легко визначити, знаючи ступінь співпадання інтерпретуючої кривої з палеточною.

Інтерпретація гравітаційних аномалій за аналітичними формулами і атласам теоретичних кривих, розрахованим для тіл правильної геометричної форми, часто дуже орієнтована. Для її уточнення широко застосовується спосіб підбору.

Спосіб підбору полягає у виборі такого тіла, форма, розміри, елементи залягання і густина якого дають розрахункову криву, що найбільше близько збігається зі спостереженою. Для цього широко використовуються ЕОМ. Крім того, для оцінки гравітаційного ефекту від тіл довільної форми використовуються спеціальні палетки.

Сутність побудови цих палеток у двовимірному варіанті зводиться до того, що вся площина нижче вихідної осі розбивається на елементарні площадки, що відзначаються рівною гравітаційною дією. За допомогою такої палетки будь-яке тіло може бути розбите на площадки, що робить на розрахункову точку однаковий гравітаційний вплив. Підрахувавши суму цих площадок і, помноживши їх на гравітаційний вплив однієї з них, одержимо гравітаційний вплив усього тіла. Очевидно, у такий спосіб можуть бути розраховані криві гравітаційних аномалій від будь-якої кількості тіл. Наведений підхід реалізується і при використанні комп’ютера для інтерпретації гравітаційного поля. При цьому робота інтерпретатора практично зводиться лише до підбору геологічного реального розташування геологічних тіл (петрогустинної моделі).