3. Планы и оперативные характеристики планов выборочного контроля

При приемке партии продукции контроль может быть сплошным, когда контролируется каждая единица продукции (например, подшипник, бутылка воды, моток провода и т.п.). Такой контроль чаще всего экономически необоснован, а иногда и невозможен. Более распространен выборочный контроль, когда заключение о качестве партии продукции делается на основе анализа выборки ограниченного объема.

Выборочный контроль подразделяется:

•по времени проведения: на входной (закупочный контроль сырья и полуфабрикатов), промежуточный (межоперационный) и выходной (приемка и сертификация готовой продукции);

•по изменениям в результате контроля: на разрушающий и неразрушающий (например, для контроля прочности изделия его необходимо довести до разрушения);

• по жесткости: на нормальный, усиленный (более сложный) и облегченный; переход с одного вида контроля на другой производится в зависимости от количества партий, которые были последовательно приняты, или наоборот, отклонены потребителем;

• по контролируемому параметру: на количественный (в этом случае производится измерение контролируемого показателя качества продукции) и качественный (в частности, наиболее распространен контроль по альтернативному признаку, когда о каждом контролируемом объекте делается заключение, годен он или негоден, соответствует предъявляемым требованиям или не соответствует),

Применение плана статистического контроля по существу является проверкой статистической гипотезы h₀. качество партии соответствует предъявляемым требованиям при альтернативной гипотезе Н₁ качество партии не соответствует предъявляемым требованиям.

Основной характеристикой партии изделий при контроле по альтернативному признаку является генеральная доля дефектных изделий (процент несоответствующих единиц продукции в совокупности или партии) р ~D/N,

где В— число дефектных изделий в партии объемом N

Как правило, в практике статистического контроля генеральная доля p неизвестна и ее следует оценивать по результатам контроля ряда случайных выборок объема n изделий, из которых d — дефектные.

Процент несоответствующих единиц продукции в выборке - это число несоответствующих единиц продукции в выборке, умноженное на сто и деленное на объем выборки, т.е.,

Р = (d/n) 100

где d- число несоответствующих единиц продукции в выборке;n - объем выборки 

Процент несоответствующих единиц продукции в совокупности или партии:

Число несоответствующих единиц продукции в совокупности или партии, умноженное на сто и деленное на объем совокупности или партии, т.е.

100p = 100D/N,

где p- доля несоответствующих единиц продукции;

D - число несоответствующих единиц продукции в совокупности или партии;

N - объем совокупности или объем партии.  

Термины "процент несоответствующих единиц продукции" и"процент несоответствий на 100 единиц продукции" используются главным образом вместо терминов "доля несоответствующих единиц продукции" и "процент несоответствий на единицу продукции", ранее широко применявшихся.

Процент несоответствий на 100 единиц продукции в выборке – это число несоответствий в выборке, умноженное на сто и деленное на объем выборки,.

, Р = 100d/n

где d- число несоответствий в выборке; n- объем выборки.

Процент несоответствий на 100 единиц продукции в совокупности или партии: Число несоответствий в совокупности или партии, умноженное на сто и деленное на объем совокупности или объем партии, т.е. 

, 100p = 100D/N,

где p- доля несоответствующих единиц продукции;

D - число несоответствующих единиц продукции в совокупности или партии;

N - объем совокупности или объем партии.

(Единица продукции может содержать одно или более несоответствие.)

Под планом статистического контроля будем понимать систему правил, указывающих методы отбора изделий для проверки, и условия, при которых партию следует принять, забраковать или продолжить контроль.

Различают следующие виды планов статистического контроля партии продукции по альтернативному признаку:

одноступенчатые,

двухступенчатые,

многоступенчатые

последовательные.

Одноступенчатые планы

Если среди n случайно отобранных изделий число дефектных от окажется не больше приемочного числа C (d < C), то партия принимается; в противном случае партия бракуется.

Двухступенчатые планы. Если среди n_l случайно отобранным изделий число дефектных m_t окажется не больше приемочного числи с, (m_i < Cj), то партия принимается; если m_t >.d_t, где d_t — браковочной число, то партия бракуется. Если же c_i<m_i< d_{, то принимается решение о взятии второй выборки объемом п₂. Тогда если суммарное число дефектных изделий в двух выборках (m₁, + т₂) < с₂, то партия принимается, в противном случае партия бракуется по данным двух выборок. На рисунке 1 приведена схема двухступенчатого плана контроля.

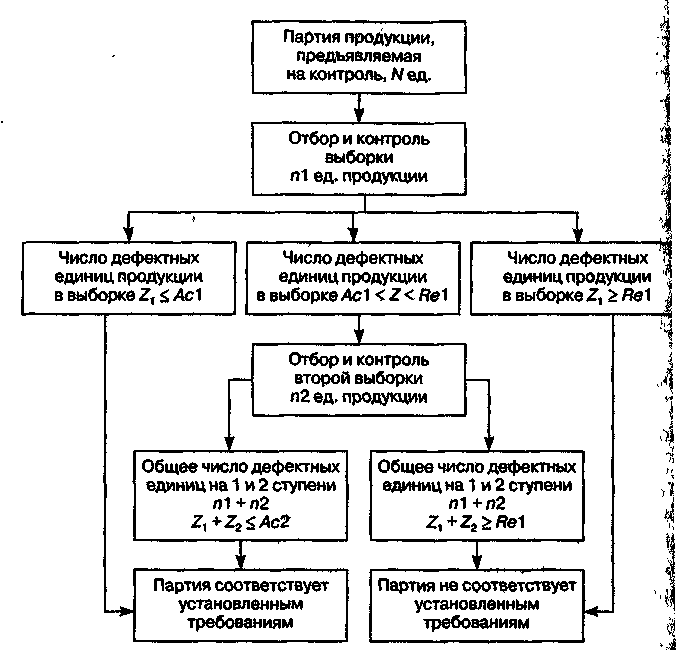
Рисунок 1. Схема двухступенчатого плана выборочного контроля

В случае контроля одиночных партий продукции выбор плана контроля целесообразно осуществлять на основе анализа оперативной характеристики с учетом браковочного уровня дефектности.

Многоступенчатые планы являются логическим продолжением двухступенчатых планов. Первоначально берется выборка объемом n и определяется число дефектных изделий m₁. Если т₁ < с то партия принимается. Если т₁, > d_i (di > c_t +1), то партия бракуется. Если жe C₁ < m < d_i то принимается решение о взятии второй выборки объемом п₂. Пусть среди n₁, + п₂ изделий имеется т₂ дефектных. Тогда если т₂ < с₂, где с₂ — второе приемочное число, то партия принимается; если m₂ > d₂ (d₂ > c₂ + 1), то партия бракуется. При с₂ < т₂ < d₂ принимается решение о взятии третьей выборки. В дальнейшем контроль проводится по аналогичной схеме, за исключением последнего k-ro шага, при котором если m_k < с_а, то партия принимается, если же m_k > c_k, то партия бракуется. При этом обычно принимается, что объем выборок одинаков.

Последовательные планы. Решение о контролируемой партии принимается после оценки качества ряда выборок, общее число которых заранее не установлено и определяется в процессе контроля по результатам предыдущих выборок

Одноступенчатые планы наиболее просты при организации контроля на производстве. Двухступенчатые, многоступенчатые и последовательные планы обеспечивают при том же объеме выборки большую точность принимаемых решений, но они более сложны в организации контроля и требуют значительных вычислений.

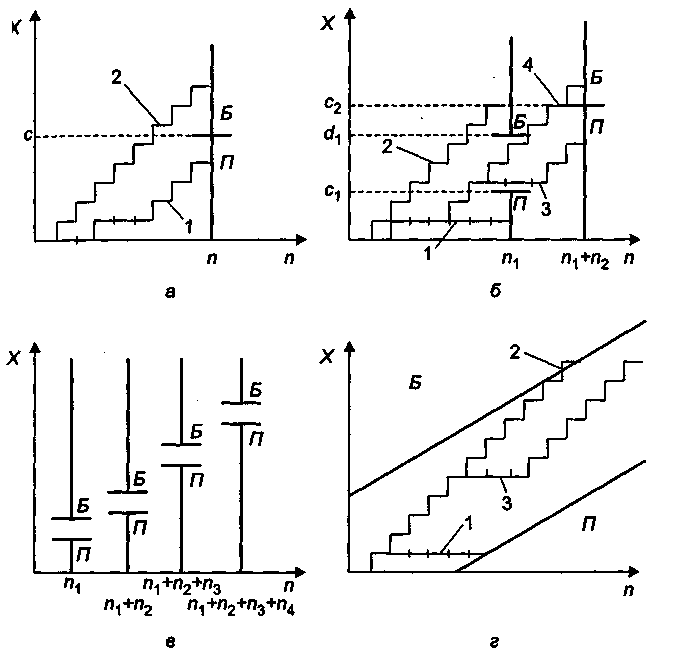
Рисунок.2. Графическое изображение планов контроля

:а — одноступенчатый (1 — приемка, 2 — браковка партии);

б - двухступенчатый (1 - приемка на первой ступени, 2 — браковка на первой ступени, 3 — приемка на второй ступени, 4 — браковка на второй ступени);

в — четырехступенчатый; г — последовательный контроль (1 - приемка, 2 - браковка,3 — продолжение контроля)

г- последовательный.

Задача статистического выборочного контроля фактически сводится к статистической проверке гипотезы о том, что доля дефектные изделий q в партии равна допустимой величине q₀. Задача правильного выбора плана статистического контроля состоит в том, чтобы сдёлать ошибки первого рода (риск поставщика) и второго рода (риск потребителя) маловероятными.

Основным вероятностным показателем плана статистического контроля является оперативная характеристика.

Оперативной характеристикой плана контроля называется функция P(q), равная вероятности принять партию продукции с долей дефектных изделий q. Очевидно, что для каждого плана будет своя оперативная характеристика. В случае сплошного контроля продукции, при котором дефект не может быть пропущен, оперативная характеристика будет идеальной.

Она соответствует следующей функции:

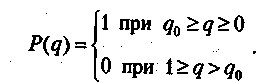
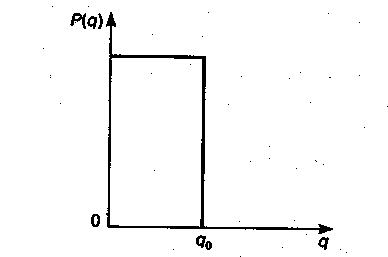
Рисунок 3 - Идеальная оперативная характеристика

Для планов выборочного контроля оперативная характеристика, приведенная на рис. 4, имеет вид плавной кривой.

Рисунок.4. Оперативная характеристика плана выборочного контроля: α — риск поставщика; β — риск заказчика; с — приемочное число

Каждый план имеет свою оперативную характеристику, которая демонстрирует его свойства. На горизонтальной оси указан уровень качества производственного процесса , на вертикальной оси – число партий в процентах, которые будут приняты при использовании этого плана. Оперативная характеристика может быть задана в виде таблицы, в виде формулы или в виде графика.

Пример . Построим оперативную характеристику плана приемочного контроля P(q) для разных долей дефектных изделий q (табл..1) при объеме партии N= 1200, объеме выборки п = 100, приемочном числе С = 3.

Решение

Оперативную. характеристику зададим в виде таблицы и в виде графика

.Таблица 1

q,%	0	1	2	3	4	5	6	7	8	9	10
P(q)	1.0	0.98	0.86	0.65	0.43	0.25	0.15	0.08	0.04	0.02	0.01

Вероятность приемки партии P(q) рассчитаем по формуле(используя гипергеометрический закон распределения числа дефектных изделий

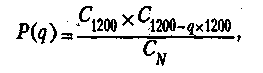
где c_n — число сочетаний из N элементов по .n

На рисунке показаны: - риск поставщика; - риск заказчика; AQL - приемочный уровень дефектности (accept - принимать; quality - качество; level - уровень); LQ - браковочный уровень дефектности. На кривой F(q) = f(q) совпадение заданных и в точке и LQ и в точке маловероятно, что и показано на рисунке. Другими словами кривая F(q)=f(q) должна быть согласована с величинами AQL, , LQ и .

Покажем процедуру использования оперативной характеристики плана приемочного контроля на численном примере.

Рассмотрим тенденции изменения вида функции F(q) при изменении величин n, Ac:

1. Допустим, что Ас / n = const, но n и Ас увеличиваются. Кривая при этом увеличивает свою крутизну и в пределе, когда n = N, выборочный контроль перейдет в сплошной и AQL = LQ.

2. Пусть при n = const, Ас увеличивается.

3. Если при n = const, Ас увеличивается, то контроль становится менее жестким.

4. Ас = const; n увеличивается, контроль ужесточается.

Для разных планов контроля кривые функции P(q) будут иметь различный вид. Для примера приведем в таблице.2 вероятности принятия партии Р(q), варьируя значениями параметров (n, с,q),а на рисунке..3 отразим оперативные характеристики Р(q) нескольких планов.

Из графика видно, что планы с C = 0 даже при малых значениях дефектности партии р гарантируют небольшую вероятность приемки партии, т.е. эти планы очень жесткие. •

Рисунок 5-. Оперативные характеристики:

а —план (5,0);

б —план (20,0);

в —план (20,2)

Таблица 2 -Вероятность приемки партии Р(q)

план (n,C);	Уровень дефектности, q
	0,05	0,1	0,3	0,5
(10,2)	0,99	0,93	0,38	0,05
(20,0)	0,36	0,12	0	0
(20,2)	0,92	0,68	0,4	0

В случаях, где единственно возможным методом контроля критических дефектов является разрушающий контроль (например, цельносварные изделия ракетной техники), можно проводить выборочный контроль.

В этом случае приемочное число A_c. = 0, а браковочное число R_c = 1. Объем выборки определяется по формуле n=k/p

Где k — коэффициент, зависящий от риска появления одной дефектной единицы продукции в выборке;

р — максимально допустимый процент дефектных единиц продукции в выборке