10. Модели принятия решения, с помощью которых можно оценить процесс преобразования входов в выходы или осуществить выбор вариантов.

Действия и решения в системе являются прерогативой ЛПР. Каждое решение должно направлять систему на достижение поставленных целей.

Существует два типа моделей принятия решений:

- модели преобразования, связывающие вход и выход системы;

- модели выбора, позволяющие выбрать наилучший вариант системы для достижения цели, из некоторого исходного множества вариантов.

В нашем случае используем модель второго типа - модель выбора, для чего составим сравнительную таблицу с учётом важности характеристик (критериев). В качестве модели выбора используем аддитивную свёртку.

Таб.1. Сравнительная таблица с учетом важности характеристик

Характеристики (критерии)	Марки стиральных машин (варианты)
	В1	В2	В3
	Samsung WF 0600NCY	Bosch WAS 24443 OE	LG F-1495 BDS
К1 - типы белья (все);	3	4	5
К2 - масса загрузки (до 8 кг);	3	4	5
К3 - Качество стирки (высокое);	3	5	5
К4 - режимы стирки (более 10);	3	5	5
К5 - габариты (средние);	4	5	4
К6 - энергозатраты	5	4	3
К7 - уровень шума (низкий);	4	5	5
К8 – стоимость (до 20 тыс.р.)	5	3	3

11. Тип системы.

Стиральная машина является физической, технической, искусственной неживой, статической, дискретной, относительно закрытой системой. По преобразовательным возможностям относится ко второму типу (изменяются отдельные характеристики).

12. Свойства системы. В чём они состоят?

Система "стиральная машина" является иерархически упорядоченной, так как состоит из подсистем.

Система централизована, так как центром является мотор, обеспечивающий работу (движение) остальных элементов.

Система является инерционной, так как имеет конечное время обработки.

Система адаптивна, так как сохраняет свои функции при возмущающих воздействиях среды, например, при изменении качества ухода и обслуживания, изменении погодных условий (температура, влажность, давление), и т.д.

13. Принятие решения.

При принятии решения о повышении качества выпускаемой системы – стиральная машина, фирме-производителю необходимо учитывать следующие внешние системы:

- потребителей, которые предъявляют определённые требования к качеству продукции;

- маркетинговую систему, так как сначала необходимо выяснить, какие именно требования предъявляют потребители;

- систему своих собственных внутрифирменных ресурсов (человеческих, материальных, финансовых);

- производственную систему, то есть производственные возможности и производственные мощности;

- систему поставщиков, от которых зависит качество сырья и комплектующих;

- технологическую систему, от которой зависит возможность улучшения качественных показателей и технология изготовления;

- экономическую систему, от которой зависят финансовые условия деятельности фирмы и выбор стратегии (конкуренция, прибыль, ценообразование, налоги);

- систему обеспечения и обслуживания, от которой зависит уровень обслуживания и наличие запасных частей в ремонтных мастерских.

Задача № 26. Процесс сборки изделия (автомобиля, прибора и т.п.) можно рас-сматривать как систему, элементами которой являются отдельные операции. Их взаимосвязь представлена матрицей инциденций, приведенной в таблице. По данным таблицы постройте уровни порядка следования операций по очередности. Итоговый результат представьте в виде порядкового графа.

Таб.2 Исходные данные

Операции	O1	O3	O4	O5	O7	O8	O9	O10	O11	O12	O13
O1		1									1
O3
O4		1
O5		1					1	1
O7									1
O8			1		1
O9	1
O10	1				1					1
O11		1
O12
O13		1

Решение

Определим систему в виде S = {х ; R}, где х – множество автомобилей, R - отношение порядка.

Шаг1.

Составим векторную строку А0, равную сумме строк исходной матрицы

А0 = {25102011111}

Нули в строке А0 дают операции, которые предшествуют другим.

В нашем случае это операции (О5, О8) – они образуют первый порядковый уровень N0 – первый порядковый уровень.

Шаг 2.

Преобразуем строку А0 следующим образом: нули заменим знаком х, исключим из строки значения, соответствующие нулевым операциям, для чего зачеркнем одинаковым способом строки О5 и О8

В итоге получим строку А1 = {240х1х00111}

Новые нули в строке А1 дают элементы: О4,О9,О10, они образуют порядковый уровень N1.

Шаг3.

Преобразуем строку А1, исключая значения, соответствующие нулевым элементам, и заменяя предыдущие нули крестом.

В итоге получим строку А2={03хх0ххх101}. Появившиеся новые нули соответствуют элементам О1, О7,О12 образующему N2 порядковый уровень.

Шаг 4.

Преобразуем строку А2, исключая значения, соответствующие нулевым элементам, и заменяя предыдущие нули крестом, в итоге получим строку А3= {х2хххххх0х0}. Появившиеся нули соответствуют О11 и О13 элементам, образующую N3 порядковый уровень.

Шаг 5.

Преобразуем строку А3, исключая значения, соответствующие нулевым элементам, получим строку А4= {х0ххххххххх}, появившиеся нули соответствую – O3 элементу, образуя- N4 порядковый уровень.

Результаты показывают, что элементы множества располагаются по уровням порядка следующим образом: N0- {O5, О8}, N1 – { О4,О9,О10}, N2 – { О1, О7,О12 }, N3 – { О11,О13}, N4 – {О3}

Задача № 28. По результатам испытаний приборостроительной продукции бы-ли выявлены типовые причины неисправностей и проведено их ранжирование по ряду признаков. Соответствующая матрица инциденций дана в таблице. Постройте уровни порядка на множестве неисправностей по отношению предпочтения («не менее важен, чем»). Итоговый результат представьте в виде порядкового графа. Дайте возможную интерпретацию полученных результатов.

Таб. 3 Исходные данные

Неисправности	x1	x3	x4	x5	x7	x8	x9	x10	x11
x1	1				1
x3		1	1				1	1
x4			1	1
x5			1	1
x7					1				1
x8						1
x9		1					1
x10	1		1	1			1	1
x11	1			1					1

Решение:

Построим диагностическую систему S={x, R}, где элементы множества x – являются неисправности x={X1, X2…….X10} множество причин неисправностей.

Зададим отношение R – отношение предподчтения.

Причина хi не менее важна, чем хj.

В этой строке А0 не содержит нулей, т.е. в матрице имеются циклы. Нужно объединить элементы, связанные циклом в группы эквивалентности.

Строка1

Исходный элемент х1 связан сам с собой и с х7. Смотрим строку х7. Наша цель – установить, если ли обратный путь из х7 в х1. Элемент х7 связан сам собой и с х11. Смотрим элемент х11, который связан сам собой, с х7, х6, х1 (получаем цикл).

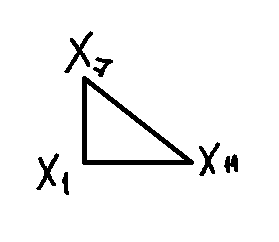
С1

Строка 2

Исходный элемент х3, связан сам с собой с х4, х9 и х10. Элемент х4 связан сам с собой и х5 путь к х3 не ведет, х9 связан сам с собой и с х3(возврат в х3). Элемент х10 связан сам с собой и с х4, х5, х9 и х1 путь к х3 ведет через х9 (цикл).

Строка 3

Исходный элемент х4 связан сам с собой и с х5, элемент х5 связан сам с собой и с х4 (возврат к х4)

Элемент х5 не рассматривается, так как вошел в С3.

Элемент х7 вошел в С1. Исходный элемент х8 – автоцикл. (С4)

Элемент х9 вошел в С2.

Х10 – вошел в С2.

Х11 – вошел в С1.

Наша матрица содержит 4 класса эквивалентности.

Преобразуем исходную матрицу, используя информацию о циклах. Заменим в матрице единицы на нули для всех элементов, попавших в один и тот же класс эквивалентности.

Неисправности	x1	x3	x4	x5	x7	x8	x9	x10	x11
x1	0				1
x3		0	1				0	1
x4			0	0
x5			0	0
x7					0				1
x8						0
x9		0					0
x10	1		1	1			1	0
x11	1			1					0

Преобразованная матрица циклов не содержит, применим к ней метод, рассмотренный в предыдущей задаче, образуем строку А0.

А0={202210111}

Выпишем нулевые элементы: х3х7х8 – N0

Шаг 2

Преобразуем строку А0. Получим А1={2х121х100}

Выпишем нулевые элементы: х10, х11 –N1

Шаг 3

Преобразуем строку А1, получим строку А2 = {0х001х0хх }

Выпишем нулевые элементы: х1х4х5х9 – N2

Шаг 4.

Преобразуем строку А2 – получим А3 = {х х х х 0 х х х х}

Выпишем элемент х7 – N3

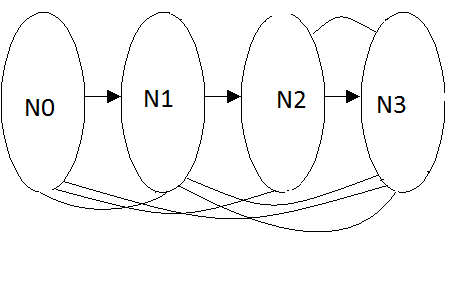
Задача № 76. По данным приведенной ниже таблицы определите наилучший вариант решения, используя следующие методы: аддитивная свертка, мультипликативная свертка, свертка по наихудшему критерию, свертка по наилучшему критерию, метод главного критерия. Задачу решите для двух случаев: а) важность критериев одинакова; б) важность критериев составляет соответственно a1 = 0,26, a2 = 0,21, a3 = 0,15, a4 = 0,18.

Варианты	K1	K2	K3	K4	K5
B1	4	4	3	3	5
B2	3	4	3	4	4
B3	4	5	3	2	4
B4	4	4	5	3	5
B5	4	4	4	4	4
B6	5	3	4	4	3
B7	2	4	3	5	4

Решение:

По первому варианту: