5.8 Задачи по разделу 5
Пример 1. В дискретном канале без помех для передачи сообщений используется алфавит с четырьмя различными символами. Длительность всех символов одинакова и равна 1 мс. Определить пропускную способность канала передачи информации.
Решение.
Запишем выражение для пропускной способности дискретного канала без помех:
,
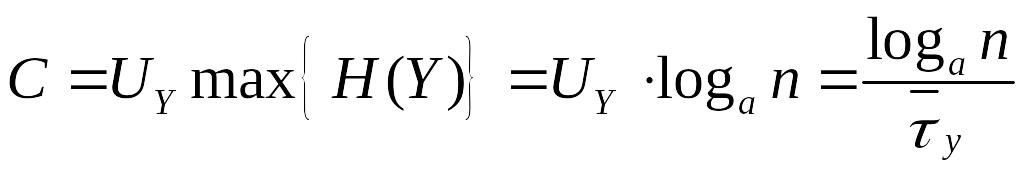n – общее количество сообщений из алфавита с четырьмя символами.
n=44=64;
мс.
дв.ед/с.
Пример 2. Источник вырабатывает символы с вероятностями р1=0,2; р2=0,7; р3=0,1. Передача информации осуществляется двоичным кодом, длительность всех символов которого равна 1 мс. Определить скорость передачи информации по каналу без помех при использовании равномерного кода.
Решение.
Запишем выражение для скорости передачи информации:
,
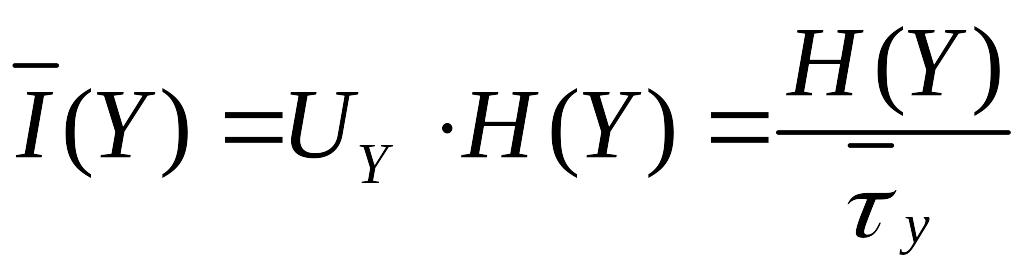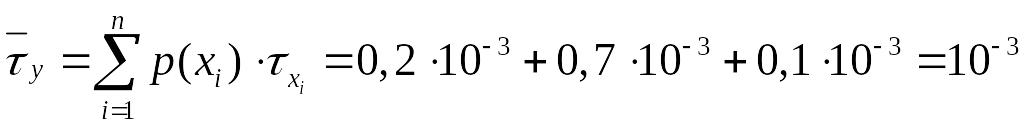
дв.ед/с.
Пример 3. Источник, вырабатывающий четыре символа с априорными вероятностями р1=0,4; р2=0,3; р3=0,2; р4=0,1, подключен к каналу передачи информации, обладающим пропускной способностью С=1000 бит/сек. Передача информации осуществляется равномерным двоичным кодом. Определить скорость передачи информации.
Решение.
Выражение для скорости передачи информации имеет вид:
,
Выразим UY из выражения пропускной способности канала связи:
;
бит/с.
бит.
бит/с.
Пример 4. Сколько в среднем можно передать букв русского текста за 1 сек по каналу передачи информации, обладающего пропускной способностью С=1000бит/с, при условии, что средняя энтропия русского языка на одну букву – 2бит. Определить количество информации.
Решение.
;
Выразим UY из выражения пропускной способности канала связи:
, поскольку n=32 (количество букв в русском алфавите), то
бит/с,
Н(Х)=2
бит,
бит/с.
Пример 5. Определить пропускную способность двоичного симметричного канала с помехами при вероятностях искажения элементарного символа q=0,001 и q=0,01.
Решение.
1) q=0,001, р=1-q=1-0,001=0,999;
бит/с.
2) q=0,01, р=1-q=1-0,01=0,99;
бит/с.
Пример 6. Определить энтропию системы, которая описывается дискретной случайной величиной х со следующим рядом распределения: р(х1)= р(х2)= р(х3)= р(х4)=0,01, р(х5)=0,96.
Решение.
Запишем выражение для энтропии дискретной случайной величины:
бит.
Пример 7. Определить энтропию системы, которая описывается дискретной случайной величиной хi со следующим рядом распределения р(х1)= р(х2)= р(х3)= р(х4)= р(х5)=0,2.
Решение.
бит.
Пример 8. Определить отношение С/Ш на выходе системы, показанной на рисунке 5.9 с коэффициентами усиления G1 , G2 и G3, записать в числовом виде и выразить в децибелах. Мощность входного сигнала равна 2мВт, уровень шумов – 5мкВт. Предполагается, что звенья схемы не вносят собственных шумов.
Рисунок 5.9
Решение.
Определим С/Ш на
входе системы :
.
Определим С/Ш на
выходе системы :
.
Выразим отношение
С/Ш в децибелах на входе системы:
.
Выразим в децибелах коэффициенты усиления каждого звена схемы:
Отсюда общий коэффициент усиления системы будет равен:
G1 + G2 + G3=16,02+10+9,03=35,05дБ.
Отношение С/Ш в децибелах на выходе системы будет равен:
.