5.4 Скорость передачи информации и пропускная способность каналов с помехами и без помех

5.4.1 Скорость передачи информации и пропускная способность дискретного канала без помех

Под дискретным каналом связи понимается совокупность средств, предназначенных для передачи дискретных сигналов. На вход такого канала подаются дискретные сообщения, которые преобразуются в кодированные сигналы. В канале без помех каждому входному сигналу соответствует тот же сигнал на выходе, т.е. входные и выходные сигналы связаны однозначной зависимостью. В этом случае среднее количество информации, переносимое одним элементарным символом, равно энтропии символа на входе канала, т.е.

. (5.26)

Скорость передачи информации: двоичных ед./сек.,

где – скорость передачи элементарных символов сигнала;

– средняя длительность элементарных сигналов.

Пропускная способность канала равна: .

Полагая, что задана, максимальная скорость передачи информации будет обеспечена при максимальном значении энтропии кодированного сигнала:

. (5.27)

Таким образом, скорость передачи информации может быть максимальной при условии, что статистические характеристики источника сигнала согласованы со свойствами канала. Это достигается выбором способа кодирования.

5.4.2 Скорость передачи информации и пропускная способность дискретного канала связи с помехами

При наличии помех всегда нарушается соответствие между входными и выходными сообщениями. Одному входному сигналу могут соответствовать различные выходные. Из-за случайного характера помех можно говорить о вероятностях получения на выходе канала элементарного сигнала при условии, что отправлен сигнал . Вероятностный характер связи между входными и выходными сообщениями определяется матрицей переходных вероятностей:

(5.28)

где – условная вероятность перехода -го символа входного сообщения в символ выходного, причем , при .

Рассмотрим бинарный канал, по которому передаются только два элементарных сигнала, обозначенных для определенности через 0 и 1. Матрица переходных вероятностей имеет вид:

. (5.29)

Если вероятности правильной передачи сигналов и вероятности искажений попарно одинаковы, то канал называется симметричным, т.е. и .

Скорость передачи информации по дискретному каналу с помехами равна:

, (5.30)

где определяется исходя из выражений для бинарного симметричного канала с помехами

и . (5.31)

Отсюда равно:

,

поскольку для бинарного канала вероятность приема символа или , т.е. 0 или 1 при передаче любого символа или , т.е. 0 или 1, равна 1.

.

Подставляя выражения для энтропий, получим формулу для скорости передачи информации:

. (5.32)

Отсюда видно, что скорость зависит от статистических характеристик источника сообщений. Максимальная скорость передачи информации наблюдается при ; – количество элементарных сигналов

бит. (5.33)

Пропускная способность бинарного симметричного канала определяется выражением:

. (5.34)

Наличие помех уменьшает пропускную способность канала, т.к. в канале без помех пропускная способность имела бы вид:

. (5.35)

5.4.3 Скорость передачи информации и пропускная способность непрерывного канала связи с помехами

Под непрерывным каналом передачи информации понимается совокупность средств, предназначенных для передачи непрерывных сигналов. Для описания непрерывных сигналов используются средние статистические характеристики: среднее значение случайной величины, или математическое ожидание, дисперсия, т.е. мера разброса случайной величины относительно среднего значения, корреляционная функция – это степень взаимной зависимости случайных значений процесса в разные моменты времени, функция плотности распределения вероятности и интегральная функция распределения вероятности.

Одной из основных характеристик является одномерная функция плотности распределения вероятности – . Она показывает вероятность появления того или иного значения случайного процесса.

На рисунке 5.7, а указаны уровни анализа от до х+∆х, а на рисунке 5.7,б показано определение вероятности попадания значения случайного процесса n(t) в интервал ∆х, т.е.

, (5.36)

где – интервалы времени, при которых функция n(t) находится в интервале ∆х; – интервал наблюдения.

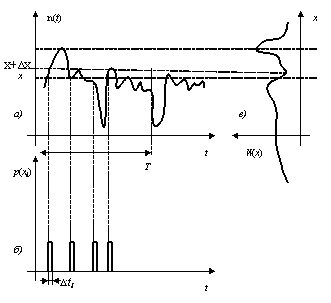
Рисунок 5.7 – Графическое представление а) случайного процесса n(t); б)

интервал нахождения n(t) в интервале ∆х ; в) функция

плотности распределения вероятности .

Данная вероятность зависит от ∆х. Чтобы исключить такую зависимость необходимо разделить вероятность (5.36) на ∆х и выполнить предельный переход:

(5.37)

Таким образом, одномерная функция плотности распределения вероятности есть предел отношения вероятности попадания значений случайного процесса в интервал ∆х к ширине этого интервала при условии ∆х→0.

Свойства функции плотности вероятности :

1) вероятность того, что случайный процесс n(t) лежит в интервале , равна 1.

.

В непрерывных каналах вместо кодирующих и декодирующих устройств может использоваться более широкий класс преобразователей. Для передачи информации по такому каналу может применяться модуляция одного или нескольких параметров сигнала. Входные и выходные сигналы непрерывного канала задаются в виде ансамбля непрерывных функций с соответствующими плотностями распределения вероятностей;

2) вероятность попадания значений случайного процесса в интервал {a,b}:

(5.38)

3) вероятность при равномерном виде : .

Скорость передачи информации принимает вид:

, (5.39)

где Т_к – интервал временной дискретизации;

h(Z) – дифференциальная энтропия одного отсчета;

h(Z/Y) – условная дифференциальная энтропия данного отсчета.

Пропускная способность непрерывного канала связи с помехами имеет вид:

. (5.40)