3.3 Задачи по разделу 3

Пример 1. Представить ряд Фурье и определить спектр периодического сигнала, представленного на рисунке 3.12, имеющего амплитуду h, период Т₀ и длительность импульсов τ.

Рисунок 3.12 – Периодический сигнал

1) Подставляем исходные данные в выражение комплексной амплитуды частоты спектра (3.15):

;

Используя табличный интеграл , получим :

Таким образом, частотный спектр периодической последовательности прямоугольных импульсов в виде ряда Фурье запишется как:

. (3.27)

Из (3.27) следует, что огибающая амплитудного спектра соответствует амплитуде спектра одиночного импульса (3.16). Эта огибающая изображена штриховой линией на рисунке 3.13.

2) Для определения спектральных составляющих a_k и b_k воспользуемся выражением (3.4). Из графика видно, что среднее значение функции или постоянная составляющая сигнала а₀ = 0 В. Запишем выражение для функции S(t) на длине одного периода Т :

Определим косинусоидальные составляющие ряда Фурье:

Поскольку T=2π/ω, то sinkωT=sink2π=0, поэтому это выражение можно записать как:

Отсюда

Теперь определим синусоидальные составляющие сигнала:

где , следовательно , . Таким образом, спектр данного сигнала имеет только косинусоидальные составляющие, синусоидальные составляющие равны нулю, отсутствует и постоянная составляющая. Присутствуют только косинусоидальные составляющие только нечетных гармоник.

В итоге выражение для функции S(t) согласно (3.8) принимает следующий вид:

Спектр этого сигнала представлен на рисунке 3.13.

Рисунок 3.13 – Частотный спектр периодической импульсной последовательности

Пример 2. Найти спектр амплитуд периодической последовательности импульсов с амплитудой U=10B, периодом T₀=10мс и длительностью τ=5мс.

Решение.

1. Запишем формулу для спектра амплитуд:

2. Подставим заданные значения:

где – номера гармоник; .

3. По формуле определим значения для :

; ; ;

C₀=5В; 3,2В;

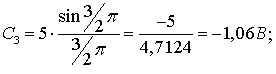
4. Определяем частоту ω₀:

Рисунок 3.14

Пример 3. Осуществить восстановление исходного сигнала по его спектру, используя для восстановления постоянную составляющую S₀ =10 B гармоники со значениями комплексных амплитуд S₁=5B, S₂=0B, S₃=-1,06B, S₄=0B. Частота первой гармоники

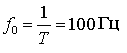
Суммирование членов ряда Фурье при восстановлении осуществить графическим методом. Оценить качество восстановления исходного сигнала при использовании только постоянной составляющей, постоянной составляющей и первой гармоники, постоянной составляющей и всех гармоник.

Решение. Используя ряд Фурье (3.5), имеем:

.

а) при восстановлении исходного сигнала по постоянной составляющей имеем (т.к. по ):

Рисунок 3.15

б) при восстановлении исходного сигнала по сумме S₀+ S₁ имеем

– не существенно.

Строим график (рисунок 3.16):

при	t=0мс	; ; ; ; ( )
	t=±2,5мс
	t=±5мс

Рисунок 3.16

в) при восстановлении по сумме

Строим график:

при
	t=2,5мс
	t=5мс

Рисунок 3.17

Вывод: При большем числе гармоник результат восстановления получается лучше. При точном подсчете при использовании десяти гармоник сигнал принимает исходный вид.

Пример 4. Найти спектр –функции, исходя из спектра одиночного прямоугольного импульса длительностью и амплитудой , при . Изобразить график .

Решение.

1. Запишем выражение для спектра одиночного прямоугольного импульса (3.16):

;

2. Подставим значение .

;

3. Возьмем предел от функции при условии, что

Рисунок 3.18 – Амплитудный спектр δ–функции

Пример 5. Исходя из выражения для спектра амплитуд последовательности прямоугольных импульсов найти спектр постоянного сигнала S(t)=h. При решении использовать условие преобразования периодической последовательности прямоугольных импульсов в постоянный сигнал, т.е. .

Решение.

1. При

Рисунок 3.19

2. Воспользуемся выражением для спектра амплитуд последовательности прямоугольных импульсов (3.27). При этом, периодическая последовательность прямоугольных импульсов рядом Фурье запишется как:

.

3. Возьмем предел от 3.27:

=h.

Пример 6. Вычислить спектр одиночного экспоненциального импульса:

, где – некоторая постоянная.

Изобразить график экспоненциального импульса и модуля его спектральной плотности.

Решение.

1. Используя прямое преобразование Фурье, имеем:

2. Изобразим график экспоненциального импульса.

Рисунок 3.20 – Экспоненциальный импульс

Найдем модуль спектральной плотности (рисунок 3.21).

;

;

Рисунок 3.21 – Частотный спектр экспоненциального импульса

При ;

;

.

Пример 7. Исходя из выражения для спектра одиночного экспоненциального импульса найти спектр сигнала включения:

.

Изобразить график сигнала включения и модуля его спектральной плотности.

Решение.

1. Запишем спектр одиночного экспоненциального импульса:

Поскольку β=0, то выражение для сигнала включения имеет вид:

2. Изобразим график сигнала включения:

Рисунок 3.22 – Сигнал включения

3. Модуль спектральной плотности сигнала включения – амплитудный спектр.

.

4. График модуля спектральной плотности.

Рисунок 3.23 – Частотный спектр функции включения

при ;

.

Пример 8. Найти представление сигнала во временной области, используя обратное преобразование Фурье.

Решение.

1) Запишем обратное преобразование Фурье:

.

2) Подставим значение функции S(t) и учтем, что ω=2πf, получим выражение:

Пусть левый интеграл уравнения равен I₁ а правый I₂. Тогда , где

Таким образом, функция принимает вид:

. То есть получается прямоугольный импульс.

Пример 9. Дана функция S(t), график которой приведен на рисунке 3.24. определить вид функции S(t/3+2).

Рисунок 3.24

Решение.

Функция масштабируется S(t) масштабируется с коэффициентом 3 и сдвигается влево на 2 единицы. Сначала можно применить операцию масштабирования, после которой получим график (рисунок 3.25):

Рисунок 3.25

Применив операцию сдвига на 2 получим искомую функцию (рисунок 3.26).

Рисунок 3.26

Таким образом, наличие коэффициента у аргумента функции, описывающей сигнал (t/3) приводит к масштабированию, а наличие суммирования с постоянным коэффициентом (+2) приводит к сдвигу, если со знаком «+», то влево, если «-», то вправо.