3.1.3 Частотный спектр непериодического сигнала

Рядом Фурье вида (3.3) или (3.12) могут быть представлены только периодические сигналы. Но строго периодических сигналов не бывает, т.к. сигналы имеют начало и конец, изменяют свою форму в связи с модуляцией, действием помех. Всякий непериодический сигнал (неповторяющийся, однократный) можно рассматривать как периодический, период которого равен , т.е. T₀ → ∞.

Рисунок 3.4 - Непериодический сигнал

При увеличении периода T₀ интервалы между частотами гармонических составляющих в спектре сигнала и амплитуды спектральных составляющих уменьшаются и в пределе, при T₀→ ∞, становятся бесконечно малыми величинами (3.2). При этом ряд Фурье, представляющий спектральное разложение периодического сигнала, преобразуется в интеграл Фурье, отображающий спектральное разложение непериодического сигнала.

Рассмотрим, как произойдут эти изменения. Для этого в ряд Фурье (3.12) и в выражение (3.13) введем

,

Из выражения (3.2) следует, что kω₀ = k2π/T₀ и превращается в текущее значение частоты при T₀→∞, т.е. kω₀→ω,тогда пределом интеграла F является некоторая функция частоты:

(3.14)

Данная функция имеет смысл спектральной плотности комплексной амплитуды. Комплексные амплитуды при T=∞ становятся бесконечно малыми:

.

В связи с этим в выражении для ряда Фурье сумма может быть заменена интегралом Фурье. В результате получается прямое и обратное преобразование Фурье:

	– для вычисления спектральной плотности амплитуды	(3.15)
	– для восстановления исходного сигнала по спектру

Примеры непериодического сигнала:

1. Прямоугольный импульс

Аналитическое выражение: Временное представление:

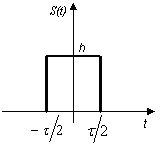
Рисунок 3.5 – Прямоугольный импульс

Для определения спектральной плотности амплитуд прямоугольного импульса воспользуемся интегралом Фурье (3.13) и формулой Эйлера (3.6)

(3.16)

Из (3.16) следует, что спектральная плотность амплитуды прямоугольного импульса описывается функцией вида . Из математики известно, что . На рисунке 3.6 представлен график зависимости (3.16). Определим ширину спектра прямоугольного импульса ∆ω_пр, для чего определим значения частот, в которых наблюдается первый ноль, т.е. определим корни уравнения Ф(ω)=0. Выражение (3.16) обращается в ноль при значениях аргумента синуса кратных π: , при n=±1.

Откуда и или . (3.17)

Из (3.17) следует, чем короче прямоугольный импульс, тем шире его спектр. В этом частном случае проявляется фундаментальное свойство преобразования Фурье: длительность сигнала и ширина его частотного спектра связаны обратно пропорциональной зависимостью.

Рисунок 3.6 – Амплитудный спектр прямоугольных импульсов

2) Дельта функция – δ(t) – это математическая (абстрактная) модель сигнала.

Аналитическое выражение

При этом

Рисунок 3.7 - Временное представление δ - функции

Спектральная плотность амплитуды: Ф(ω)=1. Дельта функция имеет сплошной бесконечно широкий спектр с постоянной спектральной плотностью.

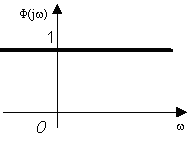
Рисунок 3.8 - Спектральное представление δ-функции