3. Построение математической модели вентильного электропривода.

Составим на основе структурной схемы рис.6а.

Рассматриваем напряжение на выходе сумматоров:

e₁ (S)= U₃(S)-K_ос(S);

T_wSl₂(S)=(T₁S+1) e₁ (S);

l₃(S)=K_i[l₂(S)-K_Ti(S)];

l₄(S)=[ l₂(S)-K_Ti(S)]K_i-C_e(S); (1)

l₄(S)= l₃(S)- l(S);

R_э(T_эS+1)I(S)= l₄(S);

S(S)= (S);

Уравнение движения ротора

I_S(S)=M_дв(S)-M_с(S); т.к. М_дв=С_мI(S), то

I_S(S)= С_мI(S)-M_тр- M_р(S)-;

Система уравнений (1), записанная в операторной форме для нулевых начальных условий сводим к одной переменной. Все уравнения вводим в уравнение движения ротора.

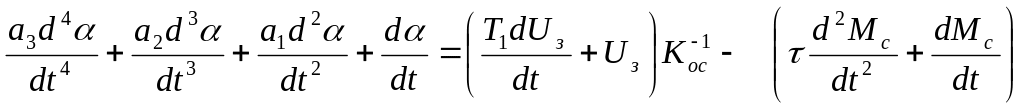(2)

Запишем значения введенных обозначений в уравнение (2):

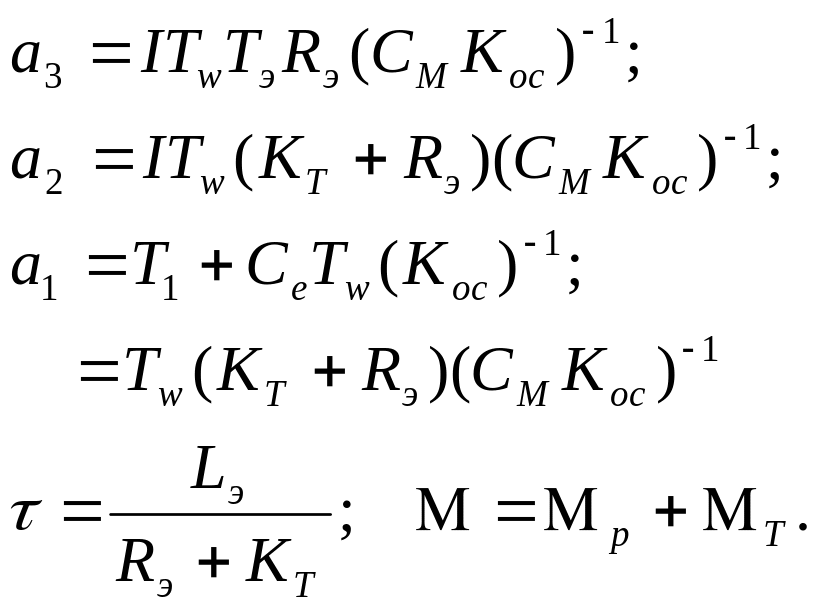(3)

Уравнение по току в операторном виде:

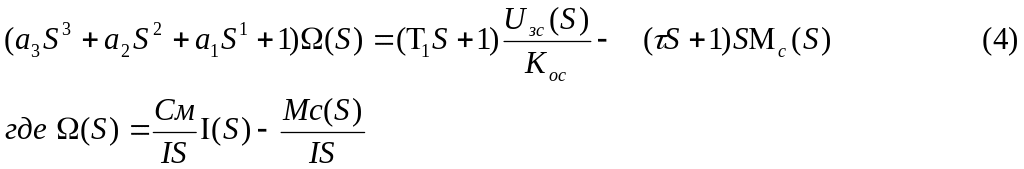
Запишем уравнение по углу:

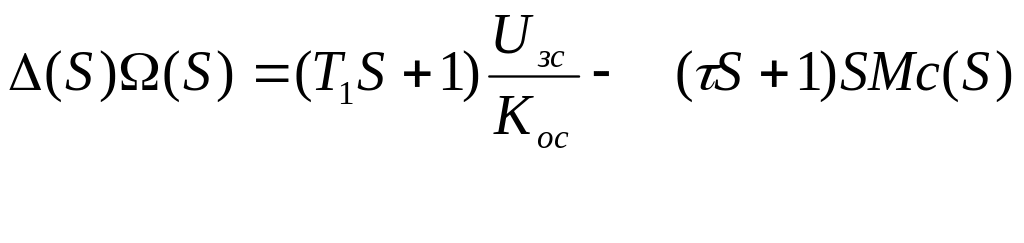
Для уравнения по току определим:

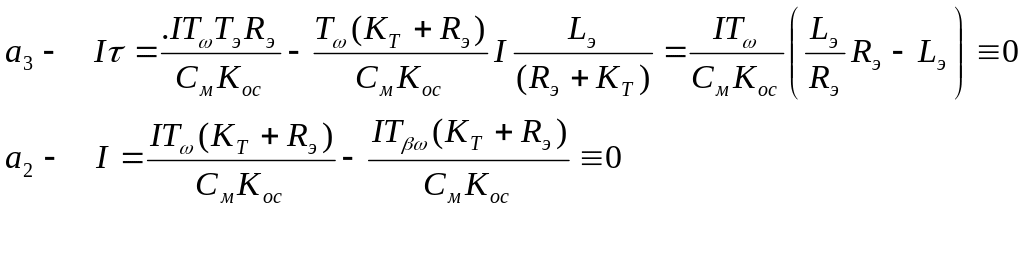
Таким образом, уравнения упрощаются и примут вид:

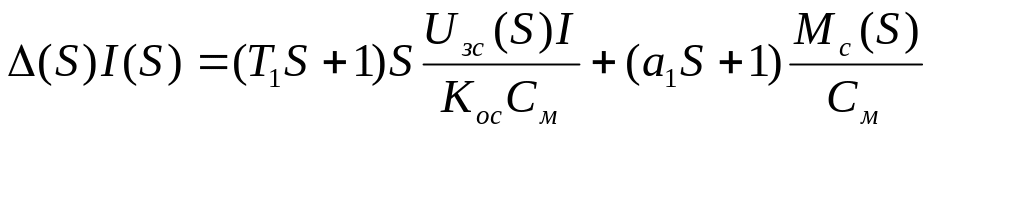
Из данных уравнений следует:

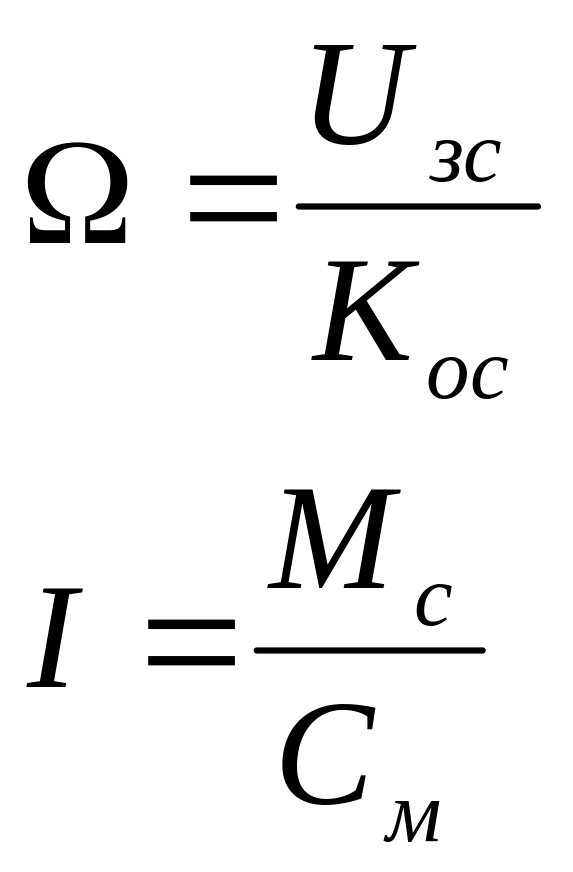
Из уравнений видно, что угловая скорость вращения ротора вала электропривода пропорциональна U_зс, т.е. она не зависит от момента сопротивления на валу. Ток в обмотке статора пропорционален моменту сопротивления и на него влияет программный ток заданного напряжения.

4. РАСЧЕТ ПАРАМЕТРОВ МАТЕМАТИЧЕСКОЙ МОДЕЛИ. ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ.

Как было выведено ранее:

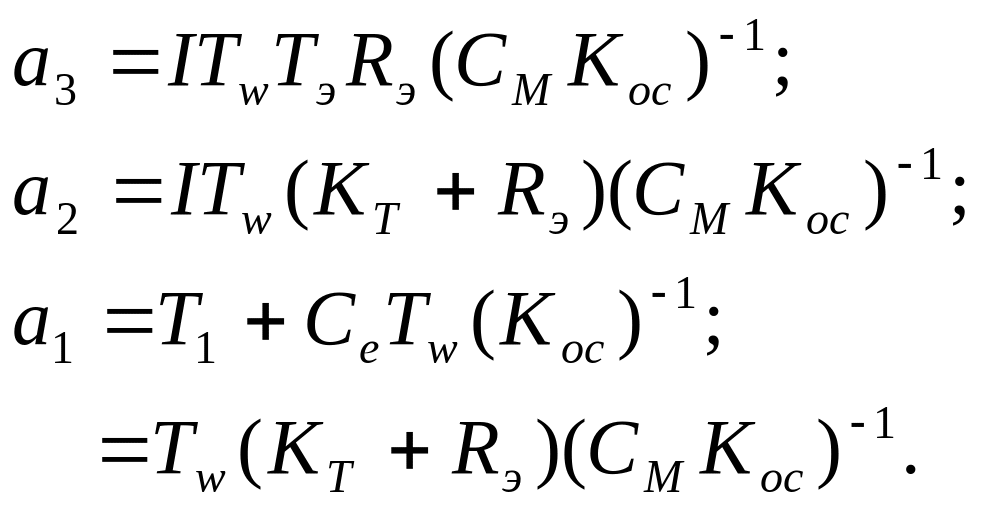
C_M=0.205 Hm/A; C_e=0.205 Bc/рад; I=0.810^-4кгм²; K_oc=2,310^-2 Bc/рад;

K_T=0.27 Om; R_э=0.52 Om; K_i=1,3; T_w=1.5210^-3 c; T₁=2.810^-3 c; U_з=0,1;1;10 B;

_э=0.6510^-3 Гн.

Отсюда находим:

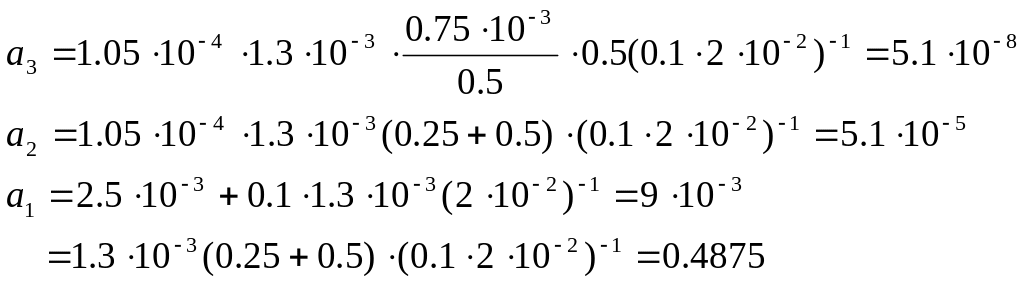
Исследование устойчивости нелинейной системы осуществляется методом Гурвинца. Вначале будем пренебрегать моментами, примем M_р=M_Т=0, тогда уравнение примет вид:

, Получили линейное уравнение с постоянными коэффициентами на основе критерия Гурвинца:

910^-35.110^-5>5.110^-8 . По критерию Лебедева, если неравенство выполняется, то обеспечен большой запас устойчивости.

Видно, что обеспечена устойчивость.

Запишем уравнение движения по угловой скорости с учетом коэффициентов:

Запишем уравнение по току с учетом коэффициентов:

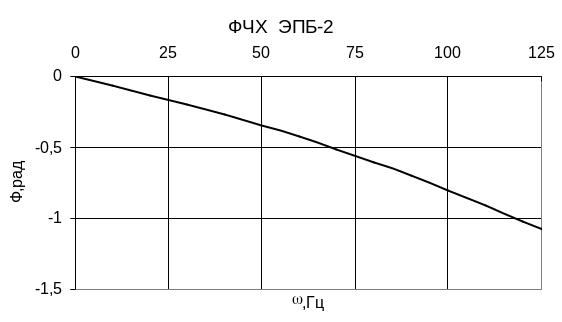
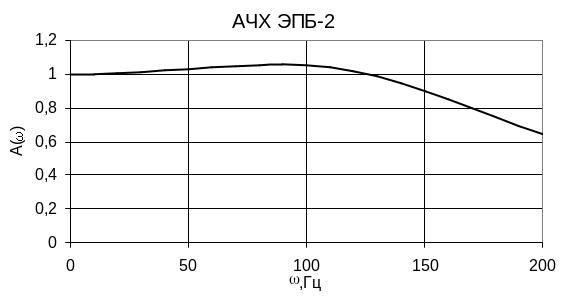
5. Расчет и построение ачх и фчх эп.

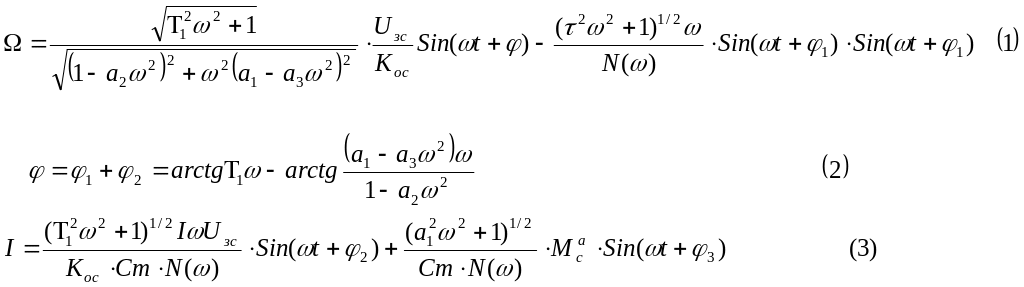
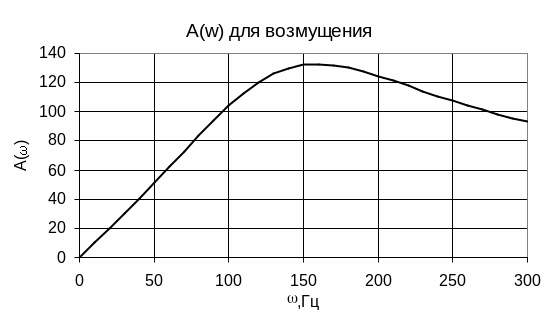
(1)-амплитудная частотная характеристика ЭП.

(2)-фазовая частотная характеристика ЭП.

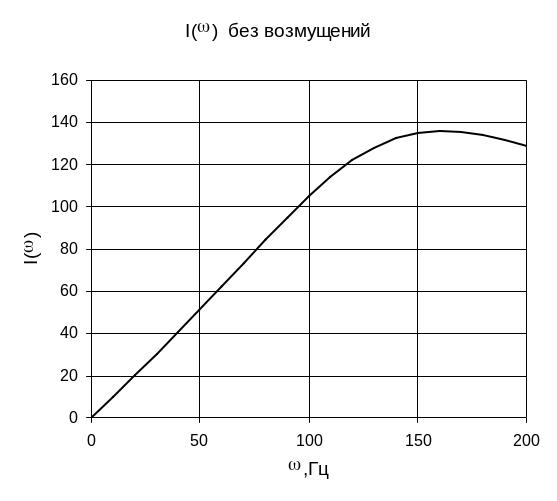
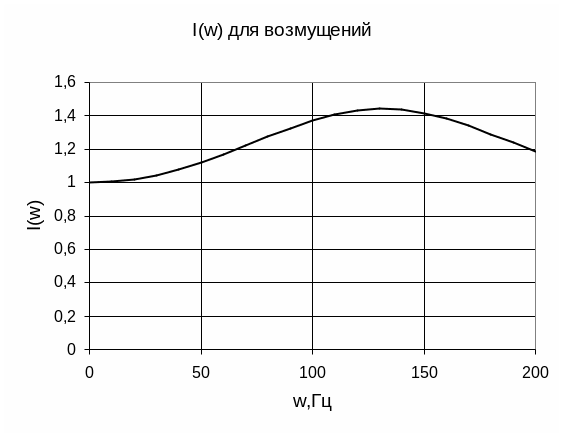
(3)-зависимость тока от частоты.

6. Расчет момента трения.

По заданным d_в=10мм, выбираем подшипник С6101Е.

d_ш=0,4763 cм,d_в.п=1,2 см.

P=1.1+0.1n- вес ротора (радиальная нагрузка)

Р=1.4кг F_r=Pg=1.410=14H.

Момент трения вычисляется по формуле:

где F_r-радиальная нагрузка; d_в.п-диаметр внутреннего кольца шарикоподшипника; d_ш-диаметр шарика; Р_ц-дополнительное усилие от центробежных сил действующих на шарик; -коэффициент трения качения.

При малых оборотах Р_ц=0, момент можно выразить по упрощенной формуле:

F_r=14 H; =0,0003 см;

Так как в электродвигателе установленны два одинаковых шарикоподшипника, то полный момент трения необходимо удвоить.

М_тр.п=2М_Тр=20.018=0.036 (Нсм).

7.Расчет параметров переходного процесса с помощью эвм.

Уравнение движения ЭП при М=0 имеет вид:

Система имеет решение:

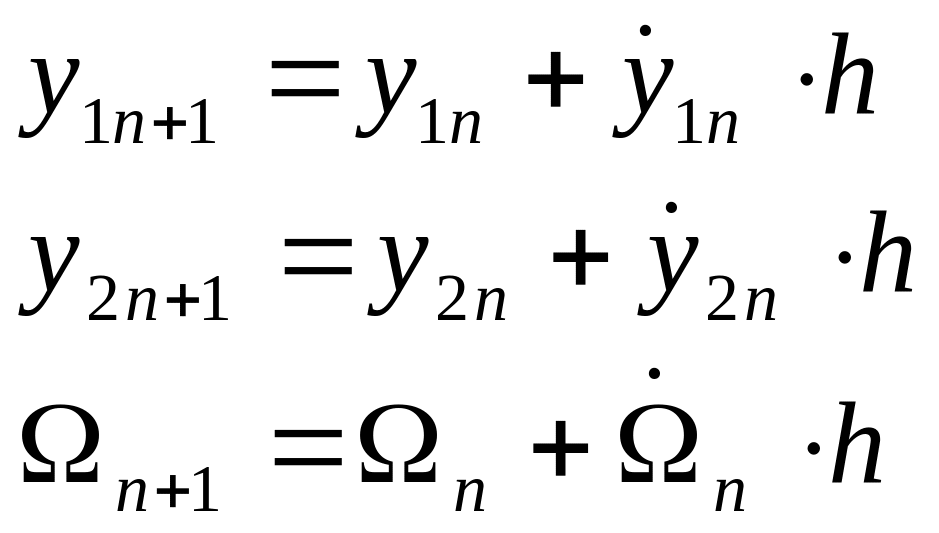,следовательно,

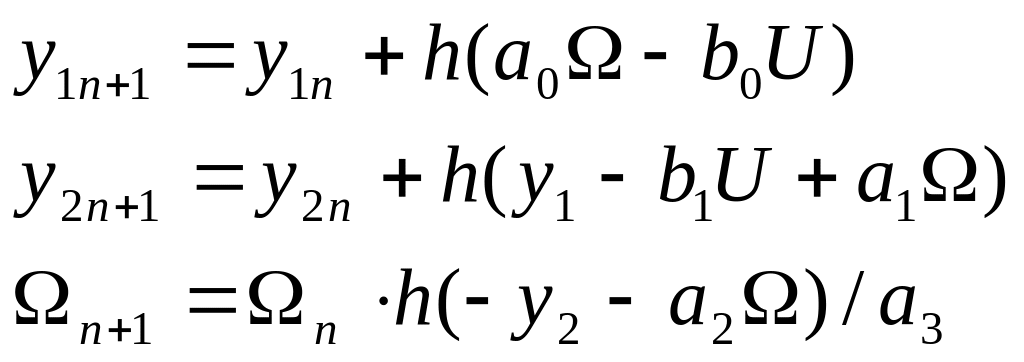
h-шаг интегрирования. Можно с помощью моделирования вычислить значения угла поворота  :

Моделирование производится с помощью табличного процессора Excel.

Графики переходного процесса при U_з=0,1 В

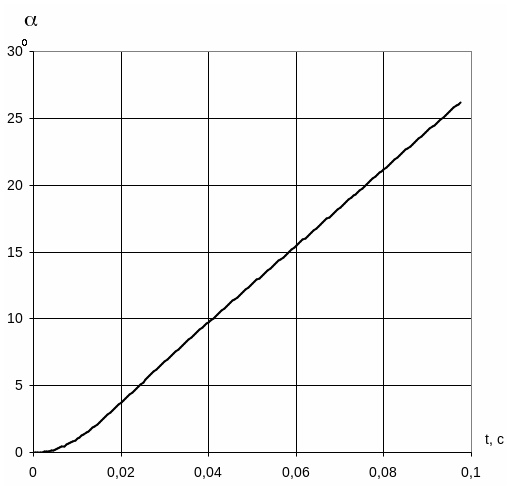
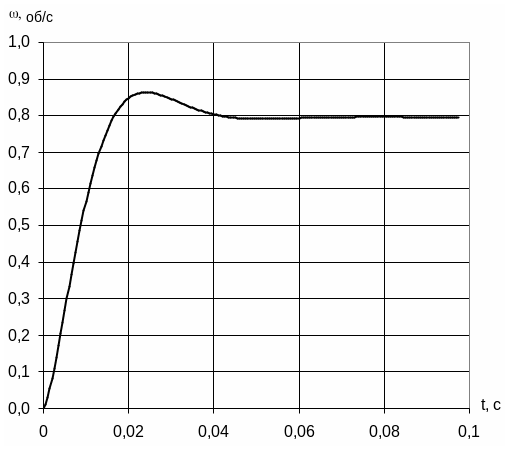
Графики переходного процесса при U_з=1В

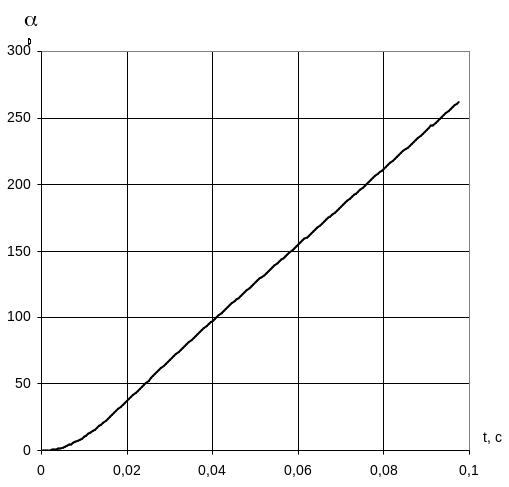
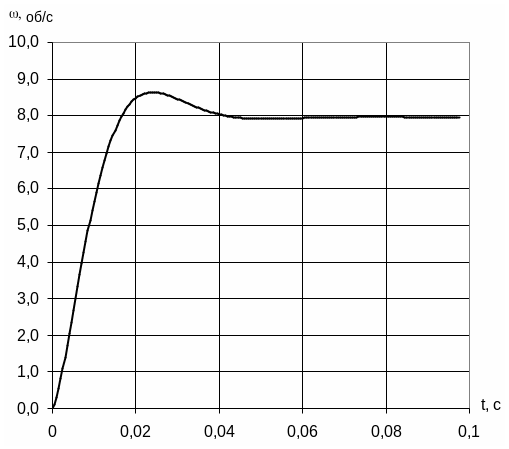
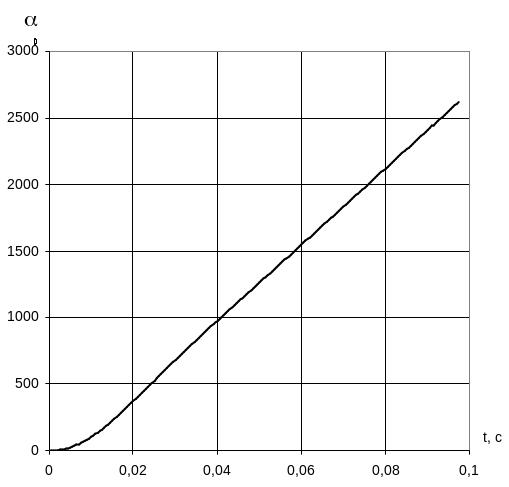
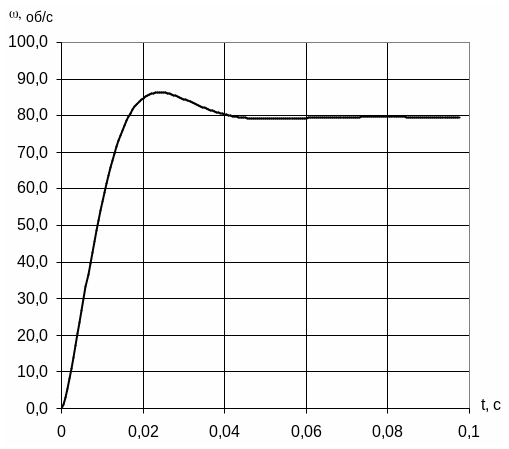
Графики переходного процесса при U_з=10 В

Р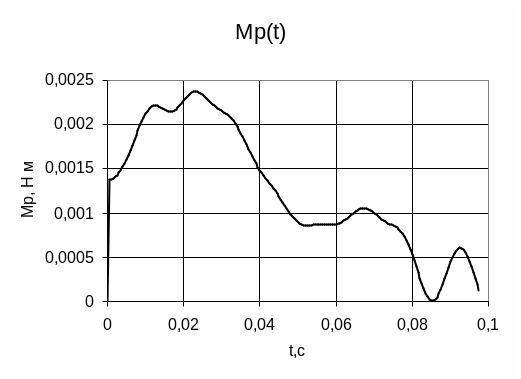 еактивный момент при U=0.1В

Р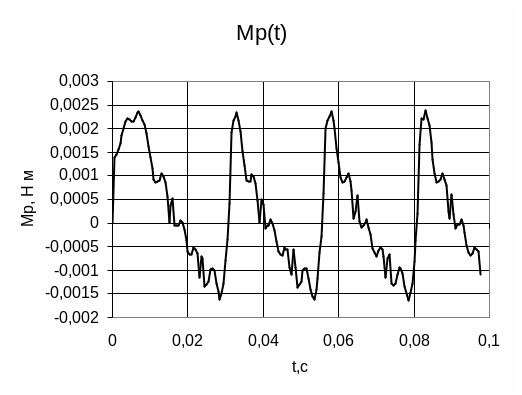 еактивный момент при U=1B

Реактивный момент при U=10B