Тема: Функции нескольких переменных (фнп)
Дифференциальное исчисление функций многих переменных.
1. Частные производные.
1.Примеры.
В разделах дифференциального и интегрального исчислений мы имеем дело с функциями одной переменной. На практике часто приходится иметь дело с функциями двух, трех и большего числа переменных. Такие функции называются функциями многих переменных. Примером такой функции является производственная функция Кобба-Дугласа
где
есть величина выпуска продукции, а
и
обозначают объемы затраченных ресурсов
труда и капитала соответственно. В
экономических задачах функцию
Кобба-Дугласа двух переменных в общем
виде записывают следующим образом:
,
где
есть положительные константы такие,
что
,
а
есть затраченные ресурсы труда и капитала
соответственно.
Приведем
еще примеры функций
и
переменных:
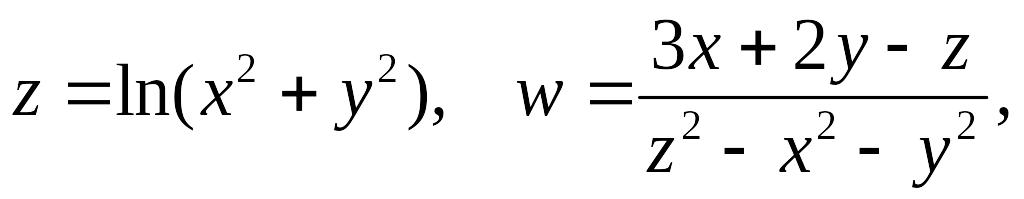
2.
-мерное
пространство Rn
.
Определение.
Пусть
.
Будем называть Rn
следующее множество упорядоченных
наборов действительных чисел:
Сами
упорядоченные наборы
будем называть точками
,
а числа
,
где
,
будем называть координатами этой точки.
Часто
для удобства точки Rn
будем
обозначать так:
или
или
или
и т. д.
В
пространстве Rn
вводится
расстояние между точками
по формуле
(1)
Замечание.
При
и
равенство (1) представляет известные
формулы расстояния между точками на
плоскости и в пространстве.
Приведем без доказательства основные свойства расстояния в Rn:
1)
2)
3)
Замечание.
Пространство Rn
можно рассматривать и как векторное
пространство. В этом случае упорядоченный
набор чисел
называется вектором пространства Rn.
Векторы обычно обозначают строчными
латинскими буквами:
или
,
или другими буквами. Нулевым вектором
называют вектор
В
векторном пространстве Rn
вводятся
операции сложения векторов и умножения
векторов на число. Пусть
и
Тогда
1)
2)
Векторное пространство Rn с операциями сложения и умножения на число называют также линейным или евклидовым пространством.
Определение. Длиной или нормой вектора называется число
Для нормы вектора справедливы следующие свойства:
1)
2)
3)
Определение.
Скалярным
произведением векторов
и
называют выражение
Не трудно доказать следующие свойства скалярного произведения:
1)
2)
3)
4)
Определение.
Пусть
Функцией
переменных называется отображенные
Значение функции
записывается
в виде
где
При
этом множество
называется областью определения функции
и обозначается
Замечание.
Функцию
n
переменных можно записывать в привычном
виде
где
